Osservato che l’insieme H di base [0, 1] è normale rispetto ad y si può spezzare in due integrali semplici, e si ha: \[\iint_{H}^{} xdxdy=\int_{0}^{1}dy\int_{0}^{\sqrt{y}}xdx=\int_{0}^{1}dy\left [ \frac{1}{2}x^{2} \right ]_{0}^{\sqrt{y}}=\int_{0}^{1}dy\left ( \frac{1}{2}y \right )=\frac{1}{2}\int_{0}^{1}ydy=\frac{1}{2}\left [ \frac{1}{2}y^{2} \right ]_{0}^{1}=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}\]
Esempio 2.- Calcolare il seguente integrale doppio:\[\iint_{D}^{}\frac{arctan\sqrt{x^{2}+y^{2}}}{1+x^{2}+y^{2}}\cdot \frac{1}{y}dxdy\]
con D definito come in figura 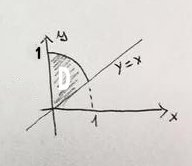
Trasformiamo a coordinate polari con le relazioni \[x=\rho\, cos\, \theta ,\, \, \, \, y=\rho\, sen\, \theta\] e si ha\[\iint_{T}^{} \frac{arctan\, \rho }{1+\rho ^{2}}\cdot \frac{1}{sen\theta }\, d\rho\, d\theta\]
ove T è il dominio normale definito dalle limitazioni \[0\leq \rho \leq 1,\, \, \, \frac{\pi }{4}\leq \theta \leq \frac{\pi }{2}\]
Applicando la formula di riduzione si ha \[\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{1}{sen\theta }d\theta \left [ \int_{0}^{1}\frac{arctan\rho }{1+\rho ^{2}} d\rho \right ]\] e l’integrale assegnato vale \[-\frac{\pi ^{2}}{32}ln\left ( tan\frac{\pi }{8} \right )\]
Puoi consultare altri esercizi svolti sul mio canale Youtube.
