Esempio 1.1.- Cinematica. Un uomo si trova davanti al Colosseo si sposta in linea retta di 5 metri e poi torna indietro nella posizione di partenza. Calcolare lo spostamento all’andata e al ritorno.
Risoluzione
Scegliamo il riferimento con l’Origine nel punto di partenza, posizione di partenza dell’uomo davanti al Colosseo, orientato positivamente nel verso del suo avanzamento. In tale riferimento la sua posizione $\displaystyle s_{0}=0\, m$ poi si muove in avanti di 5 metri e dunque raggiunge la posizione $\displaystyle s_{1}=+5\, m$. Quindi il suo spostamento all’andata è \[\Delta s=s_{1}-s_{0}=+5\,m -0\, m=+5\, m\]
Al ritorno lo spostamento sarà di – 5m: \[\Delta s=s_{1}-s_{0}=0m-5m=-5m\]
Esempio 1.2.- Un nuotatore impiega 28 secondi per fare i 25 metri di lunghezza di una piscina, al ritorno invece ne impiega 32 secondi. Calcolare la velocità media all’andata, al ritorno e su tutto il percorso.
Esempio 1.3.- Un’automobile si muove con una velocità di 120 km/h quando frena per 12 secondi e raggiunge una velocità di 56 km/h. Calcolare l’accelerazione media.
Esercizio 1.4.- Se la velocità media per andare da A a B è di 30 km/h la mattina, mentre la sera lungo li stesso percorso è di 20 km/h a causa del traffico, qual è la velocità media totale tenuta nel viaggio di andata e ritorno?
A) meno di 25 km/h
B) 25 km/h
C) più di 25 km/h.
Esercizio 1.5.- Un’auto viaggia a 80 km/h per una ora e mezza e poi a 120 km/h per trenta minuti. Trovare quanto tempo è durato il viaggio e quale distanza ha percorso. Inoltre stabilire la velocità media.
Risultati: 2 ore, 180 km, 90 km/h
Esercizio 1.6.- Durante una maratona, un atleta corre con velocità costante in un tratto ove vi sono due rilevamenti, collocati rispettivamente a 23,5 km e a 27,3 km dalla partenza. L’atleta transita al primo rilevamento all’istante 1 ora 34 minuti e 17 secondi e al secondo rilevamento all’istante 1 ora 49 minuti e 20 secondi. In questo tratto qual è la sua velocità media in m/s? E in km/h?
Risultati: 4,21 m/s, 15,1 km/h
Esercizio 1.7.- Alberto parte da A e si muove in linea retta verso B, Barbara parte da B e si muove in linea retta verso A ed entrambi si muovono con velocità costante e partono allo stesso istante. Si incontrano una prima volta a 700 metri da B e successivamente a 400 metri da A. Quanto è lungo AB?
Esercizio 1.8.- Corpo che cade da una certa altezza
Vedi esercizio svolto sul mio canale Youtube
Esercizio 1.9.- Un treno si muove in moto rettilineo in una data direzione a 68 km/h, un passeggero seduto vicino al finestrino vede una goccia d’acqua muoversi sul vetro del finestrino con velocità $\displaystyle v_{x}$, lungo l’asse x, uguale a -16 m/sec e velocità $\displaystyle v_{y}$ , lungo l’asse y, a 3.0 m/sec. Con quale velocità vede muovere la goccia il signore Antonio posto sul ciglio della strada vicino ai binari?
a) 112 km/h
b) 4.2 m/sec
c) -3,45 m/sec
d) 8,7 m/sec
Suggerimento
Cominciamo a scegliere bene i due sistemi di riferimenti, quello fisso e quello mobile…
Risoluzione
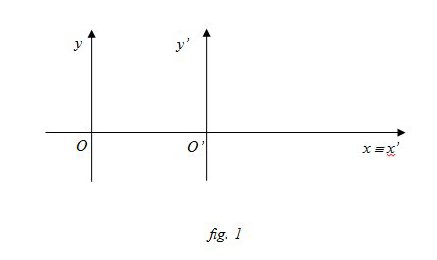
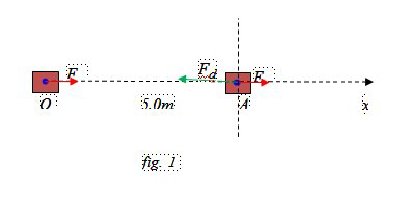
Scegliamo il riferimento fisso, centrato in O, osservatore sul ciglio della strada, con l’asse x parallelo alla direzione di moto del treno e l’asse y perpendicolare alla direzione del treno; mentre il riferimento mobile è centrato in O’, osservatore seduto sul treno vicino al finestrino, con l’asse x’ parallelo alla direzione del treno e l’ass y’ perpendicolare alla direzione del treno (fig. 1). Notiamo che in realtà gli assi x ed x’ e y ed y’ sono paralleli, ma possiamo ragionare sulla figura 1.
 Rappresentiamo le velocità indicate dal testo dell’esercizio nel riferimento O’x’y’ (fig. 2):
Rappresentiamo le velocità indicate dal testo dell’esercizio nel riferimento O’x’y’ (fig. 2):
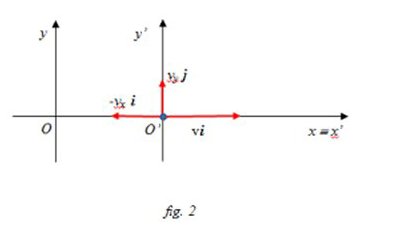
per la goccia:
\[v_{x}=-16m/sec\, \, \, \, \, \, \, v_{x}\vec{i}=(-16m/sec)\vec{i}\]
\[v_{y}=3,0m/sec\, \, \, \, \, \, \, v_{y}\vec{j}=(3,0m/sec)\vec{j}\]
per il treno:
\[\vec{v}=v\vec{i}=(68\, km/h)\vec{i}=\left ( 18,9\, m/sec \right )\vec{i}\]
ove i e j sono i versori degli assi. Evidentemente l’osservatore O, posto sul ciglio della strada, vede il treno muoversi con velocità v = ( 18.9 m/sec ), velocità di trascinamento.
Di conseguenza vedrà la goccia muoversi con velocità lungo l’asse x:
\[v\vec{i}+v_{x}\vec{i}=\left ( 18,9\, m/sec \right )\vec{i}+\left ( -16\, m/sec \right )\vec{i}=(2,9m/sec)\vec{i}\]
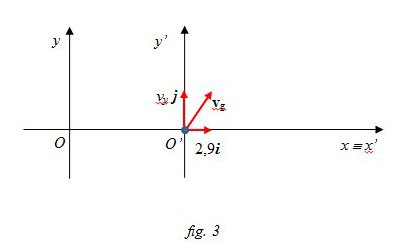
Il modulo della velocità della goccia, vg , si calcola con il teorema di Pitagora e vale
\[v_{g}=\sqrt{\left ( 3.0 \right )^{2}+\left ( 2,9 \right )^{2}}=\sqrt{17,41}=4,17\]
cioè 4.2 m/s ovvero circa 15 km/h. Il vettore vg vale invece
\[\vec{v}_{g}=(2,9\, m/sec)\vec{i}+(3,0\, m/sec)\vec{j}\]
Esercizio 1.10.– Un ragazzo lancia una pietra da un’altezza di 1.9 m al di sopra della superficie di uno stagno in direzione orizzontale e parallela alla superficie dello stagno con velocità V = 4,2 /sec. Con quale velocità la pietra entra in acqua?
Suggerimento: Calcolare il tempo di caduta quindi la velocità della pietra perpendicolare alla superficie dello stagno al tempo t = tempo di caduta e poi la velocità con cui la pietra entra in acqua.
Risoluzione ragionata
Indicato con v la velocità della pietra quando entra in acqua si vede che il problema è risolto con il seguente ragionamento:
\[v=\sqrt{v_{x}^{2}+v_{y}^{2}}\]
\[v_{y}=g\cdot t_{caduta}\]
\[t_{caduta}=\sqrt{\frac{2s}{g}}\]
Per la risoluzione basta applicare le seguenti formule, sostituire i dati, in senso inverso, dall’ultima alla prima.
Esercizio 1.11.- Una pallina viene lanciata con velocità orizzontale di 5,3 m/sec, da quale altezza deve essere lanciato in modo che tocchi terra formando un angolo di 45° gradi con il suolo?
Esercizio 1.12.- Vettore posizione e velocità all’istante t, accelerazione all’istante t. Vedi esercizio svolto
Esercizio 1.13.- Lancio di un oggetto verso l’alto. Vedi esercizio svolto nel mio canale Youtube
Esercizio 1.14.- Due automobili A e B partono da ferme e percorrono una strada rettilinea lunga 376 km in direzioni contrarie Sapendo che la velocità delle due automobili è 100 km/h e 135 km/h stabilire dopo quanto tempo s’incontrano e quanto spazio hanno rispettivamente percorso.
Suggerimento (fig. 1)
Risoluzione
Scegliamo il riferimento come nella figura 1, ossia Ox con l’origine in O º A. Indichiamo con V = 100 km/h e V’ = 135 km/h le due velocità delle rispettive automobili. Indichiamo con x …
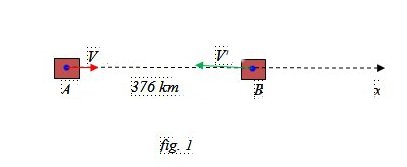
Indichiamo con x la spazio percorso dall’automobile A all’istante t dell’incontro con l’automobile B. L’automobile B all’istante avrà percorso lo spazio 376 – x.
In base alla relazione tra spazio e tempo nel caso di velocità costante si ha:
$\displaystyle s=vt$ ( per l’auto A)
$\displaystyle s’=v’t$ ( per l’auto B)
essendo in entrambi i casi lo spazio iniziale zero. Ricavando t da entrambe le relazioni si ottiene l’equazione:
S/V = S’/V’
ossia \[\frac{x}{100}=\frac{376-x}{135}\Rightarrow 135x=100\left ( 376-x \right )\Rightarrow 27x=20(376-x)\Rightarrow 47x=7520\Rightarrow x=160\, km\]
Le due automobili s’incontrano a 160 km di distanza dal punto A. Il tempo impiegato a percorrere il tratto di entrambe si può calcolare con la formula inversa di $\displaystyle s=vt$ e si ottiene:
t = S/v = 160/100 = 1,6 h
Esercizio 1.15.- Una palla viene lanciata da un’altezza di 50 m con velocità di 60 m/sec e con un angolo di 50° gradi. Calcolare la gittata. Calcolare inoltre la gittata nel caso in cui l’angolo di tiro sia di 0° gradi.
Esercizio 2.1.– Dinamica. Un’auto giocattolo ha una massa di 0,50 kg è spinta sulla sabbia per 40 cm con una forza di 1,2 N. Stabilire, senza considerare l’attrito, la velocità finale dell’auto
A) meno di 2,3 km/h
B) 5,0 km/h
C) 2,3 m/s.
Esercizio 2.2.– Esercizio sulle forze parallele e concordi. Vedi esercizio svolto
Esercizio 2.3.– Forze parallele e discordi. Vedi esercizio svolto
Esercizio 2.4.- Una cassa di 10 kg, inizialmente ferma, è tirata su un pavimento orizzontale per un tratto di 5,0 m da una forza orizzontale d’intensità 40 N. Se la velocità al termine dello spostamento è di 2,0 m/s, qual è il coefficiente di attrito?
Suggerimento
Scegliamo il riferimento come nella figura 1, ossia Ox con l’origine in O.
Esercizio 2.5.-Un’auto ferma su di un piano inclinato. Vedi esercizio svolto
Esercizio 2.6.- Due nuotatori Elio e Patrizia stanno in piscina nuotando in corsie differenti e parallele. Elio vede Patrizia nuotare verso di lui con velocità di 1,8m/s. Patrizia incrocia Elio e continua a nuotare alla stessa velocità fino a raggiungere il bordo della piscina, si gira e insegue Elio, il quale ad un certo punto vede Patrizia superarlo con velocità di 0,8 m/s. Tenendo conto che Elio nuota tutto il tempo con la stessa velocità, stabilire la velocità di nuoto dei due.
Esercizio 2.6.- Martina sta giocando in un prato e lancia una biglia su di una pista che ha disegnato sul prato. La biglia ha una massa di 10 grammi e dopo aver percorso 55 cm si ferma a causa della forza d’attrito pari a 7,8 x 10^ -2 N. Calcolare la velocità con cui Martina ha lanciato la biglia
A) meno di 3 km/h
B) 12,4 m/s
C) 10 m/s.
Esercizio 2.7.- Ad un corpo di massa 2,50 kg appoggiato su di un piano orizzontale è applicata una forza di trazione di 50,0 newton che forma un angolo di 45 gradi con l’orizzontale. Il coefficiente di attrito statitco tra il corpo e il piano è 0,250 e quello dinamico è 0,150.
Stabilire se il corpo si muove. Calcolare inoltre l’eventuale accelazione e il suo modulo.
Suggerimento
Rappresentare con un schizzo il relativo diagramma di corpo libero, in un riferimento con l’asse x parallelo al piano e l’asse y perpendicolare al piano. Le forze in gioco sono la forza di trazione $\displaystyle \overrightarrow{F}$, di modulo 50,0 N, la forza peso $\displaystyle F_{p}$ che agisce sul corpo, la forza di attrito statico $\displaystyle F_{s}$ e la forza di attrito dinamico $\displaystyle F_{d}$… e scomporre la forza di modulo F = 50,0 N in due compenti una llungo l’asse x e una lungo l’asse y tale che $\displaystyle \overrightarrow{F}=\overrightarrow{F_{x}}+\overrightarrow{F_{y}}$
Esercizio 2.8.- Per scendere lungo un tratto di lunghezza L di un piano inclinato privo di attrito, un blocco di plastica che parte da ferma impiega 1,5 secondi. Facendolo partire da un punto più alto in modo da percorrere 2,4 metri in più, impiega 0,5 secondi in più. Calcolare la lunghezza L del primo tratto.
Suggerimento
Scrivere due equazioni nelle incognite L ed a (accelerazione del corpo lungo il piano inclinato) tenendo conto che trattasi di un moto uniformemente accelerato. La prima equazione è $\displaystyle L=\frac{1}{2}a\cdot t^{2}$, mentre la seconda è $\displaystyle L+1,2=\frac{1}{2}a\cdot t^{2}$ , ove in entrambi i casi il tempo t è dato. Quindi…
Esercizio 2.9.- Un uomo di massa 80 kg si trova su di una bilancia pesapersone in una ascensore che scende verso il basso con una accelerazione di 0,38 metri al secondo quadro. Determinare la massa dell’uomo indicata dalla bilancia.
Esercizio 2.10.- Se una massa cade per 1,00 metri in 0,451 secondi, calcolare l’intensità locale dell’accelerazione di gravità e il periodo di un pendolo di lunghezza 0,500 metri in quel luogo.
Suggerimento. Il periodo del pendolo semplice è $\displaystyle P=2\pi \sqrt{\frac{L}{g}}$, ove g è l’accelerazione di gravità del luogo. Dunque bisogna prima calcolare l’accelerazione di gravità del luogo ove si trova il pendolo. Per il corpo che cade da un’altezza h possiamo calcolare l’accelerazione con cui cade sapendo il tempo che impiega a cadere utilizzando le formule del moto uniformemente accelerato: $\displaystyle h=\frac{1}{2}at^{2}\rightarrow a=\frac{2h}{t^{2}}$ …
Esercizio 2.11.- Un pendolo posizionato all’interno di un palazzo è utilizzato per un esperimento. Sappiamo che non è visibile il punto in alto al quale è ancorato il pendolo e che la massa appesa al pendolo è visibile e compie 13 oscillazioni in 110 secondi e che in quel luogo g = 9,81 m/s^2. Calcolare la lunghezza del pendolo.
Esercizio 2.12.- Al museo delle scienze di Valencia per un po’ di tempo oscillava nell’atrio del museo un pendolo di lunghezza 22,9 metri al quale era appesa una massa di 91 kg. Calcolare il periodo del pendolo e il tempo impiegato per oscillare dalla posizione di massimo spostamento fino alla posizione di equilibrio. Rifare l’esercizio immaginando che il pendolo sia nel palazzo delle Nazioni Unite di New York e a Parigi.
Suggerimento: Serve l’accelerazione di gravità di ogni luogo. Ricercarla su internet… o calcola qui
Esercizio 2.13.- Una piccola sfera di metallo è sospesa mediante un filo lungo L = 84 cm, a un chiodo indicato nella figura con A. Un secondo chiodo, indicato con B, si trova più in basso, sulla verticale del primo, ad L’ = 3L/4. La sfera viene spostata in modo tale che il filo teso formi con la verticale un angolo di 5° e poi lasciata andare. Oscillando, il filo tocca il secondo chiodo posto in B. Calcolare il tempo necessario affinché la sfera inverta il moto.
Suggerimento: Calcolare prima il periodo del pendolo di lunghezza L, e poi sommarci il periodo del pendolo di lunghezza L” = L/4, … Risultato t = 0,69 secondi.
Esercizio 2.14.- Il lavoro totale compiuto su u
Esercizio 3.1.- Lavoro ed Energia.- Una palla viene lanciata verso l’alto e raggiunge la sua altezza massima h, stabilire nella fase di caduta, in quale punto la sua energia potenziale è uguale alla sua energia cinetica.
Risposte:
A: h/8;
B: h/4;
C: h/2;
D) Non si può fare per insufficienza di dati.
Risoluzione
Dovendo essere in un certo punto A l’energia potenziale uguale all’energia cinetica deve valere la seguente uguaglianza \[mgh_{A}=\frac{1}{2}mv_{A}^{2}\] e semplificando la massa m della palla si ha
\[gh_{A}=\frac{1}{2}v_{A}^{2}\]
e ricavando \[h_{A}\] si ha:
\[*)\, \, \, \, \, \, \, h_{A}=\frac{1}{2g}v_{A}^{2}\]
ove \[h_{A}\] è l’altezza del punto A.
Applichiamo ora il principio di conservazione dell’energia meccanica tra il punto B, di altezza h (massima altezza della palla) e il punto A e si ha:
\[E_{c}\left ( A \right )+mgh_{A}=E_{c}\left ( B \right )+mgh_{B}\]
e tenendo conto che \[E_{c}\left ( B \right )=0,\, \, E_{c}\left ( A \right )=\frac{1}{2}mv_{A}^{2}\]
si ha:
\[\frac{1}{2}mv_{A}^{2}+mgh_{A}=0+mgh_{B}\]
ossia
\[\frac{1}{2}mv_{A}^{2}+mgh_{A}=mgh_{B}\]
\[\frac{1}{2}v_{A}^{2}+gh_{A}=gh_{B}\]
\[**)\, \, \, \, \, \, \, \frac{1}{2}v_{A}^{2}=gh-gh_{A}\]
essendo\[h=h_{B}\]
Sostituendo la (**) in (*) si ha:
\[h_{A}=\frac{gh-gh_{A}}{g}\]
\[h_{A}=h-h_{A}\, \, \Rightarrow \, \, 2h_{A}=h\, \, \Rightarrow\, \, h_{A}=\frac{h}{2}\]
Esercizio 3.2.- Un’automobile di massa 15 quintali parte da ferma e accelera per 5 secondi percorrendo 75 m. Calcolare la forza esercitata dal motore dell’automobile e il lavoro motore compiuto.
Esercizio 3.3.- Il lavoro totale L è compiuto su un’auto di massa m che viaggia in folle per x metri lungo un pendio inclinato rispetto all’orizontale di alfa gradi. Determinare l’intensità della forza dovuta alla resistenza dell’aria.
Risolvere il problema nel caso particolare: $L=4,75\cdot 10^{4}J$, x = 35 m, $\alpha =8^{\circ}$
Risoluzione ragionata
Lungo il piano inclinato, senza considerare gli attriti, la forza che fa spostare l’auto in folle è la componente parallalela della forza peso. A tale forza di oppone la forza dovuta alla resistenza dell’aria. Perntanto la forta totale agente sull’auto è \[F_{Tot}=P_{//}-F_{aria}\]
Dunque calcoliamo la componente P parallela della forza peso e la forza totale agente consocendo il lavoro L svolto per spostare l’auto di x metri e dalla formula precendente ricaviamo la forza dovuta alla resistenza dell’aria
Esercizio 3.4.- Un oggetto di massa m viene trascinato per x metri lungo una salita inclinata di 30° gradi rispetto all’orizzontale da una forza F parallela al piano inclinato. Trascuarando l’attrito qual è il lavoro compiuto dalla risultante di tutte le forze che agiscono sull’oggetto.
Risolvere nel caso particolare F = 100 N e x = 2 metri
Esercizio 3.5.- Ripetere l’esercizio 3.4 immaginando di stare sulla Luna.
Esercizio 3.5.1- Calcolare il lavoro fatto da una forza costante di 300 N, sapendo che la sua retta d’azione forma con la direzione dello spostamento un angolo di 60° e che lo spostamento è 50m. [Risultato: 12500 J ]
Esercizio 3.5.2- La massa di un ciclista è 70 kg e quella della sua bicicletta è 8 kg. Qual è il lavoro fatto dal ciclista per superare un dislivello di 500 m percorrendo una strada di montagna lunga 6 km, trascurando l’attrito. [Risultato: 3822000 J ]
Esercizio 3.5.3- Quale energia potenziale associata alla forza peso acquista un corpo di massa m = 10 kg inizialmente fermo, se viene spinto verticalmente verso l’alto da una forza di 300 N per 5 secondi? [Risultato: 247450 J ]
Esercizio 3.5.4- Un corpo di massa 5 kg possiede una energia potenziale di 9800 J. Con quale velocità giunge al suolo se cade liberamente? [Risultato: 62,6 m/s ]
Esercizio 3.5.5- Quale energia cinetica acquista un corpo libero inizialmente fermo di massa m = 12 kg se sottoposto per 10 secondi all’azione di una forza di 30 N sempre nella stessa direzione e nello stesso verso? [Risultato: 3750 J ]
Esercizio 3.5.6- Qual è la massa di un corpo libero inizialmente fermo che sottoposto all’azione di forza costante di 50 N acquista in 12 secondi l’energia cinetica di 1000 J? [Risultato: 180 kg ]
Esercizio 3.6.- Teorema dell’energia cinetica applicato al piano inclinato
Vedi video di un esercizio svolto sul mio canale Youtube
Esercizio 4.1.- Lavoro di una forza elastica.- Calcolare il lavoro necessario per allungare di 4 cm la molla della figura senza accelerarla. Si sa che se si appende alla molla un corpo avente massa 4 kg la molla si allunga di 2 cm.
Esercizio 5.1.- Un razzo di massa m esaurita la scorta di carburante si trova con velocità V = 0 ad una altezza di 125 x 10 km al di sopra della superficie terrestre. Sotto l’azione della forza gravitazionale terrestre cade verso la Terra. Calcolare la velocità con la quale il razzo incontra l’atmosfera terrestre, supponendo che questa inizi ad una altezza h = 130 km.
Esercizio 5.2.- Consideriamo tre corpi di massa m = 60 g situati nei vertici di un triangolo equilatero di lato l = 20 cm. Determinare il centro di massa del sistema dei tre corpi.
Esercizio 5.3.- Un astronauta vuole misurare la massa inerziale del suo orologio e utilizza il carrello delle masse. Il periodo di oscillazione del carrello con l’orologio è di 0,58 sec, mentre il periodo di oscillazione del carrello con il kilogrammo è di 1,45 sec. Qual è la massa dell’orologio?
Risoluzione
(Ricordiamo che la grandezza che determina l’inerzia di un corpo si chiama masa inerziale e che si definisce utilizzando il carrello delle masse, costituito da da un carrello, provvisto di indice, collegato ad una molla, a sua volta fissata ad una parete. Quindi per misurare la massa inerziale di un oggetto si mette sul carrello delle masse). Il periodo di oscillazione del carrello con l’orologio è dato dalla seguente formula \[T_{0}=2\pi \sqrt{\frac{m}{k}}\]
In tale formula non si si conosce il valore della costante elastica k. Ma si può calcolare ricavandola sapendo il periodo di oscillazione del carrello con il kilogrammo applicando la seguente formula \[T_{0}=2\pi \sqrt{\frac{m}{k}},\, \, \, \, \, T_{c}=2\pi \sqrt{\frac{1 kg}{k}}\]
Qui preferiamo invece ricavare direttamente una formula che esprime la massa m dell’orologio dell’astronauta. Dalle formule:
,
ricaviamo la radice quadrata di k in entrambe le formule, con To e Tc i periodi di oscillazione dell’orologio sul carrello e del kg sul carrello, e si ottiene: \[\sqrt{k}=\frac{2\pi\sqrt{m} }{T_{0}},\, \, \sqrt{k}=\frac{2\pi\sqrt{1\, kg} }{T_{c}}\]
e uguagliamo i secondi membri, si ha \[\frac{2\pi\sqrt{m} }{T_{0}}=\frac{2\pi\sqrt{1\, kg} }{T_{c}}\] avendo indicato con m la massa dell’orologio. Quindi semplificando e ricavando m si ha \[\sqrt{m}=\frac{T_{0}}{T_{c}}\sqrt{1kg}\Rightarrow m=\left ( \frac{T_{0}}{T_{c}} \right )^{2}\cdot 1\, kg\]
Con quest’ultima formula calcoliamo il valore della massa dell’orologio (m), sostituendo i dati nella formula stessa \[m=\left ( \frac{0,58\, sec}{1,45\, sec} \right )^{2}\cdot 1\, kg=0,16\, kg\]
Vedi il video esercizio svolto
Esercizio 5.4.- Ancora Lavoro ed Energia Un’ automobile avente massa di 1200 kg si muove su una strada inclinata di 5° con velocità V = 36km/h. Calcolare il lavoro che il motore compie in 5 minuti e la potenza da esso sviluppata Trascurare tutti gli effetti dovuti all’attrito.
Esercizio 5.6.- Un blocco scivola senza attrito su un piano orizzontale con velocità costante di 0,7 m/sec. Ad un certo punto il piano orizzontale si inclina di 18° gradi e il blocco scivola lungo un piano inclinato con coefficiente d’attrito dinamico \[\mu _{d}=0,11\] e raggiunge la fine del piano inclinato in un tempo pari a 1,6 secondi. Determinare la lunghezza del piano inclinato.
Suggerimento: \[a=\frac{F}{m}=\frac{P_{\parallel }-F_{A_{d}}}{m}=\frac{mgsen\alpha -\mu _{d}mgcos\alpha }{m}=…\]
Quindi calcolare la lunghezza del piano inclinato con la formula \[s=s_{0}+v_{0}t+\frac{1}{2}at^{2}\]
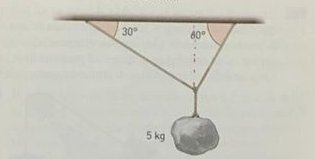
Esercizio 5.7.- Un corpo di massa 5 kg è appeso a due funi indicato in figura, determinare le tensioni \[T_{1},\, \, T_{2}\] nelle funi.
 Problema assegnato alle Olimpiadi di Fisica, gara di secondo livello. Anno 2001
Problema assegnato alle Olimpiadi di Fisica, gara di secondo livello. Anno 2001
Suggerimento: applicare il secondo principio della dinamica al corpo di massa 5kg, le forze in gioco sono la forza peso P e la tensione T nel filo (indicato nella figura). Evidentemente la tensione T nel filo è l’opposto della forza peso P. Quindi, nota la tensione T si calcolano le tensioni \[T_{1},\, \, T_{2}\] nelle funi con i teoremi sui triangoli rettangoli.
Esercizio 5.8.- Due pacchi di massa M1=4,6 e m2= 2,4 kg sono sospesi ai due estremi di una corda che passa per una carrucola (macchina di Atwood). Trascurando la massa della corda e pensando che la carrucola sia ideale calcolare con quale accelerazione si muovono i due pacchi e quanto vale la tensione della corda.
Risultati: 3,1 m/sec^2 verso l’alto per il pacco di massa minore, verso il basso per quello di massa maggiore; 31 N
Esercizio 5.9.- Una forza F = (6t)i, F in newton, agisce su di una particella di massa 2 kg, trovare il lavoro compiuto dalla forza nei primi due secondi supponendo che la particella parta da ferma.
Esercizio 5.10.- Una moto passa davanti ad un distributore a 90 km/h, dopo 2 minuti passa un’automobile a 120km/h. Dopo quanto tempo s’incontrano? A che distanza dal distributore si incontrano?
Esercizio 5.11.-Una palla lanciata da terra con traiettoria parabolica ha una velocità vettoriale V=7,6i+6.1j all’altezza di 9.1 m dal suolo. Qual è l’altezza massima raggiunta dalla palla? Qual è la gittata?
Esercizio 5.12.- Un corpo A cade da una altezza h e allo stesso istante un altro B viene lanciato verso l’alto con velocità V. Con che velocità deve essere lanciato B per scontrarsi con A a metà altezza ?
Esercizio 5.13.- Un facchino tiene ferma una cassa di 33,5 kg appoggiata su una passerella inclinata alta 2,40 m e lunga 10,0 m. Qual è il valore della forza equilibrante necessaria a tenere la cassa in equilibrio (g = 9,80 N/kg).
Esercizio 5.14.- Un blocco scivola a velocità costante lungo un piano inclinato di 42° rispetto all’orizzontale. Stabilire il coefficiente di attrito dinamico tra i blocco e il piano inclinato.
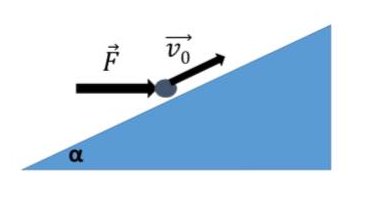
Esercizio 5.15.- Un punto materiale di massa m =12 Kg è posto su un piano inclinato (vedi figura) di un angolo α = 30 gradi con una velocità iniziale di modulo v0 = 3,0 m/s e diretta come in figura. Sul punto è applicata una forza orizzontale di modulo F = 100 N e diretta come in figura. Sapendo che il coefficiente di attrito dinamico tra punto e il piano inclinato è μd = 0.35, determinare 1) il modulo dell’accelerazione a del punto quando scivola verso l’alto; 2) la distanza d percorsa lungo il piano inclinato.
Risoluzione
Cominciamo a scegliere il riferimento, l’origine nel punto materiale l’asse x parallelo alla pendenza del piano inclinato e orientato verso l’alto, l’asse y perpendicolare all’asse x e orientato uscente dal piano inclinato. Applichiamo dunque il principio fondamentale della dinamica lungo l’asse x e lungo l’asse y. Lungo l’asse y non avviene il movimento e dunque la somma di tutte le forze agenti lungo l’asse y è zero. Il movimento avviene lungo l’asse x e dunque indicato con a l’accelerazione e con m la massa del punto materiale si ha:
\[m\cdot a=-P_{\left | \right |}-F_{d}+F_{\left | \right |}\]
con
\[P_{\left | \right |}=mgsen\alpha\]
\[F_{d}=\mu _{d}\left ( mg\cdot cos\alpha +F\cdot cos\alpha \right )\]
\[F_{\left | \right |}=F\cdot cos\alpha\]
Di conseguenza si ha \[m\cdot a=-mgsen\alpha +Fcos\alpha -\mu _{d}\left ( mgcos\alpha +Fsen\alpha \right )\]
e ricavando l’accelerazione si ha:\[a=\frac{-mgsen\alpha +Fcos\alpha -\mu _{d}\left ( mgcos\alpha +Fsen\alpha \right )}{m}=-2,1m/sec^{2}\]
Infine si ha che la distanza d è \[d=\frac{v_{0}^{2}}{2\left | a \right |}=2,1m\]
Esercizio 6.1.- Esercizio svolto sulla quantità di moto. Vedi il mio video nel mio canale Youtube
Esercizio 6.2.- Un bambino di massa 30,0 kg fermo su un carrello di massa 4,00 kg spara con un fucile giocattolo una pallina di 100 grammi in direzione orizzontale. La velocità della pallina è di 5,00 m/s. Calcolare l’energia acquisita dal sistema carrello-bambino e dalla pallina dopo lo sparo. Risultati: $3,68\times 10^{-3}J$, 1,25J.
Seconda parte.- Il bambino sale su un secondo carrello e ripete lo sparo. L’energia acquisita dalla pallina dopo lo sparo è 320 volte quella acquisita dal sistema carrello bambino. Calcolare la massa del secondo carrello
Risoluzione ragionata seconda parte
Inidichiamo con $m_{s}=m_{b}+m_{c}$ la massa del sistema bambino e secondo carrello, cioè $m_{s}=30+m_{c}$ e notiamo che l’energia cinetica del sistema bambino-carrello è 320 volte quella della pallina: \[E_{c}\left ( pallina \right )=320E^{‘}_{c}\left ( sist. carrello-bambino \right )\rightarrow E^{‘}_{c}=\frac{E_{c}}{320}\]
Quindi dalla formula dell’energia cinetica applicata al sistema bambino-carrello di massa $m_{s}$ e velocità $V_{s}$ si ha:
\[ E_{c}^{‘}=\frac{1}{2}m_{s}V_{s}^{2}\rightarrow \frac{E_{c}}{320}=\frac{1}{2}m_{s}V_{s}^{2}\]
con $E_{c}=1,25J$ e tenuto conto del principio di conservazione della quantità di moto:
\[ V_{s}=\frac{0,5}{m_{s}}\]
si ha il seguente sistema:
$\frac{1,25J}{320}=\frac{1}{2}m_{s}V_{s}^{2}$ e $V_{s}=\frac{0,5}{m_{s}}$
da cui $m_{s}= 32 kg$ e $m_{c}=2,0 kg$
