Formule per il coseno e per il seno: \[\begin{matrix} cos\left ( \alpha +\beta \right ) &=cos\alpha\, cos\beta -sen\alpha sen\beta \\ cos\left ( \alpha -\beta \right ) &=cos\alpha\, cos\beta +sen\alpha sen\beta \\ sen\left ( \alpha +\beta \right ) &=sen\alpha\, cos\beta +sen\beta cos\alpha \\ sen\left ( \alpha -\beta \right ) &=sen\alpha\, cos\beta -sen\beta cos\alpha \end{matrix}\]
Formule di addizione e sottrazione per la tangente e la cotangente
\[tan\left ( \alpha +\beta \right )=\frac{tan\alpha +tan\beta }{1-tan\alpha tan\beta }\]\[tan\left ( \alpha-\beta \right )=\frac{tan\alpha-tan\beta }{1+tan\alpha tan\beta }\]\[cot\left ( \alpha+\beta \right )=\frac{cot\alpha\cdot cot\beta-1 }{cot\alpha+cot\beta }\]\[cot\left ( \alpha-\beta \right )=\frac{cot\alpha\cdot cot\beta+1 }{cot\beta -cot\alpha }\]
Formule di duplicazione
\[\begin{matrix} cos\left ( 2\alpha\right ) &=cos^{2}\alpha\ -sen^{2}\alpha \\ sen\left ( 2\alpha \right ) &=2\cdot sen\alpha\, cos\alpha \\ \end{matrix}\]\[tan2\alpha =\frac{2tan\alpha }{1-tan^{2}\alpha }\]
\[cot2\alpha =\frac{cot^{2}\alpha-1 }{2cot^{2}\alpha }\]
Formule di bisezione
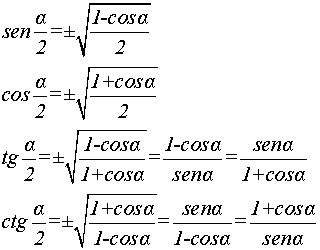
tg sta per tangente, ctg per cotangente.
Esempio 1.- Calcolare il seno di 15°. Applicando la formula di bisezione del seno si ha:\[sen15^{\circ}=sen\frac{30^{\circ}}{2}=\pm \sqrt{\frac{1-cos30^{\circ}}{2}}=\pm \sqrt{\frac{1-\frac{\sqrt{2}}{2}}{2}}=\frac{1}{4}\sqrt{2-\sqrt{3}}\] In pratica conoscendo il coseno di 30° si riesce a calcolare il seno di 15°. Giova ricordare che tra i segni ± va scelto il segno + in quanto il seno di 15° è situato nel primo quadrante, ove il seno è positivo. Questo esempio evidenzia come le suddette formule possono essere utilizzate per calcolare i valori delle funzioni trigonometriche non rientranti nella tabella dei valori fondamentali delle funzioni goniometriche.
Formule parametriche \[sen\,\alpha =\frac{2\, tan\frac{\alpha }{2}}{1+tan^{2}\, \frac{\alpha }{2}}\] \[cos\,\alpha =\frac{1- tan^{2}\frac{\alpha }{2}}{1+tan^{2}\, \frac{\alpha }{2}}\] Se si pone \[tan\frac{\alpha }{2}=t\] le suddette formule si trasformano nelle seguenti: \[sen\alpha =\frac{2t}{1+t^{2}}\] \[cos\alpha =\frac{1-t^{2}}{1+t^{2}}\] dette anche formule razionali.
Formule di prostaferesi
\[senp+senq=2sen\, \frac{p+q}{2}\cdot cos\, \frac{p-q}{2}\]
\[senp-senq=2cos\, \frac{p+q}{2}\cdot sen\, \frac{p-q}{2}\]
\[cosp+cosq=2cos\, \frac{p+q}{2}\cdot cos\, \frac{p-q}{2}\]
\[cosp-cosq=-2sen\, \frac{p+q}{2}\cdot sen\, \frac{p-q}{2}\]
\[tan\, p\pm tan\, q=\frac{sen\left ( p\pm q \right )}{cos\, p\cdot cos\, q}\]
\[cot\, p\pm cot\, q=\frac{sen\left ( q\pm p \right )}{sen\, p\cdot sen\, q}\]
Formule di Werner
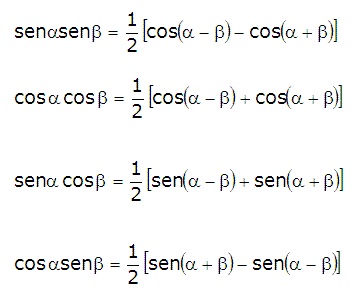
Le formule di Werner permettono di trasformare un prodotto in una somma e viceversa, in quest’ultima forma sono molto utili in tanti casi.
