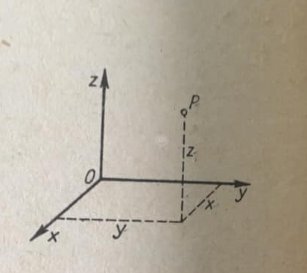
In un sistema di riferimento cartesiano dello spazio, indicato con Oxyz, ogni punto P dello spazio è identificato con una terna di numeri (x,y,z) dette le coordiante del punto P: x è l’ascissa, y, l’ordinata e z la quota \[P\left ( x,y,z \right )\]
Traslazione nello spazio
\[\left\{\begin{matrix} x= &x’+a \\ y= &y’+b \\ z= & z’+c \end{matrix}\right.\]
con O’ (a, b, c) nel riferimento Oxyz e P ( x’, y’, z’ ) nel riferimento traslato O’x’y’z’.
Traslazione inversa
\[\left\{\begin{matrix} x’= &x-a \\ y’= &y-b \\ z’= & z-c \end{matrix}\right.\]
Distanza tra due punti nello spazio
\[\overline{AB}=\sqrt{\left ( x_{2}-x_{1} \right )^{2}+\left ( y_{2}-y_{1} \right )^{2}+\left ( z_{2}-z_{1} \right )^{2}}\]
Punto medio di un segmento AB
\[x_{m}=\frac{x_{1}+x_{2}}{2},\, \, y_{m}=\frac{y_{1}+y_{2}}{2},\, \, z_{m}=\frac{z_{1}+z_{2}}{2}\]
Baricentro G di un triangolo
\[x_{G}=\frac{x_{1}+x_{2}+x_{3}}{3},\, \, y_{G}=\frac{y_{1}+y_{2}+y_{3}}{3},\, \, z_{G}=\frac{z_{1}+z_{2}+z_{3}}{3}\]
Equazione di un piano nello spazio
\[ax+by+cz+d=0\]
con a, b, c non contemporaneamente tutti nulli. L’equazione del piano si può scrivere anche nel seguente modo \[xcos\, \alpha +ycos\, \beta +zcos\, \gamma -\delta =0\] oppure \[x\rho cos\, \alpha +y\rho cos\, \beta +z\rho cos\, \gamma -\rho \delta =0\]
con \[a=\rho cos\alpha ,\, b=\rho cos\beta ,\, c=\rho cos\gamma ,\, d=-\rho \delta\]
\[\rho =\sqrt{a^{2}+b^{2}+c^{2}}\]
e \[cos\alpha ,\, cos\beta ,\, cos\gamma ,\, \] coseni direttori della retta n normale al piano e \[\delta =d(O,piano)\] è la minima distanza del piano dall’origine O.
Ricordiamo che il vettore n normale al piano ax +by +cz+d =0 ha componenti a, b, c: n(a, b,c)
Esempio 1.- La normale n ad un piano interseca il piano nel punto P(0,3,4), scrivere l’equazione del piano.
Le coordinate del punto P sono proporzionali a \[\delta =d(O,piano)\] e dunque \[\delta =\sqrt{0^{2}+3^{2}+4^{2}}=5\] \[cos\alpha =\frac{0}{5}=0,cos\beta =\frac{3}{5},cos\gamma =\frac{4}{5}\]. Pertanto si ha \[x\cdot 0+y\frac{3}{5}+z\frac{4}{5}-5=0\rightarrow 3y-z-25=0\]
Coseni direttori del piano ax+by+cz+d=0
\[cos\, \alpha =\frac{a}{\pm \sqrt{a^{2}+b^{2}+c^{2}}}\]
\[cos\, \beta =\frac{b}{\pm \sqrt{a^{2}+b^{2}+c^{2}}}\]
\[cos\, \gamma =\frac{c}{\pm \sqrt{a^{2}+b^{2}+c^{2}}}\]
Piani particolari nello spazio
- Piano passante per l’origine O del riferimento: \[d=0\rightarrow ax+by+cz=0\]
- Piano parallelo all’asse x: \[a=0\rightarrow by+cz+d=0\]
- Piano parallelo all’asse y: \[b=0\rightarrow ax+cz+d=0\]
- Piano parallelo all’asse z: \[c=0\rightarrow ax+by+d=0\]
- Piano parallelo al piano xy:\[a=b=0\rightarrow cz+d=0\]
Piano xy: z = 0 - Piano parallelo al piano xz: \[a=c=0\rightarrow by+d=0\]
Piano xz: y = 0 - Piano parallelo al piano yz: \[b=c=0\rightarrow ax+d=0\]
Piano yz: x = 0 - Piano che contiene l’asse x: \[a=d=0\rightarrow by+cz=0\]
- Piano che contiene l’asse y: \[b=d=0\rightarrow ax+cz=0\]
- Piano che contiene l’asse z: \[c=d=0\rightarrow ax+by=0\]
Equazione segmetaria del piano
\[\frac{x}{p}+\frac{y}{q}+\frac{z}{r}=1\]
Esempio 3.- Determinare l’equazione del piano passante per i punti A(-3,0,0), B(0,-1,0) e C(0,0,2).
Si ha \[\frac{x}{-3}+\frac{y}{-1}+\frac{z}{2}=1\rightarrow -2x-6y+3z=6\rightarrow 2x+6y-3z+6=0\]
Angolo tra due piani
\[cos\, \alpha =\left | \frac{aa’+bb’++cc’}{\sqrt{(a^{2}+b^{2}+c^{2})\cdot (a’^{2}+b’^{2}+c’^{2})}} \right |,\, \, \, \alpha \leq 90^{\circ}\]
Equazione di una retta
\[\left\{\begin{matrix} ax+by+cz+d &=0\\ a’x+b’y+c’z+d’ &=0 \end{matrix}\right.\]
una retta r è l’intersezione tra due piani di equazioni ax+by+cz+d=0 e a’x+b’y+c’z+d’ =0 e di conseguenza il vettore direzione v(l, m, n) della retta r ha componenti
l = ab’ – a’b, m =ac’ – a’c, n = bc’ – b’c.
Equazioni degli assi coordinati
\[\left\{\begin{matrix} y & =0\\ z & =0 \end{matrix}\right. \rightarrow asse\, x;\, \, \left\{\begin{matrix} x & =0\\ y & =0 \end{matrix}\right.\rightarrow asse\, z;\, \left\{\begin{matrix} x& =0\\ z& =0 \end{matrix}\right.\, \rightarrow asse\, y\]
Retta passante per due punti
\[\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\]
\[P_{1}(x_{1},y_{1},z_{1})\]\[P_{2}(x_{2},y_{2},z_{2})\]
$\displaystyle l=x_{2}-x_{1},\, \, m=y_{2}-y_{1},\: \: n=z_{2}-z_{1}$
Equazione parametrica della retta passante per il punto $\displaystyle P\left ( x_{0},y_{0},z_{0} \right )$ e di vettore direzione $\displaystyle \overrightarrow{v}\left ( l,m,n \right )$
\[\left\{\begin{matrix} x &=x_{0}+lt \\ y &=y_{0}+mt \\ z &z_{0} +nt \end{matrix}\right.\]
Esempio 4 .- Determinare l’equazione della retta passante per i due punti \[A\left ( -1,1,2 \right ),\, B(0,2,3)\]
Si ha: \[\frac{x+1}{0+1}=\frac{y-1}{2-1}=\frac{z-2}{3-2}\rightarrow \frac{x+1}{1}=\frac{y-1}{1}=\frac{z-2}{1}\rightarrow x+1=y-1=z-2\rightarrow \left\{\begin{matrix} x+1 &=y-1 \\ x+1&=z-2 \end{matrix}\right.\rightarrow \left\{\begin{matrix} x-y+2 &=0 \\ x-z+3 & =0 \end{matrix}\right.\]
Distanza di un punto da un piano
\[d=\frac{\left | ax_{0}+by_{0}+cz_{0}+d \right |}{\sqrt{a^{2}+b^{2}+c^{2}}}\]
\[P_{0}(x_{0},y_{0},z_{0})\] \[ax+by+cz+d=0\]
Piano passante per un punto
\[a\left ( x-x_{0} \right )+b\left ( y-y_{0} \right )+c\left ( z-z_{0} \right )=0\]
\[P_{0}(x_{0},y_{0},z_{0})\]
Piano passante per tre punti
L’equazione del piano passante per tre punti si può ricavare dalla seguente equazione
\[\begin{vmatrix} x-x_{1} &y-y_{1} &z-z_{1} \\ x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ x_{3}-x_{1} &y_{3}-y_{1} &z_{2}-z_{1} \end{vmatrix}=0\]
Piani paralleli e perpendicolari
I piani \[\alpha )\, ax+by+cz+d=0,\, \, \alpha\, ‘)\, a’x+b’y+c’z+d’=0\]
sono paralleli se: \[a:a’=b:b’=c:c’\]
Mentre sono perpendicolari se: \[a\cdot a’+b\cdot b’+c\cdot c’=0\]
Esempio 5.- Determinare l’equazione della retta passante per il punto P(0, -1, 2) e perpendicolare al piano 3x+2y-z-1=0
Tenuto conto che a = 3, b = 2, c = -1, si ha:
\[\frac{x-0}{3}=\frac{y+1}{2}=\frac{z-2}{-1}\rightarrow \frac{x-0}{3}=\frac{y+1}{2}=2-z\rightarrow \left\{\begin{matrix} \frac{x}{3} &=\frac{y+1}{2} \\ \frac{x}{3} & =2-z \end{matrix}\right.\rightarrow \left\{\begin{matrix} 2x-3y-3 &=0 \\ x+3z-6 & =0 \end{matrix}\right.\]
Ricordiamo che l’equazione della retta passante per il punto \[P\left ( x_{0},y_{0},z_{0} \right )\] e perpendicolare al piano di equazione ax+by+cz+d=0 ha equazione \[\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}=\frac{z-z_{0}}{c}\]
Intersezione tra due piani.- Si mettono a sistema le equazioni dei due piani.
Intersezione tra due rette.- Si mettono a sistema le equazioni delle due rette.
Condizione di complanarità tra due rette.- Due rette si dicono complanari se esiste un piano che lo contenga entrambe. Altrimenti si dicono sghembe.
Intersezione tra una retta ed un piano.- Si mettono a sistema l’equazione del piano con le equazioni della retta
Distanza di un punto da una retta.- Per determinare la distanza di un punto P da una retta r si calcola prima il piano $\alpha$ perpendicolare alla retta r e passante per il punto P, poi si interseca tale piano $\alpha$ con la retta r e si trova il punto H situato a minima distanza da P, quindi si calcola la distanza PH, che è la distanza di P da r. ( Il problema si può risolvere anche in altro modo, calcolando l’equazione della retta che passa P ed è perpendicolare ad r, si ottiene così il punto d’intersezione H e poi si applica la distanza tra i due punti P e H).
Minima distanza tra due rette r e t sghembe.- Si calcola prima l’equazione del piano contenente r e parallelo alla retta t. Poi si sceglie un punto P della retta t e si calcola distanza del punto P dalla retta r. (Tale distanza si può anche calcolare come la distanza tra due punti P e H delle rette r e t tali che il vettore PH si ortogonale alle rette r e t).
Esempio 6.- Data la retta r dello spazio d’equazione x = 1+z e y = 2z e il punto P(1,1,2), calcolare la distanza del P dalla retta r.
Risoluzione ragionata
Prima di tutto calcoliamo l’equazione del piano $\alpha$ perpendicolare ad r e passante per il punto P (1,1,2). Si dimostra che tale piano ha equazione x+2y+z-4=0.
Quindi troviamo il punto H di intersezione tra tale piano e la retta r, il che si ottiene mettendo a sistema l’equazione del piano e le equazioni della retta r. Si ottiene che il punto H ha coordinate H(3/2, 1, 1/2). Applicando infine la formula della distanza tra i due punti P e H si ottiene che la di stanza di P dalla retta r è: $PH=\frac{1}{2}\sqrt{10}$
Quindi troviamo il punto H di intersezione tra tale piano e la retta r, il che si ottiene mettendo a sistema l’equazione del piano e le equazioni della retta r. Si ottiene che il punto H ha coordinate H(3/2, 1, 1/2). Applicando infine la formula della distanza tra i due punti P e H si ottiene che la di stanza di P dalla retta r è: $PH=\frac{1}{2}\sqrt{10}$
AVVERTENZA.- Per ricordare gli elementi di teoria della geometria dello spazio si può vedere qui
Equazione della sfera
\[\left ( x-x_{0} \right )^{2}+\left ( y-y_{0} \right )^{2}+\left ( z-z_{0} \right )^{2}=r^{2}\]
r è il raggio e con centro \[C(x_{0},y_{0},z_{0})\]
Equazione dell’ellissoide di centro l’origine O del riferimento
\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1\]
Equazione dell’iperboloide ad una falda con semiassi reali a e b, c semiasse immaginario
\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1\]
Equazione dell’iperboloide a due falde con semiasse reale c, a e b semiassi immaginari
\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=-1\]
Paraboloide ellittico
\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=2z\]
Paraboloide iperbolico
\[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=2z\]
Cono
\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=0\]
Cilindro ellittico
\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\]
Cilindro iperbolico
\[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\]
\[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\]
Cilindro parabolico
\[y^{2}=2px\]
Coniche, curve di secondo grado. Clicca qui