Esempio 1.- Determinare la retta passante per il punto P (1,-2) e parallela alla retta r) y = – 2x+1.
Esercizio svolto sul mio canale Youtube
Determinare anche la retta passante per P (1,-2) e perpendicolare ad r.
Esempio 1.2.- Scrivi l’equazione della retta passante per il punto A(2, 1) che forma con la direzione positiva dell’asse x un angolo di 30° gradi. Clicca qui
Esempio 2.- Dato il triangolo rettangolo ABC, con A ( 6, 2 ), B( 3 ,-1 ), C( -2 , 4 ) , determinare un punto D in modo che ABCD sia un rettangolo.
Svolgimento sul mio canale Matematica Facile
Esempio 3.- Dato i tre punti A ( 2, 4 ), B( 6 , 2 ), C( 1 , 1 ) , determinare l’ortocentro del triangolo ABC.
Svolgimento sul mio Canale Youtube
Esempio 4.- Dato il triangolo ABC di vertice B( 6 , -1 ) determinare i vertici A e C del triangolo sapendo che la mediana CM del triangolo ha equazione y = -8x+16 e che l’altezza CD del triangolo ha equazione y = 4x+4. VEDI Qui
Esempio 5.- Trova i punti della retta 5x – 3y + 15 = 0 per i quali la distanza dall’asse x è 2/3 della distanza dall’asse y.
Risoluzione
Cominciamo a rappresentare la retta 5x-3y+15=0 nel piano cartesiano. Indichiamo con P (a,b) il generico punto della retta r e si ha: \[a=\frac{3b-15}{5}\]
ossia il punto P ha coordinate \[P\left (\frac{3b-15}{5},b \right )\]
Indichiamo con PH la distanza di P dall’asse x e si ha: \[\overline{PH}=\left | b-0 \right |=\left | b \right |\]
Indichiamo con PK la distanza di P dall’asse y e si ha: \[\overline{PK}=\left | \frac{3b-15}{5}-0 \right |=\left | \frac{3b-15}{5} \right |\]
Tenuto conto che \[\overline{PH}=\frac{2}{3}\cdot \overline{PK}\]
si ottiene l’equazione \[\left | b \right |=\frac{2}{3}\cdot\left | \frac{3b-15}{5} \right |\]
che risolta dà \[b=-\frac{10}{3},\, b=-\frac{10}{7}\]
Pertanto i punti richiesti sono due: \[P_{1}\left (-5, \frac{10}{3} \right ),\, \, P_{2}\left (-\frac{15}{7}, \frac{10}{7} \right )\]
Esempio 6.- Trovare le equazioni delle rette passanti per il punto P(0,-1) e che hanno distanza radical 5 dal punto A(3,3)
Risoluzione ragionata
Come prima cosa scrivi l’equazione del fascio di rette di centro il punto P. Quindi calcola la distanza tra il punto A e l’equazione del fascio di centro P. Uguaglia quindi tale distanza a radical 5 e risolvi l’equazione irrazionale con valore assoluto trovata nell’incognita m (coefficiente angolare del fascio di rette). Si vede che le rette richieste hanno equazioni rispettivamente
x – 2y – 2 = 0, 11x – 2y – 2 = 0
ottenute per m = 1/2 e m = 11/2.
Esempio 6.1- Dati il punto P(-2,0) e la retta r di equazione 3x – 4y + 12 = 0 determinare l’equazione della retta passante per l’origine O del riferimento e tale che il punto P sia equidistante da questa retta e da
Risoluzione
Disegniamo la retta r e indichiamo con PH la distanza di P da r: \[\overline{PH}=\frac{\left | 3(-2)-4(0)+12 \right |}{\sqrt{9+16}}=\frac{6}{5}\]
La retta passante per O(0,0) ha equazione y = mx ossia mx – y = 0.
La distanza di P(-2,0) dalla retta mx-y=0 è:\[d=\frac{\left | m(-2)-1(0)+02 \right |}{\sqrt{m^{2}+1}}=\frac{\left | -2m \right |}{\sqrt{m^{2}+1}}\]
Essendo d = PH si ottiene l’equazione \[\frac{\left | -2m \right |}{\sqrt{m^{2}+1}}=\frac{6}{5}\Rightarrow 16m^{2}-9=0\] da cui \[m=\pm \frac{3}{4}\] In definitiva le rette richieste sono: \[y=\pm \frac{3}{4}x\]
Esempio 7.- I punti A, B, C e D sono vertici di un quadrilatero convesso avente area 40. Sapendo che le coordinate dei vertici A, B e C sono rispettivamente (4, -4), (-2, 0) e ((0,6) e che il vertice D si trova sulla perpendicolare alla diagonale AC nel punto C determinare le coordinate del vertice D.
Risultato: D(90/29, 210/29)
Risoluzione
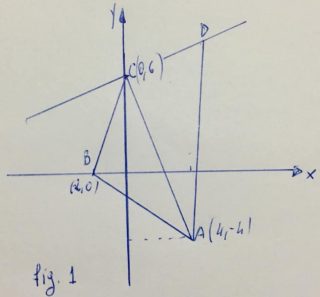
Indichiamo con h e k le coordinate del punto D (fig. 1) e calcoliamo il coefficiente angolare della diagonale AC, si ha \[m_{AC}=-\frac{5}{2}\]
Quindi la retta CD perpendicolare in C alla diagonale AC ha equazione: \[y=\frac{2}{5}x+6\]
Calcoliamo l’area del triangolo ABC e si ha che la sua area A’ è 22, di conseguenza l’area del triangolo ADC è 18 (18 = 40 – 22). Calcoliamo l’area del triangolo ADC in funzione di h e si ha che A” è uguale: \[A”(DCA)=\frac{1}{2}\begin{vmatrix} 4 & -4 & 1\\ 0 & 6 & 1\\ h & \frac{2}{5}h+6 & 1 \end{vmatrix}=\frac{1}{2}\left | -\frac{58}{5}h \right |\]
Pertanto richiedendo che l’area A” sia 18 si ricava l’equazione in h: \[18=\frac{1}{2}\left | -\frac{58}{5}h \right |\Rightarrow 18=\frac{1}{2}\left ( \frac{58}{5}h \right )\Rightarrow h=\frac{90}{29}\] e di conseguenza k = 210/29.
Esempio 8.- Tra le rette del fascio di centro P (4, 6) determinare quella che con gli assi cartesiani formano un triangolo di area 49.
Risultato: 2x+y-14=0, 9x+8y-84=0
Risoluzione
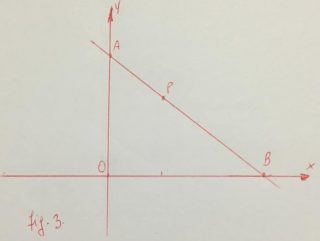
Calcoliamo l’equazione (fig. 3) del fascio di rette di centro P, si ha: y – 6 = m(x – 4) e di conseguenza le coordinate dei punti A e B rispettivamente d’intersezione del fascio con l’asse y e con l’asse x.
Si ha A(0, 6 – 4m) e B[(4m – 6)/m; 0].
Quindi sapendo che l’area del triangolo AOB è 49 si deduce l’equazione:\[49=\frac{\left | 6-4m \right |\cdot \left | \frac{4m-6}{m} \right |}{2}\Rightarrow \frac{\left ( 6-4m \right )^{2}}{m}=98\Rightarrow 8m^{2}+25m+18=0\] da cui m = -2, m = – 9/8.
Sostituendo tali valori nell’equazione del fascio si hanno le due rette richieste:
2x + y – 14 = 0, 9x + 8y – 84 = 0
Esempio 9.- Determinare le coodinate del vertice C di un triangolo ABC sapendo che è isoscele sulla base AB, che il vertice C si trova nel secondo quadrante, che le coordinate di A e B sono rispettivamente (-6,0) e (2, 6) e che la sua area è 25.
Risultato: C(-5,7)
Risoluzione
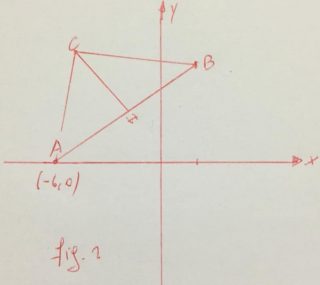
Indichiamo con h e k e le coordinate del punto C e calcoliamo (fig.2) l’equazione della retta AB, si ha
3x-4y+18 = 0.
Calcoliamo la distanza CH di C dalla retta AB, si ha: \[\overline{CH}=\frac{\left | 3h-4k+18 \right |}{5}\] e la distanza AB = 10
Sapendo che l’area del triangolo ABC è 25 possiamo ricavare, con la formula dell’area di un triangolo, l’equazione: \[25=\frac{10\cdot \frac{\left | 3h-4k+18 \right |}{5}}{2}\Rightarrow 25=\left | 3h-4k+18 \right |\]
E sapendo che il triangolo ABC deve essere isoscele, AC = BC, si ha prima \[\overline{AC}=\sqrt{\left ( h+6 \right )^{2}+k^{2}},\, \, \overline{BC}=\sqrt{\left ( h-2 \right )^{2}+\left ( k-6 \right )^{2}}\] e poi la relazione:
\[\sqrt{\left ( h+6 \right )^{2}+k^{2}}=\sqrt{\left ( h-2 \right )^{2}+\left ( k-6 \right )^{2}}\]
Pertanto mettendo a sistema si ottiene: \[\left\{\begin{matrix} \left | 3h-4k+18 \right | =&25 \\ \sqrt{\left ( h+6 \right )^{2}+k^{2}} & =\sqrt{\left ( h-2 \right )^{2}+\left ( k-6 \right )^{2}} \end{matrix}\right.\]
da cui h = 5 e k = 7
Esempio 10.- Detti T, S, R, Z rispettivamente i punti di intersezione tra la retta y = p e le rette t) y = 2x + 1, s) y = -x + 10, r) y= 1/2x – 1/2, z) y = -3/2x+19/2 determinare p in modo che i segmenti TS e RZ siano uguali.
Risoluzione ragionata
Mettiamo a sistema la retta y = p con ognuna delle rette t), s), r), z) e otteniamo rispettivamente le coordinate dei punti T, S, R, Z in funzione del parametro p. Si ha: P( (p -1) /2, p), S(10 – p, p), R(2p+1, p), Z( (19-2p)/3, p). Quindi calcoliamo le misure dei segmenti RS e RZ con la formula della distanza e uguagliamo le due espressioni in p ottenendo l’equazione in valore assoluto \[9\left | p-7 \right |=16\left | 2-p \right |\]
risolta la quale si ottiene $\displaystyle p=-\frac{31}{7}, p =\frac{19}{5}$
Altri esempi svolti di Geometria Analitica sul mio canale Youtube Matematica Facile
