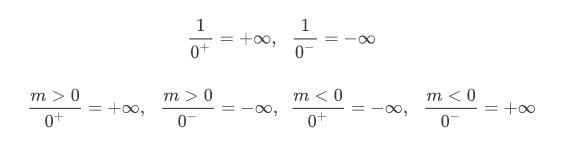Vogliamo calcolare alcuni limiti che danno luogo a forme convenzionali di immediata interpretazione (non sono dunque forme indeterminate).
Esempio 1.- Calcolare il limite \[\lim_{x\rightarrow +\infty }\frac{e^{-\left |2x^{2}+1 \right |}}{\sqrt{ln\left ( x-1 \right )}}\]
Esempio 2.- Calcolare il limite \[\lim_{x\rightarrow 1 }\frac{3^{\left | x-1 \right |}+\left ( \frac{1}{2} \right )^{\left | x+2 \right |}}{4^{\frac{1}{x-1}}}\]
Bisogna calcolare il limite destro e sinistro. Si ha:
\[\lim_{x\rightarrow 1^{+}}\frac{3^{\left | x-1 \right |}+\left ( \frac{1}{2} \right )^{\left | x+2 \right |}}{4^{\frac{1}{x-1}}}=\frac{3^{\left | 1-1 \right |}+\left ( \frac{1}{2} \right )^{\left | 1+2 \right |}}{4^{\frac{1}{1-1}}}=\frac{3^{0}+\left ( \frac{1}{2} \right )^{3}}{4^{\frac{1}{0^{^{+}}}}}=\frac{1+\frac{1}{8}}{4^{+\infty }}=\frac{9/8}{+\infty }=0\]
\[\lim_{x\rightarrow 1^{-}}\frac{3^{\left | x-1 \right |}+\left ( \frac{1}{2} \right )^{\left | x+2 \right |}}{4^{\frac{1}{x-1}}}=\frac{3^{\left | 1-1 \right |}+\left ( \frac{1}{2} \right )^{\left | 1+2 \right |}}{4^{\frac{1}{1-1}}}=\frac{3^{0}+\left ( \frac{1}{2} \right )^{3}}{4^{\frac{1}{0^{^{-}}}}}=\frac{1+\frac{1}{8}}{4^{-\infty }}=\frac{9/8}{0^{+} }=+\infty\]
Pertanto il limite assegnato non esiste.
Possiamo dunque affermare che valgono le seguenti forme convenzionali:
\[\frac{1}{0^{+}}=+\infty ,\, \, \, \, \frac{1}{0^{-}}=-\infty\]
\[\frac{m>0}{0^{+}}=+\infty ,\, \, \, \, \frac{m>0}{0^{-}}=-\infty,\, \, \, \frac{m<0}{0^{+}}=-\infty ,\, \, \, \, \frac{m<0}{0^{-}}=+\infty\]
\[\left\{\begin{matrix} a^{-\infty } &=0^{+} \, \, se\, \, a>0 \\ a^{-\infty } &=+\infty \, \, \, \, \, \, \, se\, \, 0<a<1 \end{matrix}\right.\]
\[\left\{\begin{matrix} a^{+\infty } &=+\infty \, \, se\, \, a>0 \\ a^{+\infty } &=0^{+} \, \, \, \, \, \, \, se\, \, 0<a<1 \end{matrix}\right.\]
Per ricordare tutte le forme convenzionali di immediata interpretazione clicca qui.
Esempio 3.- Calcolare il limite \[\lim_{x\rightarrow 2}(2x-4)^{\frac{1}{(x-2)^{2}}}\]
Osservato che \[(2x-4)^{\frac{1}{(x-2)^{2}}}=e^{(\frac{1}{\left ( x-2 \right )^{2}})\cdot ln(2x-4)}\]
si ha:
\[\lim_{x\rightarrow 2}(2x-4)^{\frac{1}{(x-2)^{2}}}=\lim_{x\rightarrow 2^{+}}e^{(\frac{1}{\left ( x-2 \right )^{2}})\cdot ln(2x-4)}=e^{+\infty \cdot (-\infty) }=e^{-\infty }=0\]
In generale possiamo dire che:
\[f(x)^{g(x)}=e^{g(x)\cdot lnf(x)}\rightarrow \left\{\begin{matrix} 0 & se\,\, g(x)\rightarrow -\infty \\ +\infty & se\, \, g(x)\rightarrow +\infty \end{matrix}\right.\]
con \[f(x)\rightarrow 0^{+}\]
ossia valgono le seguenti forme convenzionali:\[\left ( 0^{+} \right )^{+\infty }=+\infty \, \, \, ,\, \, \, \left ( 0^{+} \right )^{-\infty }=0\]
Esempio 4.- Calcolare il limite \[ \displaystyle \lim_{ x\to 2}arctan\left ( \frac{2+x}{4-x^{2}} \right )\]
.