Sia y = f(x) una funzione definita e continua nell’intervallo chiuso [a, b], derivabile nell’intervallo aperto (a, b) e tale che f(a) = f(b), allora esiste almeno un punto c dell’intervallo aperto (a, b) tale che: \[f'(c)=0\]
Dimostrazione
Poiché la funzione y = f(x) è continua nell’intervallo [a, b] per il teorema di Weierstrass* essa è dotata di massimo (M) e di minimo assoluto(m) in [a, b]. Indichiamo con \[x_{1},\, \, x_{2}\]
i due punti di [a,b] tali che\[f(x_{1})=m,\, \, f(x_{2})=M\](con m ≤ M).
Per continuare la dimostrazione distinguiamo due casi:
PRIMO CASO.-
Se M = m (cioè il massimo e il minimo assoluto coincidono) allora la funzione è costante nell’intervallo (a, b) e il teorema è dimostrato ricordando il fatto che la derivata di una funzione costante è sempre zero.
SECONDO CASO.-
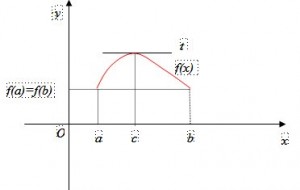
Interpretazione geometrica
Dal punto di vista geometrico (vedi figura) il teorema di Rolle afferma che per il grafico di una curva d’equazione y = f(x), continua in [a,b], con estremi di coordinate (a,f(a)) e (b,f(b)) di uguali ordinate, dotata di retta tangente in ogni punto di ascissa interna ad [a,b], esiste un punto P d’ascissa \[c\in \left ( a,b \right )\] in cui la tangente t alla curva è parallela all’asse x.
Esempio 1.. Vedi il seguente mio video

