\[\int \frac{x+1}{x^{3}-5x^{2}+8x-4}\, \, \, dx\]
Il polinomio al denominatore g(x) = x3 – 5x2 + 8x – 4 è di terzo grado, mentre quello dal numeratore f(x) = x + 1 è di primo grado. Pertanto, bisogna prima di tutto scomporre il denominatore utilizzando la regola di Ruffini, ovvero ricercare le soluzioni dell’equazione g(x) = x3 – 5x2 + 8x – 4 = 0. Quindi si ha la seguente identità:
\[x^{3}-5x^{2}+8x-4=\left ( x-1 \right )\left ( x^{2}-4x+4 \right )=\left ( x-1 \right )\left ( x-2 \right )^{2}\]
cioè la radice x = 2 è multipla, di molteplicità 2 (si ripete due volte) e la radice x = 1 è semplice. Allora è possibile determinare tre costanti reali A, B, C tali che:
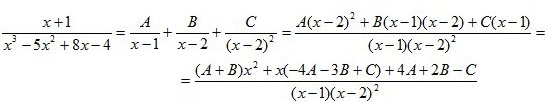
ove il numeratore dell’ultima frazione è ottenuto mediante i seguenti calcoli:
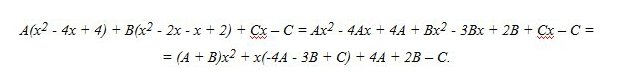
Quindi per il principio d’identità dei polinomi si deduce il seguente sistema:\[\left\{\begin{matrix} A+B &=0 \\ -4A+3B+C&=1 \\ 4A+2B-C&=1 \end{matrix}\right.\]e che risolto dà A = 2, B = -2, C = 3.
Pertanto l’integrale assegnato si calcola nel seguente modo:\[\int \frac{x+1}{x^{3}-5x^{2}+8x-4}\, \, \, dx=\int \frac{2}{x-1}\, \, dx+\int \frac{-2}{x-2}\, \, dx+\int \frac{3}{\left ( x-2 \right )^{2}}\, \, dx\] e vale:\[2ln\left | x-1 \right |-2ln\left | x-2 \right |+3\frac{\left ( x-2 \right )^{-1}}{-1}+c\]ossia:\[2ln\left | x-1 \right |-2ln\left | x-2 \right |-\frac{3}{x-2}+c\]
Nel mio canale Youtube puoi vedere altri integrali svolti.
