In preparazione
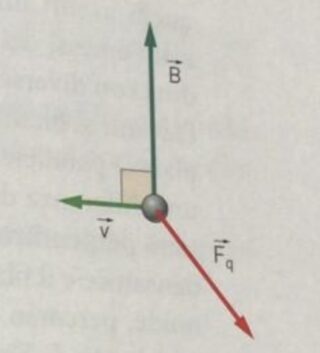
Esempio 1.- Una spira rettangolare è immersa in un campo magnetico uniforme di modulo $\displaystyle p\times 10^{-3}\, \, T$. Le linee del campo magnetico formano un angolo $\displaystyle \alpha$ con l’asse della spira che è attraversata da una corrente $\displaystyle i$. I lati della spira misurano rispettivamente $\displaystyle L_{1}$ e $\displaystyle L_{2}$. Sapendo che il momento della forza della spira vale $\displaystyle q\times 10^{-6}\, \, N$, calcolare il valore dell’angolo alfa.
Esempio 2.- Bisogna costruire un eletrodotto ad alta tensione da $\displaystyle p\times 10^{5}\, \, V$ che trasporta una potenza di q MW. A che altezza minima rispetto al suolo occorre stendere la linea perché al suolo non si ottenga un valore del campo magnetico superiore a quello terrestre (campo magnetico terrestre $\displaystyle 5,0\times 10^{-5}\, \, T$)?
Esempio 3.- Un elettrone entra in un campo magnetico uniforme di intensità p Tesla, con una velocità di v 10^6m/s che forma un angolo di 45° con le linee del campo magnetico. Calcolare il raggio della traiettoria elicoidale descritta dall’elettrone e il passo dell’elica.
Esempio 4.- La lancetta dei minuti di un orologio a muro è lunga q cm e quella delle ore p cm. Calcolare la velocità angolare, la frequenza e la velocità con cui si muovono le punte delle lancette.
Esempio 5.- La Stazione Spaziale ruota attorno alla Terra su un’orbita circolare impiega 93 minuti per fare un giro completo alla quota di 405 km dalla superficie terrestre. Se il suo moto è circolare uniforme calcolare la sua velocità e la sua accelerazione centripeta sapendo che il raggio terrestre è circa 6380 km.
Esempio 6.- Da quale altezza vinee lasciata cadere una biglia di vetro se la sua velocità di impatto al suolo è di 18,9 m/s. Quanto tempo impiega a cadere?
Esempio 7.-In quanto tempo una imbarcazione che naviga in linea retta alla velcità di 32 km/h raddoppia la sua velocità se può mantenere un’accelerazione costante di 1,8 m/s^2. Calcola lo spazio percorso durante la fase di accelazione.
Esempio 8.- In un circuito RLC circola una corrente efficace di p ampere e si ha una potenza media dissipata pari a q Watt. L’angolo di sfasamento è $\displaystyle 0<\alpha <90^{\circ}$. Calcolare il valore della tensione efficace. Risolvere poi il problema nel caso particolare $\displaystyle p=3,00\, A,\, q=310\, W,\, \, \alpha =30^{\circ}$
Risoluzione
Per risolvere l’esercizio possiamo ragionare nel seguente modo. Ricordiamo prima la formula per ottenere la tensione efficace
$\displaystyle f_{eff}=Z\cdot i_{eff}$
però non conosciamo Z e si può calcolare con la formula
$\displaystyle Z=\sqrt{R^{2}+\left ( \omega L-\frac{1}{\omega C} \right )^{2}}$
ove la resistenza R si può calcolare con la formula $\displaystyle R=\frac{P}{i_{eff}^{2}}$ e la quantità $\displaystyle \left ( \omega L-\frac{1}{\omega C} \right )$ con la formula: $\displaystyle \left ( \omega L-\frac{1}{\omega C} \right )=R\cdot tan\, \alpha$
Esempio 9.- La foglia oro è un foglio di questo metallo con spessori nominali standardizzati (spessore nominale = quantità in grammi di oro necessari per ottenere 1000 fogli quadrati di dimensioni stabilite e uguali fra loro). La foglia oro viene venduta in libretti, ciascuno dei quali contiene un un determinato numero di fogli identici. Calcolare lo spessore medio sm di un foglio di oro con spessore nominale 32 e lato di 80 millimetri (la densità dell’oro è 19320 kg/m^3. Calcolare il costo C relativo al materiale di un libretto da 25 fogli del tipo precedente (l’oro è quotato 36,25€/g
Risoluzione
Prima di tutto bisogna ben leggere il problema e capire cosa si intende per foglia d’oro. Poi per stabilire lo spessore medio s bisogna ricordare che la densità è il rapporto tra la massa e il volume e che il volume del foglio in questione si può ottenere come prodotto dell’area del foglio quadrato di lato 80 mm moltiplicato per lo spessore medio (da calcolare) del foglio. Quindi
V = As e d = m|V, da queste due formule si ricava che s = m/Ad
Teniamo pure conto che ogni foglio ha una massa d’oro pari a:
32g /1000 = 32 10^-3 grammi /foglio = 32 (10^-3)(10^3) kg/foglio
0,032 grammi = 8^2*ρ*sm
s = 0,032/(8^2*19,32) = 2,588*10^-5 cm = = 2,588*10^-7 m
costo
C = 36,25*32*25/1000 = 29,00 € / libretto da 25 fogli
