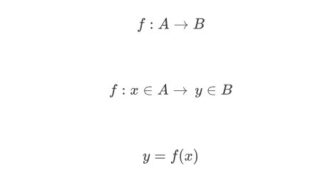Definizione di funzione.- Dati due insiemi A e B non vuoti si dice funzione o applicazione definita in A e a valori in B ogni regola o legge di corrispondenza che associ ad ogni elemento x di A uno ed un solo elemento y di B.
Per indicare una funzione si usa uno dei seguenti simboli:
\[f:A\rightarrow B\]
\[f:x\in A\rightarrow\, y\in B\]
\[y=f(x)\]
L’insieme A si dice dominio (o campo di esistenza, o insieme di definizione) della funzione, l’insieme B si dice insieme in cui la funzione assume valore. La x si dice variabile indipendente e la y variabile dipendente da x tramite la funzione f; la y si usa dire anche corrispondente di x o trasformato di x o anche immagine di x tramite f.
FUNZIONE INIETTIVA
Una funzione $\displaystyle f:A\rightarrow B$ si dice iniettiva se è verificata la seguente proprietà:
\[x_{1}\neq x_{2}\Rightarrow f(x_{1})\neq f(x_{2})\, \, \, \forall x_{1},x_{2}\in A\]
Un altro modo di provare che una funzione è iniettiva è utilizzare la seguente proprietà:
\[f(x_{1})=f(x_{2})\Rightarrow x_{1}=x_{2}\, \, \, \, \forall x_{1},x_{2}\in A\]
Vedi il mio video per capire meglio la definizione di funzione iniettiva
Esempio 1.- Stabilire se la seguente funzione è iniettiva \[f:x\in R\rightarrow x^{3}+3\in R\]
Vedi l’esempio svolto sul mio canale Youtube
Esempio 2.- Stabilire se la seguente funzione è iniettiva \[f:x\rightarrow x^{3}-2\]
Non sai fare l’esercizio? Allora vedi il mio video su Youtube
Esempio 3.- Stabilire se la seguente funzione reale di variabile reale è iniettiva \[y=x^{2}-4\]
Risposta: NO
FUNZIONE SURIETTIVA
Una funzione $\displaystyle f:A\rightarrow B$ si dice suriettiva se:
\[\forall y\in B\, \, \exists x\in A\, \, :y=f(x)\]
Vedi il mio video per capire meglio la definizione di funzione suriettiva
Esempio 1.- Stabilire se la seguente funzione è suriettiva \[f:x\in R\rightarrow x^{3}+4\in R\]
Vedi l’esempio svolto sul mio canale Youtube
Esempio 2.- Stabilire se la seguente funzione è suriettiva \[f:x\rightarrow x^{3}-2\]
Non sai fare l’esercizio? Allora vedi il mio video su Youtube
Esempio 3.- Stabilire se la seguente funzione reale di variabile reale è suriettiva \[y=x^{2}-4\]
Risposta: NO
FUNZIONE BIETTIVA
Una funzione $\displaystyle f:A\rightarrow B$ si dice biettiva o invertibile se è iniettiva e suriettiva.
In tal caso ha senso considerare la funzione inversa di f, denotata con $\displaystyle f^{-1}$, definita in B e a valore in A: \[f^{-1}:A\rightarrow B\]
Esempio 1.- Determinare la funzione inversa di \[f:x\in R\rightarrow x^{3}+1\in R\]
Vedi l’esempio svolto sul mio canale Youtube
Ulteriori esercizi
Esempio 1.-Date le funzioni:
\[f:x\rightarrow \frac{3}{x-5}, \, \, \, \, g:x\rightarrow x+3\]
determinare $\displaystyle f\, o\, g,\, g\, o\, f$ e risolvere la disequazione $\displaystyle (g\, o\, f)\left ( x \right )\geq g(f(-x))$
Esempio 2.-Data le funzione \[f(x)=\frac{2}{x-1}+1\] rispondere alle seguenti domande:
a) il dominio della funzione e l’insieme immagine;
b) dimostrare che la funzione f(x) è invertibile e determinare la funzine inversa, verificando che $\displaystyle f^{-1}=f$;
c) trovare f(2), f(-3/2) e le controimmagini di 3, 2, – 6;
d) calcolare f(f(x) e $\displaystyle \left ( fofof \right )\left ( x \right )$;
e) risolvere la disequazione \[(fof)\left ( x \right )+f(2x)>1\]