1) $\displaystyle dy=f'(x)\Delta x$
Mentre si dice differenziale della funzione y = f(x) nel punto d’ascissa $\displaystyle x=x_{0}$ il seguente prodotto:
$\displaystyle dy=f'(x_{0})\Delta x$
Esempio 1.- La funzione $\displaystyle y=x^{2}-4$ ha differenziale $\displaystyle dy=2x\Delta x$ mentre nel punto x = 2 ha differenziale $\displaystyle dy=2(2)\Delta x=4\Delta x$. La funzione $\displaystyle y=x^{3}-3x+1$ ha differenziale $\displaystyle dy=(3x^{2}-3)\Delta x$, mentre la funzione $\displaystyle y=e^{2x+6}$ ha differenziale $\displaystyle dy=2e^{2x+6}\Delta x$.
OSSERVAZIONE 1 – Nuovo aspetto del differenziale.
Considerata la funzione y = x, applicando ad essa la definizione di differenziale si ha: $\displaystyle dx=1\Delta x$ , da cui $\displaystyle \Delta x=dx$ , cioè il differenziale della variabile indipendente è uguale all’incremento della variabile. Pertanto l’espressione (1) può essere scritta nel seguente modo:
2) $\displaystyle dy=f'(x)dx$
Esempio 2.- Se $\displaystyle y=sen(3x)$ si ha che $\displaystyle dy=cos(3x)\cdot 3dx=3\cdot cos(3x)\cdot dx$.
Se invece la funzione è $\displaystyle y=ln(x^{2}+5x+7)$ il differenziale è
$\displaystyle dy=\frac{2x+5}{x^{2}+5x+7}dx$
Il differenziale di $\displaystyle y=ln(x^{2}+5x+7)$ per x = 2 è
$\displaystyle dy=\frac{2(2)+5}{(2)^{2}+5(2))+7}dx=\frac{9}{21}dx=\frac{3}{7}dx$
OSSERVAZIONE 2-. Derivata di una funzione secondo Leibnitz.
Dalla relazione d y = f ‘(x)dx si ricava $\displaystyle f'(x)=\frac{dy}{dx}$ oppure $\displaystyle y’=\frac{dy}{dx}$ , cioè la derivata di una funzione è uguale al rapporto tra il differenziale della funzione e quello della variabile indipendente.
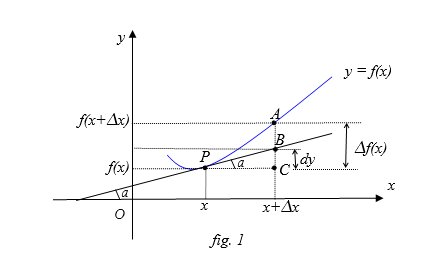
OSSERVAZIONE 3.- Significato geometrico del differenziale
Dal punto di vista geometrico il differenziale è uguale alla differenza tra l’ordinata del punto B ( fig. 1), d’ascissa $\displaystyle x+\Delta x$ , della retta tangente t alla curva d’equazione y = f(x) nel punto d’ascissa x e l’ordinata f(x) della curva, ossia:
3) d y = BC
Di conseguenza sostituire a $\displaystyle \Delta f(x)$ il differenziale $\displaystyle df(x)$ nell’intervallo $\displaystyle \left ( x,x+\Delta x \right )$ equivale geometricamente a sostituire la curva con la sua tangente.
Inoltre, dalla relazione:
4) $\displaystyle dy=\Delta f(x)-AB$
si evince che approssimando $\displaystyle \Delta f(x)$ con $\displaystyle df(x)$ si commette un errore dato da AB.
Tale approssimazione è tanto migliore quanto minore è AB, e quest’ultimo è tanto più piccolo quanto più piccolo è l’incremento $\displaystyle \Delta x$ .
Proprietà fondamentali dei differenziali.
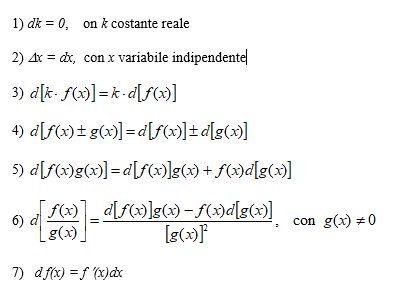
Applicazione del differenziale al calcolo approssimato.
Se l’incremento della variabile indipendente $\displaystyle \Delta x$ è piccolo in valore assoluto, allora il differenziale dy e l’incremento $\displaystyle \Delta y$ della funzione y = f(x), sono approssimativamente uguali, cioè
$\displaystyle \Delta y\approx dy$
ed esplicitando si ha:
$\displaystyle f(x+\Delta x)-f(x)\approx f'(x)\Delta x$
ossia:
$\displaystyle f(x+\Delta x)\approx f(x)+f'(x)\Delta x$
Esempio 1.- Calcolare l’incremento approssimato del lato di un quadrato se la sua area aumenta da $\displaystyle 9m^{2}$ a $\displaystyle 9,1m^{2}$ .
Risoluzione
Se x esprime l’area del quadrato e y è il suo lato, si ha $\displaystyle y=\sqrt{x}$. Essendo per ipotesi $\displaystyle x=9,\, \Delta x=0,1$, l’incremento del lato del quadrato è approssimativamente:
$\displaystyle \Delta y\approx dy=y’\Delta x=\left [ \frac{1}{2\sqrt{x}} \right ]_{x=9}\cdot \Delta x=\frac{1}{2\sqrt{9}}\cdot 0,1=\frac{1}{6}\frac{1}{10}=\frac{1}{60}m$
