Distribuzione normale o di Gauss

Una variabile casuale continua $\displaystyle X$ si dice normale o gaussiana, di parametri $\displaystyle \mu$ e $\displaystyle \sigma ^{2}$, se la distribuzione di probabilità è del tipo:

\[1)\, \, \, p(X)=\frac{1}{\sigma \sqrt{2\pi }}e^{-\frac{\left ( X-\mu \right )^{2}}{2}}\]

con $\displaystyle \mu =M(X),\, \, Var(X)=\sigma ^{2}$ .

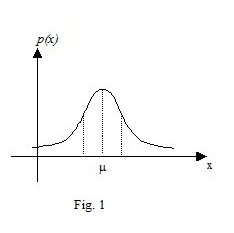
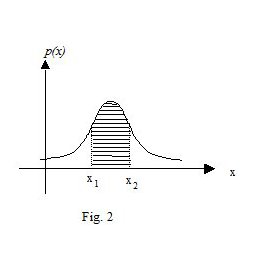
Nella figura 1 è rappresentata la gaussiana con la sua tipica forma a campana, mentre nella figura 2 è messo in evidenza che: \[Pr\left ( x_{1}\leqslant X<x_{2} \right )=\int_{x_{1}}^{x_{2}}p\left ( X \right )dX\]

Teorema.- Effettuando un insieme di prove tutte nelle stesse condizioni, la probabilità che la frequenza relativa di una dato evento E differisca, in valore assoluto, dalla probabilità a priori dell’evento stesso per meno di un numero e piccolo a piacere, tende ad 1 al crescere del numero delle prove.

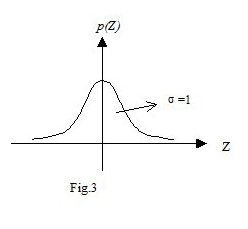
Nota.- Posto nella (1) $Z=\frac{X-\mu }{\sigma }$ si ottiene la gaussiana standardizzata di figura 3:

\[p(Z)=\frac{1}{\sqrt{2\pi }}e^{-\frac{Z^{2}}{2}}\]

con $\mu =0,\, \sigma^{2} =1$.

Trasformare una variabile gaussiana nella corrispondente standardizzata permette di calcolare qualsiasi probabilità utilizzando la tavola di probabilità della gaussiana standardizzata.
La seguente tavola rappresenta uno stralcio della tavola di probabilità della gaussiana
standardizzata e sarà utilizzata nei prossimi esercizi. A lato è riportala la tavola della funzione di ripartizione F(z) della variabile aleatoria gaussiana standardizzata.

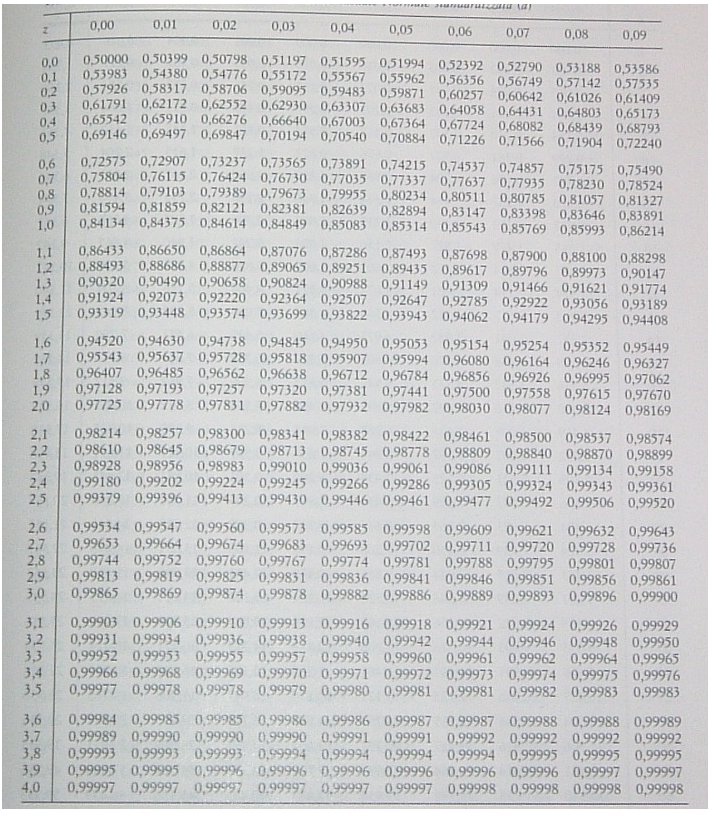
Tavola tratta da Statistica di Domenico Piccolo – Il Mulino – Bologna 2000