Definizione.- Si dice ellisse l’insieme dei punti del piano per i quali è costante la somma delle distanze da due punti fissi, detti fuochi.
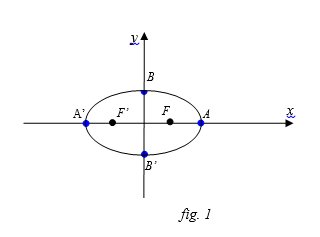
Equazione dell’ellisse canonica con i fuochi sull’asse x (fig. 1)
Equazione: \[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,\, \, \, \, con\, \, a >b\]
Vertici: \[A\left ( a,0 \right ),\, \, A’\left ( -a,0 \right ),\, \, B\left ( 0,b \right ),\, \, B’\left ( 0,-b \right )\]
Fuochi: \[F\left ( c,0 \right ),\, F’\left (-c,0 \right )\]
Asse maggiore e asse minore: \[\overline{AA’}=2a,\, \, \overline{BB’}=2b\]
Semiasse maggiore e seminasse minore: \[\overline{OA}=2,\, \, \overline{OB}=2\]
Distanza e semidistanza: focale:\[\overline{FF’}=2c,\, \, \overline{OF}=c\]
Uguaglianza fondamentale: \[c^{2}=a^{2}-b^{2}\]
Eccentricità: \[e=\frac{c}{a}<1\]
Disuguaglianza fondamentale: \[c<a\]
Esempio 1.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’ellisse d’equazione \[\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\]
Essendo \[a^{2}=16\Rightarrow a=\pm 4,\, \, b^{2}=9\Rightarrow b=\pm 3,\]
I vertici sono: \[A(4,0),\, A'(-4,0),\, B(0,3),\, B'(0,-3)\]
Dall’uguaglianza fondamentale dell’ellisse si ricava c: \[c^{2}=a^{2}-b^{2}\rightarrow c^{2}=16-9\rightarrow\, c^{2}=7\rightarrow c=\sqrt{7}\] e dunque i fuochi sono \[F(\sqrt{7},0), F'(-\sqrt{7},0)\]
L’eccentricità è: \[e=\frac{c}{a} =\frac{\sqrt{7}}{4}\]
Gli assi sono:…
Esempio 2.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’ellisse d’equazione \[3x^{2}+4y^{2}=1\]
Esempio 3.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’ellisse d’equazione\[12x^{2}+13y^{2}=156\]
Esempio 4.- Stabilire il valore del parametro reale k per il quale l’equazione \[ \frac{x^{2}}{2k+7}+\frac{y^{2}}{3+k}=1\] rappresenta una ellisse con i fuochi sull’asse x e avente per fuoco il punto $F\left ( \sqrt{7},0 \right )$
Equazione dell’ellisse canonica con i fuochi sull’asse y
Equazione:\[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,\, \, \, \, con\, \, a <b\]
Vertici: \[A\left ( a,0 \right ),\, \, A’\left ( -a,0 \right ),\, \, B\left ( 0,b \right ),\, \, B’\left ( 0,-b \right )\]
Fuochi: \[F\left ( 0,c \right ),\, F’\left (0,-c \right )\]
Asse minore e asse maggiore: \[\overline{AA’}=2a,\, \, \overline{BB’}=2b\]
Semiasse minore e seminasse maggiore: \[\overline{OA}=a,\, \, \overline{OB}=b\]
Distanza e semidistanza: focale:\[\overline{FF’}=2c,\, \, \overline{OF}=c\]
Uguaglianza fondamentale: \[c^{2}=b^{2}-a^{2}\]
Eccentricità: \[e=\frac{c}{b}<1\]
Disuguaglianza fondamentale: \[c<b\]
Esempio 1.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’ellisse d’equazione \[\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\]
Esempio 2.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’ellisse d’equazione \[5x^{2}+3y^{2}=1\]
Esempio 3.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’ellisse d’equazione \[3x^{2}+2y^{2}=6\]
Puoi consultare degli esercizi svolti sul mio canale Youtube.