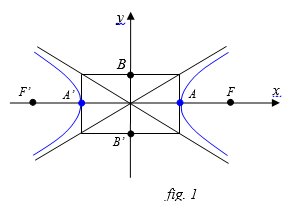
Equazione dell’iperbole canonica con i fuochi sull’asse x ( fig. 1 )
Equazione: \[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\]
centro di simmetria O(0,0)
Vertici: \[A\left ( a,0 \right ),\, \, A’\left ( -a,0 \right ),\, \, B\left ( 0,b \right ),\, \, B’\left ( 0,-b \right )\]
Fuochi: \[F\left ( c,0 \right ),\, F’\left (-c,0 \right )\]
Asse trasverso e asse non trasverso: \[\overline{AA’}=2a,\, \, \overline{BB’}=2b\]
Semiasse trasverso e seminasse non trasverso: \[\overline{OA}=a,\, \, \overline{OB}=b\]
Distanza e semidistanza focale:\[\overline{FF’}=2c,\, \, \overline{OF}=c\]
Uguaglianza fondamentale: \[c^{2}=a^{2}+b^{2}\]
Asintoti: \[y=\frac{b}{a}x,\, \, \, y=-\frac{b}{a}x\]
Eccentricità: \[e=\frac{c}{a}>1\]
Disuguaglianza fondamentale: \[c>a\]
Esempio 1.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’iperbole d’equazione \[\frac{x^{2}}{4}-\frac{y^{2}}{9}=1\]
Si tratta di un’iperbole canonica con i fuochi sull’asse x. Si ha: \[a^{2}=4\Rightarrow a=\pm 2,\, \, b^{2}=9\Rightarrow b=\pm 3\]
e quindi i vertici reali sono \[A\left ( 2,0 \right ),A’\left (- 2,0 \right )\], mentre i vertici immaginari sono \[B\left ( 0,3 \right ),B’\left (0,-3 \right )\] Di conseguenza applicando l’uguaglianza fondamentale si ha:\[c^{2}=a^{2}+b^{2}=4+9=13\rightarrow c=\sqrt{13}\]…F e F’…
Gli asintoti sono \[y=\frac{b}{a}x\rightarrow y=\frac{3}{2}x,\, \, y=-\frac{b}{a}x\rightarrow y=-\frac{3}{2}x,\]…
L’eccentricità è: \[e=\frac{c}{a}=\frac{\sqrt{13}}{2}\]
Esempio 2.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi, la distanza focale e gli asintoti dell’iperbole d’equazione \[\frac{x^{2}}{25}-\frac{y^{2}}{16}=1\]
Esempio 3.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi, la distanza focale e gli asintoti dell’iperbole d’equazione \[\frac{2x^{2}}{3}-\frac{4y^{2}}{5}=7\]
Esempio 4.- Per quali valori del parametro m l’equazione $\frac{x^{2}}{2m-1}+\frac{y^{2}}{m^{2}-4}=1$ è una iperbole con i fuochi sull’asse x o sull’asse y. Per quale valore del parametro m ha un fuoco d’ascissa x = 2?
Iperbole traslata
\[\frac{(x-\alpha)^{2} }{a^{2}}-\frac{(y-\beta )^{2} }{b^{2}}=1\]
centro di simmetria $\displaystyle O’\left ( \alpha ,\beta \right )$. Vedi anche Metodo di completamento dei due quadrati.
Iperbole equilatera e iperbole riferita agli asintoti – Funzione omografica.
Equazione dell’iperbole canonica con i fuochi sull’asse y
Equazione: \[-\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\] oppure \[\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=-1\]
Vertici: \[A\left ( a,0 \right ),\, \, A’\left ( -a,0 \right ),\, \, B\left ( 0,b \right ),\, \, B’\left ( 0,-b \right )\]
Fuochi: \[F\left ( o,c \right ),\, F’\left (0,-c \right )\]
Asse non trasverso e asse trasverso: \[\overline{AA’}=2a,\, \, \overline{BB’}=2b\]
Semiasse non trasverso e seminasse trasverso: \[\overline{OA}=a,\, \, \overline{OB}=b\]
Distanza e semidistanza focale:\[\overline{FF’}=2c,\, \, \overline{OF}=c\]
Uguaglianza fondamentale: \[c^{2}=a^{2}+b^{2}\]
Asintoti: \[y=\frac{b}{a}x,\, \, \, y=-\frac{b}{a}x\]
Eccentricità: \[e=\frac{c}{b}>1\]
Disuguaglianza fondamentale: \[c>b\]
Esempio 1.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’iperbole d’equazione \[\frac{x^{2}}{8}-\frac{y^{2}}{7}=-1\]
Si tratta di un’iperbole canonica con i fuochi sull’asse y. Si ha: \[a^{2}=8\rightarrow a=\pm \sqrt{8}=\pm 2\sqrt{2},\, \, \, b^{2}=7\rightarrow b=\pm \sqrt{7}\]
Esempio 2.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale e gli asintoti dell’iperbole d’equazione \[\frac{x^{2}}{4}-\frac{y^{2}}{9}=-1\]
Esempio 3.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi e la distanza focale dell’iperbole d’equazione \[\frac{3x^{2}}{7}-y^{2}=-1\]
Puoi consultare degli esercizi svolti sul mio canale Youtube.
Iperbole traslata
\[\frac{(x-\alpha)^{2} }{a^{2}}-\frac{(y-\beta )^{2} }{b^{2}}=-1\]
centro di simmetria $\displaystyle O’\left ( \alpha ,\beta \right )$.
Esempio 4.- Determinare i vertici, i fuochi, l’eccentricità la misura degli assi e dei semiassi, la distanza focale e gli asintoti dell’iperbole d’equazione
\[\frac{(x-3)^{2} }{4}-\frac{(y-4 )^{2} }{9}=-1\]
