a) L’equazione di una circonferenza (fig. 1) è: \[x^{2}+y^{2}+ax+by+c=0\] con \[a^{2}+b^{2}-4c\geq 0.\] Se
\[a^{2}+b^{2}-4c=0\] la circonferenza degenera in un punto.
Il centro \[C\left ( x_{c},y_{c} \right )\] della circonferenza ha coordinate:\[x_{c}=-\frac{a}{2},\, \, y_{c}=-\frac{b}{2}\] Il raggio R della circonferenza si può determinare con la formula:\[R=\frac{1}{2}\sqrt{a^{2}+b^{2}-4c}\].
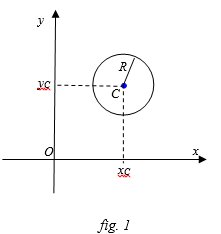
L’equazione della circonferenza di centro \[C\left ( x_{c},y_{c} \right )\, \, e\, \, raggio\, R\] è:\[\left ( x-x_{c} \right )^{2}+\left ( y-y_{c} \right )^{2}=R^{2}\]
b) L’equazione della circonferenza con il centro sull’asse x è: \[x^{2}+y^{2}+by+c=0\]
c) L’equazione della circonferenza con il centro sull’asse y è: \[x^{2}+y^{2}+ax+c=0\]
d) L’equazione della circonferenza con il centro nell’origine O(0,0) e raggio \[R=\sqrt{-c}\]
è: \[x^{2}+y^{2}+c=0\]
e) L’equazione della circonferenza con il centro in O(,00) e raggio R = 1 è:\[x^{2}+y^{2}=1\]
Esempio 1. Data la circonferenza \[x^{2}+y^{2}+4x-6y+1=0\] determinare il suo centro C e il suo raggio R.
Il centro C ha coordinate \[x_{c}=-\frac{a}{2}=-\frac{4}{2}=-2,\, \, \, y_{c}=-\frac{b}{2}=-\frac{-6}{2}=3,\] mentre il raggio R è:\[R=\frac{1}{2}\sqrt{4^{2}+\left ( -6 \right )^{2}-4\cdot \left ( 1 \right )}=\frac{1}{2}\sqrt{48}=2\sqrt{3}\]
Puoi consultare altri esercizi svolti di Geometria Analitica nel mio canale Youtube
