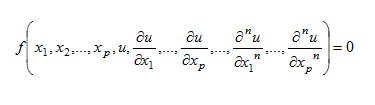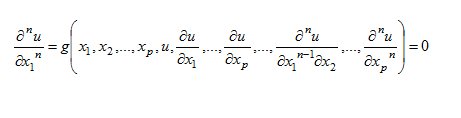Definizione 1
Sia u = u(x, y) una funzione reale di due variabili reali reale.
Si dice equazione differenziale del primo ordine alle derivate parziali un’equazione del tipo:
1)
ove sono le derivate parziali del primo ordine della funzione u rispettivamente rispetto alla variabile x e alla variabile y.
La funzione f è una funzione di cinque variabili reali cioè di .
L’insieme di tute le soluzioni (integrali) dell’equazione differenziale si dice integrale generale (sono esclusi alcuni particolari integrali, detti singolari).
L’equazione si dice scritta in forma normale se è risolta rispetto ad una delle derivate parziali.
La definizione 1 si può generalizzare al caso di una funzione di n variabili indipendenti.
Se u = u( x1, x2 , … , xn ) è una funzione di n variabili reali, si dice equazione differenziale del primo ordine alle derivate parziali un’equazione del tipo:
2)
ove è la derivata parziale del primo ordine rispetto alla variabile indipendente
.
La funzione f è una funzione di 2n + 1 variabili reali cioè di .
Analoghi modi di dire valgono in questo caso.
Definizione 2
Data una funzione , con k sufficientemente grande, si dice equazione differenziale alle derivate parziali d’ordine n un’equazione del tipo
ove è la funzione incognita che si vuole soddisfi l’equazione (3).
Una funzione si dice soluzione o integrale della (3) se la soddisfa identicamente.
L’equazione si dice in forma normale se è risolta rispetto ad una delle derivate parziali di ordine massimo. Ad esempio se è risolta rispetta alla derivata parziale d’ordine n rispetto alla variabile :