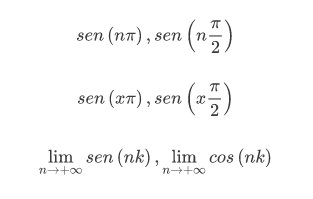
Qui presento alcuni errori molto comuni nel calcolo di un limite, riprendendo qualche esempio dall’interessante libro di esercizi di Renato Fiorenza, “Esercitazioni di analisi matematica”, primo volume, Liguori Editore, libro che consiglio vivamente, ed altri ricercati in rete o in cui mi sono imbattuto negli anni.
In preparazione
Esempio 1.- Calcolare i seguenti limiti: \[sen\left ( n\pi \right ), sen\left ( n\frac{\pi }{2} \right )\]
\[sen\left ( x\pi \right ), sen\left ( x\frac{\pi }{2} \right )\]
\[\lim_{n\rightarrow+\infty }sen\left ( nk \right ),\lim_{n\rightarrow+\infty }cos\left ( nk \right )\]
Risoluzione
Ricordiamo che la successione $\displaystyle a_{n}=sen(n x)$ converge se e solo se $\displaystyle x=k\pi ,\, \, \, \, k\in Z$. Quindi converge $\displaystyle sen\left ( n\pi \right )$ essendo k = 1, mentre non converge $\displaystyle sen\left ( n\frac{\pi }{2} \right )$ perché $\displaystyle k= \frac{1}{2}\notin Z$.
Esempio 2.- Calcolare i seguenti limiti:
\[\lim_{n}n^{2}sen\left ( n\frac{\pi}{2} \right ),\, \, \lim_{n}\left ( n+2 \right )sen\left ( n\frac{\pi}{2} \right ),\, \, \lim_{n}\frac{3^{n}sen\left ( \frac{n\pi }{2} \right )}{2^{n}}\]
\[\lim_{n}cos\left ( \pi -\frac{1}{n} \right ),\, \, \, \lim_{n}cos\left ( n\pi \right ),\, \, \, \lim_{n}nsen\left ( \pi +\frac{1}{n} \right )\]
Risultati: non esiste, non esiste, non esiste, -1, non esiste, -1.
Esempio 3.- Calcolare i seguenti limiti:
\[\lim_{n}\frac{1}{n}sen\frac{n\pi }{2},\, \, \lim_{n}nsen\frac{2 }{n},\, \, \lim_{n}nsen\left ( n\pi \right )\]
Risultati: 0, 2, 0.
Esempio 4.- Calcolare i seguenti limiti di successioni:
1) $\displaystyle sen\left ( \pi \sqrt{4n^{2}+n+1}-2n\pi \right )$
2) $\displaystyle sen\left ( \pi \sqrt{4n^{2}+n+1} \right )$
\[sen\left ( \pi \sqrt{2n^{2}-3n+1} \right ),sen\left ( \pi \frac{n^{2}\left ( n-1 \right )-3}{n} \right )\]
\[sen\left ( 2\pi \sqrt{n^{2}+\sqrt{n}} \right )\]
\[sen\left ( \pi \sqrt[3]{3-t} \right )\]
\[sen\left ( \pi \sqrt{3-t} \right )\]
\[2nsen\left ( \frac{2\pi n^{2}}{n+2} \right )\]
Risoluzione
Il limite (1) vale $\displaystyle \frac{\sqrt{2}}{2}$, il che si vede mettendo in evidenza $\displaystyle \pi$ passando al limite della successione e razionalizzando, ovvero moltiplicando e dividendo per $\displaystyle \sqrt{4n^{2}+n+1}+2n$. Per quanto riguarda il limite (2), si potrebbe pensare di calcolarlo utilizzando la periodicità del seno, ovvero sfruttare la seguente identità
\[sen\left ( \pi \sqrt{4n^{2}+n+1} \right )=sen\left ( \pi \sqrt{4n^{2}+n+1}+2k\pi \right ),\, \, \, k\in Z\]
e pensare di poter scambiare $\displaystyle k\in Z$ con $\displaystyle -n$ passare alla seguente identità
\[sen\left ( \pi \sqrt{4n^{2}+n+1} \right )=sen\left ( \pi \sqrt{4n^{2}+n+1}-2n\pi \right )\]
e poi di calcolare il limite su n. Tale approccio è errato, anche se qualcuno (amministratore e moderatori) in qualche gruppo di matematica ha affermato il contrario. Il punto è che k non è la variabile n e non si può interpretare come n, n è la variabile della successione indicata, k è un valore fisso di volta in volta. Se anche k fosse una variabile della successione staremmo considerando una successione (funzione) di due variabili. Pertanto non ha senso calcolare il limite (2) utilizzando l’identità suddetta e passare al limite (1); il limite (1) esiste e vale $\displaystyle \frac{\sqrt{2}}{2}$, ma non il limite (2). Per calcolare il limite (2)…
Esempio 5.- Calcolare il seguente limite:
\[\lim_{x\rightarrow 0}\frac{\left ( 1+senx \right )2^{x}-1}{x}\]
Questo limite è tratto dal libro indicato sopra. Il limite si presenta nella forma indeterminata 0/0. Si potrebbe pensare di risolverlo osservando che per x che tende a zero il fattore in parentesi tende a 1 e dunque resta il limite notevole \[\lim_{x\rightarrow 0}\frac{2^{x}-1}{x}=ln\, 2\] Di conseguenza si potrebbe pensare di sostituire nel limite assegnato 1 al posto di (1 + sen x) e ottenere come risultato ln 2, ed è sbagliato il risultato e il ragionamento. Il ragionamento è sbagliato per aver sostituito meccanicamente 1 a (1 + sen x) senza aver utilizzato un teorema che lo permetta. La sostituzione sarebbe lecita se il limte fosse $\displaystyle \lim_{x\rightarrow 0}\left ( 1+senx \right )2^{x}$ ma nel caso in esame il limite si riferisce a tutta la frazione, e tale frazione \[\frac{(1+senx)2^{x}-1}{x}\]
non è equivalente a $\displaystyle \left ( 1+senx \right )2^{x}$. Infatti la frazione si presenta in forma indeterminata e dunque il limite del rapporto non si può applicare.
Un altro modo di procedere potrebbe essere quello di sostituire 1 alla potenza $\displaystyle 2^{x}$, per x che tende a zero, e poi applicare il limite notevole senx/x che tende ad 1, Ma tale ragionamento è ancora errato:
$\displaystyle \lim_{x\rightarrow 0}\frac{\left ( 1+senx \right )2^{x}-1}{x}=\lim_{x\rightarrow 0}\frac{1+senx-1}{x}=\lim_{x\rightarrow 0}\frac{senx}{x}=1$.
Il limite in realtà vale (1+ ln 2) e si calcola correttamente come applicazione dei limiti notevoli:
\[\lim_{x\rightarrow 0}\frac{\left ( 1+senx \right )2^{x}-1}{x}=\lim_{x\rightarrow 0}\frac{2^{2}+2^{x}senx-1}{x}=\lim_{x\rightarrow 0}\frac{\left ( 2^{x} -1\right )+2^{x}senx}{x}=\lim_{x\rightarrow 0}\left ( \frac{2^{x}-1}{x} +\frac{2^{x}senx}{x}\right )=\lim_{x\rightarrow 0}\frac{2^{x}-1}{x}+\lim_{x\rightarrow 0}2^{x}\lim_{x\rightarrow 0}\frac{senx}{x}=ln2+1\]
Questo esempio vuole ricordare che per calcolare un limite non bisogna procedere meccanicamente ma di riferirsi sempre ad un teorema matematico. In pratica, prima applicare i teoremi sui limiti se applicabili e poi in base alla forma indeterminata trovata trasformare la funzione in un altra equivalente senza alterare il limite. Porre attenzione nella trasformazione della funzione assegnata in un’altra equivalmente, il che permette di calcolare il limite della funzione trasformata in luogo del limite della funzione assegnata. Può anche accadere che il limite assegnato non esiste o che in realtà solo in apparenza non esista, e allora valutare bene le trasformazioni da fare onde mantenere sempre l’equivalenza tra la funzione assegnata e la funzione trasformata.
Esempio 6.- Calcolare i seguenti limiti:
\[\lim_{x\rightarrow 0}\frac{\left ( cosx \right )4^{x}-1}{x}\]
\[\lim_{x\rightarrow +\infty}\left ( 5^{\frac{1}{x}}\sqrt{x^{2}+x+2}-x \right )\]
Risultati:
Esempio 7.- Calcolare i seguenti due limiti \[\lim_{x\rightarrow 1}\sqrt{x-1},\, \, \, \lim_{x\rightarrow 1}\sqrt{1-x}\]
