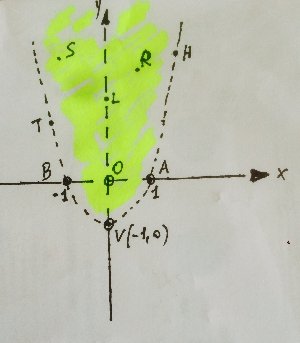
Risoluzione
Bisognare richiedere che il radicando sia positivo e che il denominatore della seconda frazione non sia nullo: \[\left\{\begin{matrix} y-x^{2}+1 &>0 \\ xy^{3} &\neq 0 \end{matrix}\right.\] ossia: \[\left\{\begin{matrix} y>x^{2}-1 \\ \, \, \, \, \, \, x\neq 0\cup y\neq 0 \end{matrix}\right.\] Pertanto il dominio della funzione è l’insieme \[D=\left \{ \left ( x,y \right )\in R^{2}:y>x^{2}-1\, \, e\, \, x\neq 0,y\neq 0 \right \}\] rappresentato nella figura ed evidenziato in giallo.
Notiamo che i punti delle rette x = 0 e y = 0 e della parabola \[y=x^{2}-1\]
non appartengono al dominio della funzione.
Ad esempio i punti A, B, V, L, H, T, O(0,0) non appartengono al dominio della funzione, mentre i punti R, S appartengono al dominio della funzione.