Risoluzione
La variabile casuale X = { punti sulla faccia superiore del dado } può assumere i valori {1, 2, 3, 4, 5, 6} e ognuno con probabilità p = 1/6.
La tabella di distribuzione di probabilità della variabile casuale X è la seguente:

Ricordato che \[\mu=M\left ( X \right ) =\frac{1+n}{2}\] ed \[Var\left ( X \right ) =\frac{n^{2}-1}{12}\] essendo n = 6 e p = 1/6 si ha che:
\[\mu =\frac{1+6}{2}=3.5,\, \, Var(X)=\frac{6^{2}-1}{12}=\frac{35}{12}=2.02\]
Esempio 2.- Distribuzione di Bernoulli o binomiale. Un’urna contiene 15 palline di cui 5 rosse e 10 verdi. Calcolare la probabilità che estraendo 6 palline, reimmettendo ogni volta la pallina estratta nell’urna, 5 siano rosse. Calcolare inoltre, il valore medio e la varianza.
Risoluzione
L’evento E, ossia l’evento che estraendo una pallina dall’urna sia rossa, ha probabilità di verificarsi ad ogni estrazione uguale a:
\[p(E)=\frac{5}{15}=\frac{1}{3}\]
mentre la probabilità dell’evento contrario ad E, indicato con $\displaystyle \overline{E}$, ossia dell’evento che ad ogni estrazione la pallina sia verde, è:
$\displaystyle q\left (\overline{E} \right )=1-p(E)=1-\frac{1}{3}=\frac{2}{3}$
Pertanto, la probabilità che su 6 estrazioni 5 volte venga estratta una pallina rossa, è:
\[p_{6,5}=\binom{6}{5}\left ( \frac{1}{3} \right )^{5}\left ( \frac{2}{3} \right )^{6-5}=\frac{6!}{5!(6-5)!)}\cdot \frac{1}{243}\cdot \frac{2}{3}=\] \[=6\cdot \frac{1}{243}\cdot \frac{2}{3}=0,0164\]
Il valore medio e la varianza sono:
\[\mu =M\left ( X \right )=6\cdot \frac{1}{3}=2\] \[Var\left ( X \right )=6\cdot \frac{1}{3}\cdot \frac{2}{3}=\frac{4}{5}=1,\overline{3}\]
Prova a vedere il video se non sai cosa fare.
Esempio 3.- Una variabile casuale gaussiana ha valor medio 70 e scarto quadratico medio uguale a 12. Calcolare la probabilità che assuma un valore non superiore a 88.
Risoluzione
Si vuol calcolare $\displaystyle Pr(X\leq 88)$; non potendo utilizzare direttamente la
gaussiana standardizzata occorre trasformare il valore $\displaystyle X=88$ nel corrispondente standardizzato con la trasformazione \[Z=\frac{X-\mu }{\sigma }\] Tenuto conto che $\displaystyle \mu =70,\, \, \sigma =12$ si ha:
\[X=88\rightarrow Z=\frac{88-70}{12}=1,5\]
Di conseguenza si ha: \[Pr(X\leq 88)=Pr(Z\leq 1,5)=0,9332\]
Esempio 4.- Un gruppo di 12000 persone si distribuiscono, in base all’altezza, secondo la variabile aleatoria normalizzata (gaussiana). Sapendo che il valore medio è 172 cm e varianza 25 cm, calcolare:
a) la probabilità che l’altezza di una persona scelta a caso sia compresa tra 168 cm e 175 cm;
b) quante persone hanno un’altezza almeno di 178 cm;
c) quante persone hanno un’altezza non superiore a 164 cm.
Risoluzione
Il problema assegna una variabile normale non standardizzata e quindi come prima passo occorre considerare la corrispondente variabile standardizzata.
Essendo $\displaystyle \mu =172,\, \, \sigma^{2} =25\Rightarrow \sigma =5$ , si ha la trasformazione:
\[Z=\frac{X-172}{5}\]
che rappresenta la variabile standardizzata.
a) Mediante questa trasformazione calcoliamo i valori standardizzati corrispondenti a $\displaystyle X_{1}=168 \, \, e\,\, X_{2}=175$ , e si ha:
\[X_{1}=168\rightarrow Z_{1}=\frac{168-172}{5}=-0,8\]
\[X_{2}=175\rightarrow Z_{2}=\frac{175-172}{5}=0,6\]
Pertanto, la probabilità richiesta nel punto a) è data da:
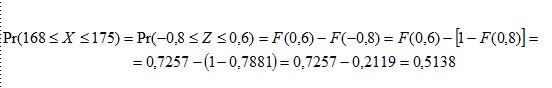
ove i valori
![]()
si calcolano in base alla seguente tabella di probabilità della gaussiana standardizzata. Osserviamo che essendo negativo il valore $\displaystyle Z_{1}=-0,8$ , ci siamo ricondotti ai dati indicati nella tavola mediante la relazione $\displaystyle F(-0,8)=1-F(0,8)$ .
b) Mediante la trasformazione \[Z=\frac{X-172}{5}\] calcoliamo il valore standardizzato corrispondente a $\displaystyle X=178$. Si ha.
\[Z=\frac{178-172}{5}=1,2\]
Pertanto, la probabilità richiesta nel punto b) è data da:
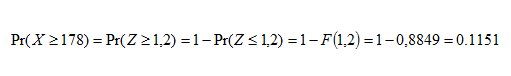
Trasformando in percentuale il valore 0,1151, ossia moltiplicando per 100, si ottiene che 11,51% degli individui ha un’altezza superiore a 178 cm, ossia 1381 persone. Il valore 1381 si calcola eseguendo la percentuale di 12000 (numero degli individui del gruppo), ossia:
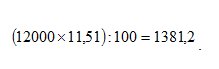
c) Mediante la trasformazione \[Z=\frac{X-172}{5}\] calcoliamo il valore standardizzato corrispondente a $\displaystyle X=164$ . Si ha: \[Z=\frac{164-172}{5}=-1,6\]
Pertanto, la probabilità richiesta nel punto c) è data da:
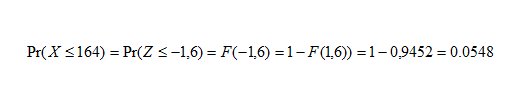
Trasformando in percentuale il valore 0,0548 ossia moltiplicando per 100, si ottiene che 5,48% degli individui ha un’altezza non superiore a 164 cm, ossia 657,6 persone.
Esempio 5.- Un gruppo di 2000 persone si distribuiscono, in base al peso, secondo la variabile aleatoria normalizzata (gaussiana). Sapendo che il valore medio è 72 Kg e varianza 16 Kg, calcolare:
a) la probabilità che il peso di una persona scelta a caso sia compreso tra 66 Kg e 78 Kg;
b) quante persone hanno un peso di almeno di 80 Kg;
c) quante persone hanno un peso non superiore a 68 Kg.
Per questa volta ti faccio uno scherzo e ti chiedo di risolvere, senza il mio aiuto!
Solo ti dico che basta procedere come nell’esercizio precedente. Lo so che ti divertirai un mondo a risolvere l’esercizio!
