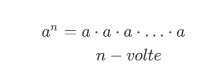 Definizione di potenza nell’insieme dei numeri naturali e razionali positivi. Si dice potenza di base a ed esponente n il prodotto della base a per se stessa tante volte per quanto indicato dall’esponente n:
Definizione di potenza nell’insieme dei numeri naturali e razionali positivi. Si dice potenza di base a ed esponente n il prodotto della base a per se stessa tante volte per quanto indicato dall’esponente n:
\[\begin{matrix} a^{n}=a\cdot a\cdot a\cdot …\cdot a\\ \, \, \, \, \, \, \, \, \, \, \, n-volte \end{matrix}\]
Potenza di una frazione. Se la base a della potenza è una frazione positiva si può dare una definizione di potenza analoga alla precedente e si può utilizzare la seguente proprietà per i calcoli
\[\left ( \frac{a}{b} \right )^{n}=\frac{a^{n}}{b^{n}}\]
Esempio 1.-
\[3^{5}=3\cdot 3\cdot 3\cdot 3\cdot 3=243\]
\[7^{2}=7\cdot 7=49\]
\[\begin{matrix} 2^{123}=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot …\cdot 2=…\\ \, \, \, \, \, \, 123-volte \end{matrix}\]
\[\left ( \frac{6}{7} \right )^{8}=\frac{6^{8}}{7^{8}},\, \, \, \, \left ( \frac{1}{23} \right )^{27}=\frac{1^{27}}{23^{27}}=\frac{1}{23^{27}}\]
Osservazione.- Analoghe regole sussistono se la base della potenza è un numero intero (positivo o negativo), o una frazione positiva o negativa. In breve basta ricordare che bisogna elevare a potenza anche il segno del numero intero o della frazione:
\[\left ( -3 \right )^{4}=+3^{4}=+81,\, \, \left ( -2 \right )^{5}=-2^{5}=-32\]
\[\left ( +4 \right )^{2}=+4^{2}=+16,\, \, \left ( +5 \right )^{3}=+5^{3}=+125\]
\[\left ( -\frac{3}{4} \right )^{2}=+\left ( \frac{3}{4} \right )^{2}=+\frac{9}{16},\, \, \left ( -\frac{5}{2} \right )^{3}=-\left ( \frac{5}{2} \right )^{3}=-\frac{125}{8}\]
\[\left ( +\frac{1}{4} \right )^{2}=+\left ( \frac{1}{4} \right )^{2}=+\frac{1}{16},\, \, \left ( +\frac{3}{2} \right )^{3}=+\left ( \frac{3}{2} \right )^{3}=+\frac{27}{8}\]
Proprietà delle potenze
\[a^{0}=1,0^{0}\, non\, ha\, senso, a^{1}=a, 0^{n}=0, 1^{n}=1\]
\[a^{-1}=\frac{1}{a},\, \, \, \, a^{-n}=\frac{1}{a^{n}}\]
Proprietà delle potenze con la stessa base
\[a^{n}\cdot a^{p}=a^{n+p},\, \, \, \, a^{n}: a^{p}=a^{n-p},\]
\[\left ( a^{n} \right )^{p}=a^{n\cdot p}\]
Proprietà delle potenze con lo stesso esponente e base diversa
\[a^{n}\cdot b^{n}=\left ( a\cdot b \right )^{n},\, \, \, a^{n}:b^{n}=\left ( a: b \right )^{n}\]
Esempio 2.1.- Semplificare le seguenti espressioni con le potenze:
\[7^{2}\cdot 7^{18}:7\cdot 7^{15},\, \, \, \, 3^{12}:3^{8}\cdot 3^{15}\cdot 3^{1987}\]
\[\left ( 15^{13}\cdot 15^{8} \right )^{6}:15:\left ( 3^{24}\cdot 3^{5}:3^{4} \right )^{25}\]
\[\left ( 162^{413}\cdot 162^{1158} \right )^{6}\cdot 162^{574}:\left ( 6^{243}\cdot 6^{25}:6^{18} \right )^{40}\]
\[\left ( \frac{125}{200} \right )^{342}:\left ( \frac{125}{200} \right )^{142}\cdot \left ( \frac{5}{8} \right )^{50}:\left ( \frac{25}{8} \right )^{250}\]
Esempio 3.1.- Semplificare le seguenti espressioni con le potenze:
\[\left ( -3 \right )^{44}\cdot \left ( -3 \right )^{25}:\left ( -3 \right )^{34}\]
\[\left ( -\frac{2}{3} \right )^{4}\cdot \left ( -\frac{2}{3} \right )^{5}:\left ( -\frac{2}{3} \right )^{6}\]
\[\left ( +\frac{2}{5} \right )^{2}\cdot \left ( -\frac{2}{5} \right )^{3}:\left ( -\frac{2}{5} \right )^{4}\]
\[\left ( -\frac{3}{4} \right )^{-5}\cdot \left (+ \frac{3}{4} \right )^{-2}\]
