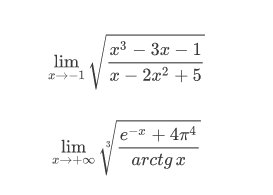
Vogliamo calcolare alcuni limiti di funzioni irrazionali (30 esempi):
- L’esempio 1 mostra come procedere quando sono applicabili i teoremi sui limiti.
- A partire dall’esempio 2 mostriamo limiti che si presentano o in forma indeterminata o come forme convenzionali
di immediata interpretazione.
Esempio 1.1.- Limite calcolato con l’applicazione dei teoremi sui limiti.- Calcolare i seguenti limiti
\[\lim_{x\rightarrow -1 }\sqrt{\frac{x^{3}-3x-1}{x-2x^{2}+5}}\]
\[\lim_{x\rightarrow +\infty }\sqrt[3]{\frac{e^{-x}+4\pi ^{4}}{arctg\, x}}\]
Non sai calcolare il limite? Allora vedi il mio video su Youtube
\[\lim_{x\rightarrow 0 }\sqrt[4]{\frac{ln(x+1)-log_{2}(x+4)}{x-1}}\]
\[\lim_{x\rightarrow 0 }\left [\left ( x+2 \right )^{2}log_{3}(x+24)-\frac{\sqrt{x+16}}{\sqrt[3]{x+1}} \right ]\]
\[\lim_{x\rightarrow \frac{\pi }{2} }\left [\left ( senx+2 \right )^{3}-\frac{\sqrt[3]{cosx+1}}{2x} \right ]\]
Esempio 2.1- Forme convenzionali di immediata interpretazione.- \[\lim_{x\rightarrow +\infty }\sqrt{\frac{e^{-x}-1}{sen\left ( \frac{1}{x} \right )-8}}\] \[\lim_{x\rightarrow 0 }\sqrt[4]{\frac{e^{\frac{1}{x}}-2x+3}{\left | x-1 \right |^{2}}}\]
Risoluzione
Si ha: \[\lim_{x\rightarrow +\infty }\sqrt{\frac{e^{-x}-1}{sen\left ( \frac{1}{x} \right )-8}}=\sqrt{\frac{e^{-\infty }-1}{sen\left ( \frac{1}{+\infty } \right )-8}}=\sqrt{\frac{0-1}{0-8}}=\sqrt{\frac{1}{8}}=\frac{\sqrt{2}}{4}\]
Per calcolare il secondo limite dobbiamo distinguere due casi: \[\lim_{x\rightarrow0^{+} }\sqrt[4]{\frac{e^{\frac{1}{x}}-2x+3}{\left | x-1 \right |^{2}}}=\sqrt[4]{\lim_{x\rightarrow 0^{+}}\frac{e^{\frac{1}{x}}-2(x)+3)}{\left | x-1 \right |^{2}}}=\sqrt[4]{\frac{e^{\frac{1}{0^{+}}}-2(0)+3}{\left | 0-1 \right |^{2}}}=\sqrt[4]{+\infty }=+\infty\]
\[\lim_{x\rightarrow0^{-} }\sqrt[4]{\frac{e^{\frac{1}{x}}-2x+3}{\left | x-1 \right |^{2}}}=\sqrt[4]{\lim_{x\rightarrow 0^{-}}\frac{e^{\frac{1}{x}}-2(x)+3)}{\left | x-1 \right |^{2}}}=\sqrt[4]{\frac{e^{\frac{1}{0^{-}}}-2(0)+3}{\left | 0-1 \right |^{2}}}=\sqrt[4]{\frac{0-0+3}{1} } =\sqrt[4]{3}\]
Pertanto il limite assegnato in zero non esiste, ma esistono i limiti sinistro e destro.
Esempio 2.2.- Calcolare i seguenti limiti \[\lim_{x\rightarrow 3}\sqrt[4]{\frac{\left | x-3 \right |}{x^{2}-3x}}\]
Non sai risolvere l’esercizio? Allora vedi il mio video sul mio canale Youtube
Esempio 2.3.- Calcolare i seguenti limiti \[\lim_{x\rightarrow 0 }\frac{arctanx-\sqrt{\left | x-1 \right |}+7x^{2}}{arcsenx-\frac{arcos(x-1)}{x^{4}}}\]
\[\lim_{x\rightarrow 0 }\frac{senhx+\sqrt{coshx}}{(1-5x)arcsenhx}\]
\[\lim_{x\rightarrow +\infty }\left ( 1+\frac{1}{\sqrt{arctanx}} \right )^{\frac{2x^{2}}{arctanx}}\]
Risoluzione
Il primo limite vale:
\[\lim_{x\rightarrow 0 }\frac{arctanx-\sqrt{\left | x-1 \right |}+7x^{2}}{arcsenx-\frac{arcos(x-1)}{x^{4}}}=\frac{0-1+0}{0-\frac{\pi }{0^{+}}}=\frac{-1} {-\infty }=0\]
Il terzo limite si può calcolare nel seguente modo: \[\lim_{x\rightarrow +\infty }\left ( 1+\frac{1}{\sqrt{arctanx}} \right )^{\frac{2x^{2}}{arctanx}}=\lim_{x\rightarrow +\infty }\left ( 1+\frac{1}{\sqrt{arctanx}} \right )^{\lim_{x\rightarrow \infty }\frac{2x^{2}}{arctanx}}=\left ( 1+\frac{1}{\sqrt{\frac{\pi }{2}}} \right )^{\frac{2\left ( +\infty \right )}{\frac{\pi }{2}}}=\left ( 1+\frac{\sqrt{2\pi }}{\pi } \right )^{+\infty }=+\infty\]
Esempio 3.1.- Forme indeterminate o di indecisione.- Calcolare il seguente limite \[\lim_{x\rightarrow 1}\frac{\sqrt{x+1}-\sqrt{2x}}{\sqrt{x}-\sqrt{2-x}}\]
Risoluzione
Il limite assegnato si presenta nella forma indeterminata 0/0. Per calcolare tale limite razionalizziamo il numeratore e il denominatore della frazioine. Si ha:
\[\frac{\sqrt{x+1}-\sqrt{2x}}{\sqrt{x}-\sqrt{2-x}}\cdot \frac{\sqrt{x}+\sqrt{2-x}}{\sqrt{x}+\sqrt{2-x}}\cdot \frac{\sqrt{x+1}+\sqrt{2x}}{\sqrt{x+1}+\sqrt{2x}}\] da cui si ottiene:
\[\frac{(x+1-2x)\left ( \sqrt{x}+\sqrt{2-x} \right )}{\left [ x-\left ( 2-x \right ) \right ]\left ( \sqrt{x+1}+\sqrt{2x} \right )}=\frac{\left ( 1-x \right )\left ( \sqrt{x}+\sqrt{2-x} \right )}{(2x-2)\left ( \sqrt{x+1} +\sqrt{2x}\right )}=-\frac{\sqrt{x}+\sqrt{2-x}}{2(\sqrt{x+1}+\sqrt{2x})}\]
avendo semplificato ( 1- x). Quindi il limite dato vale \[\lim_{x\rightarrow 1}-\frac{\sqrt{x}+\sqrt{2-x}}{2(\sqrt{x+1}+\sqrt{2x})}=-\frac{1+1}{2\left ( \sqrt{2}+\sqrt{2} \right )}=-\frac{1}{2\sqrt{2}}=-\frac{\sqrt{2}}{4}\]
Esempio 3.2.- Calcolare il seguente limite\[\lim_{x\rightarrow 4}\frac{\sqrt{2x+1}-3}{\sqrt{x-2}-\sqrt{2}}\]
Risoluzione
Il limite assegnato si presenta nella forma indeterminata 0/0. Razionalizzando numeratore e denominatore della frazione si ha: \[\frac{\sqrt{2x+1}-3}{\sqrt{x-2}-\sqrt{2}}\cdot \frac{\sqrt{2x+1}+3}{\sqrt{2x+1}+3}\cdot \frac{\sqrt{x-2}+\sqrt{2}}{\sqrt{x-2}+\sqrt{2}}=\frac{2\left ( x-4 \right )\left ( \sqrt{x-2} +\sqrt{2}\right )}{(x-4)\left ( \sqrt{2x+1}+3 \right )}=\frac{2\left ( \sqrt{x-2}+\sqrt{2} \right )}{\sqrt{2x+1}+3}\] avendo semplificato (x – 4). Quindi il limite assegnato vale \[\lim_{x\rightarrow 4}\frac{2\left ( \sqrt{x-2}+\sqrt{2} \right )}{\sqrt{2x+1}+3}=\frac{2\sqrt{2}}{3}\]
Esempio 3.3.- Calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\left ( \sqrt{9x^{2}+3x-1}-\sqrt{9x^{2}+1} \right )\]
Esempio 3.4.- Calcolare i seguenti limiti: a) \[\lim_{x\rightarrow +\infty }\sqrt{x^{2}+3x+7}-x\]
Non sai calcolare il limite? Allora vedi il mio video su Youtube!
b) Calcolare il seguente limite\[\lim_{x\rightarrow -\infty }\sqrt{\frac{-3x^{4}-5x+1}{-27x^{4}-3x^{2}+x-2}}\]
Esempio 3.5.- Calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\frac{8x+5}{\sqrt{4x^{2}+3x+2}}\]
Calcolare il limite anche a meno infinito.
Non sai calcolare il limite? Allora vedi il mio video su Youtube!
Esempio 3.6.- Calcolare il seguente limite \[\lim_{x\rightarrow 3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}\]
Esempio 3.7.- a) Calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\left ( \sqrt{x^{2}+3}-\sqrt{x} \right )\]
Calcolare anche i seguenti limiti
b) \[\lim_{x\rightarrow +\infty }\left ( x+\sqrt[3]{1-x^{3}} \right )\]
c) \[\lim_{x\rightarrow -\infty }\frac{x+2}{\sqrt{x^{2}+x}}\]
d) \[\lim_{x\rightarrow +\infty }\frac{(x+2)^{2}}{x\sqrt{x^{2}+3x-6}}\]
e) \[\lim_{x\rightarrow 0 }\sqrt[3]{\frac{e^{x}-1}{senx}\cdot \frac{1-cosx}{x}\cdot \frac{3x}{x^{3}-x^{2}}}\]
Esempio 3.8.- Calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\frac{x^{2}+5x+3}{5x\sqrt{x}+4}\]
Esempio 3.9.- a) Calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{\sqrt[3]{1+x}-1}{x}\]
Risoluzione
Si tratta di un’applicazione del limite notevole \[\lim_{x\rightarrow 0}\frac{\left ( 1+x \right )^{p}-1}{x}=p,\, \, \forall p\in R\] Infatti si ha: \[\lim_{x\rightarrow 0}\frac{\sqrt[3]{1+x}-1}{x}=\lim_{x\rightarrow 0}\frac{\left ( 1+x \right )^{\frac{1}{3}}-1}{x}=\frac{1}{3}\]
b) Calcolare anche il seguente limite \[\lim_{x\rightarrow 0}\frac{\sqrt[3]{1+9x^{2}}-1}{x^{2}}\]
Esempio 3.10.- Calcolare il seguente limite \[\lim_{x\rightarrow 0 }\frac{\sqrt{x+1}-1}{\sqrt[3]{x+1}-1}\]
Esempio 3.11 .- Calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{\sqrt[5]{1+4senx}-1}{x}\]
Esempio 3.12.- Calcolare il seguente limite \[\lim_{x\rightarrow 1}\frac{\sqrt{1+\left ( x-1 \right )^{2}}-1}{x^{2}-2x+1}\]
Esempio 3.13.- Calcolare il seguente limite\[\lim_{x\rightarrow 0}\frac{\left (\sqrt[4]{1-arctanx}-1 \right )\left ( e^{3x} -1\right )}{xarctanx}\]
