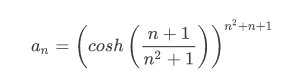
Calcolare i seguenti limiti di successioni
1.- Calcolare il seguente limite \[\lim_{n}\frac{sen^{2}\left ( \frac{1}{n} \right )}{\left ( e^{\frac{1}{2\sqrt{n}}}-1 \right )\cdot ln\left ( 1+\frac{1}{3\sqrt{n^{3}}} \right )}\]
Risoluzione
Il limite vale 6 e si può calcolare con i limiti notevoli nel seguente modo \[\lim_{n}\frac{sen^{2}\left ( \frac{1}{n} \right )\cdot \frac{\frac{1}{n^{2}}}{\frac{1}{n^{2}}}}{\left ( \frac{e^{\frac{1}{2\sqrt{n}}}-1}{\frac{1}{2\sqrt{n}}} \right )\cdot \left ( \frac{1}{2\sqrt{n}} \right )\cdot \left ( ln\left ( 1+\frac{1}{3\sqrt{n^{3}}} \right ) \right )\cdot \frac{\frac{1}{3\sqrt{n^{3}}}}{\frac{1}{3\sqrt{n^{3}}}}}=\lim_{n}\frac{\frac{1}{n^{2}}}{\frac{1}{2\sqrt{n}}\cdot \frac{1}{3\sqrt{n^{3}}}}=\lim_{n}\frac{\frac{1}{n^{2}}}{\frac{1}{6n^{2}}}=6\]
2.- Calcolare il limite della successione \[a_{n}=\left |cos\left ( \frac{n^{2}\pi }{n-3} \right )+sen\left ( \frac{n^{3}\pi }{\left ( n+1 \right )^{2}} \right ) \right |^{\frac{3n^{2}+1}{n+3}}\]
3.- Calcolare il limite della successione \[a_{n}=\frac{1}{n}ln\left ( n! \right )-ln\left ( \frac{n^{2}+2}{n+1} \right )\]
4.- Calcolare il limite della successione \[a_{n}=\left ( cosh\left ( \frac{n+1}{n^{2}+1} \right ) \right )^{n^{2}+n+1}\] Il limite si presenta nella forma indeterminata \[1^{\infty }\]
5.- Calcolare il limite della successione \[a_{n}=\left [ cos\left ( \sqrt{\frac{n+n^{2}}{n^{2}+2n^{3}}} \right ) \right ]^{\frac{n^{3}-1}{n^{2}+1}}\] Il limite si presenta nella forma indeterminata \[1^{\infty }\]
6.- Calcolare il limite della successione \[a_{n}=\left ( \frac{n^{2}+3n+1}{n^{2}-n+3} \right )^{\frac{n^{2}+3}{n+1}}\]
Risoluzione
Il limite si presenta nella forma indeterminata \[1^{\infty }\] e si può calcolare riscrivendo la frazione di base nel seguente modo \[\frac{n^{2}+3n+1}{n^{2}-n+3}=1+\frac{1}{f\left ( n \right )}\] ossia determinando la successione f(n) e quindi riconducendolo al limite notevole \[\lim_{n}\left ( 1+\frac{1}{n} \right )^{n}=e\]
Si ha: \[\frac{4n-2}{n^{2}-n+3}=\frac{1}{f(n)}\Rightarrow f(n)=\frac{n^{2}-n+3}{4n-2}\] e quindi il limite dato diventa\[\lim_{n}\left ( 1+\frac{1}{\frac{n^{2}-n+3}{4n-2}} \right )^{\frac{n^{2}+3}{n+1}\cdot \frac{\frac{n^{2}-n+3}{4n-2}}{\frac{n^{2}-n+3}{4n-2}}}=e^{4}\]
7.- Calcolare il limite della successione \[x_{n}=arctan\left ( \frac{n+1}{n^{2}+3} \right )+\left [ e^{\frac{n+3}{n^{2}+1}} \right ]^{\frac{n^{2}-3}{n-1}}\]
Il primo addendo tende a zero e il secondo si presenta nella forma indeterminata \[1^{\infty }\]
8.- Calcolare il limite della successione \[a_{n}=\left [ \frac{n+3}{n+2}+arctan\left ( \frac{n+2}{n^{2}+3} \right ) \right ]^{\frac{n^{2}+2}{n+3}}\]
Il primo addendo tende a 1 e il secondo tende a zero e quindi il limite si presenta nella forma indeterminata \[1^{\infty }\]
9.- Calcolare il limite della successione \[a_{n}=\left ( \frac{n+cos\left ( \frac{1}{n} \right )}{n-cos\left ( \frac{1}{n} \right )} \right )^{\frac{n+sen\left ( n \right )}{cos\left ( \frac{1}{n} \right )}}\]
10.- Calcolare il limite della successione \[a_{n}=\left ( cos\left ( \frac{\pi n^{2}-3}{n+3} \right ) \right )^{n^{2}}\]
11.- Calcolare il limite della successione \[y_{n}=\left [ cos\left ( \frac{n+1}{n+3} \right )+ln\left ( \frac{n}{n^{4}+2} \right ) \right ]^{\frac{3n^{2}+1}{ln\left ( n^{3}+3 \right )}}\]
12.- Calcolare il limite della successione \[a_{n}=\left [ n\left ( cos\left ( \frac{n^{2}\pi }{n-1} \right )+sen\left ( \frac{n\pi }{n+1} \right )-exp\left ( \frac{2}{n+2} \right ) \right ) \right ]^{\frac{3n+1}{n+3}}\]
13.- Calcolare il limite della successione
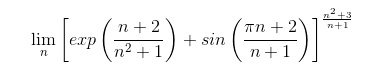
14.- Calcolare il limite della successione \[\lim_{n}\left [ ncos\left ( \frac{\pi n^{2}}{n-1} \right )+sin\left ( \frac{n\pi }{n+1} \right )-exp\left ( \frac{2}{n+2} \right ) \right ]^{\frac{3n+1}{n+3}}\]
15.- Calcolare il limite \[\lim_{n\rightarrow +\infty }\frac{n!}{\left ( 2n+1 \right )!}\]
Risultato L = 0
16.- Calcolare il limite \[\lim_{n\rightarrow +\infty }\left ( n^{2}\int_{0}^{1}\left ( x+1 \right )^{\frac{1}{n}}dx-n^{2} \right )\]
R meno infinito
