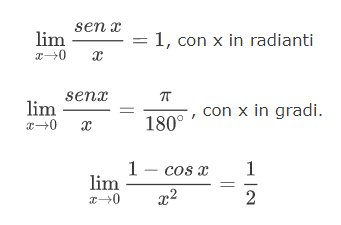
Ricordiamo alcuni limiti notevoli particolarmente importanti:
$\displaystyle \lim_{x\rightarrow 0}\frac{sen\, x}{x}=1$, con x in radianti
$\displaystyle \lim_{x\rightarrow 0}\frac{senx}{x}=\frac{\pi }{180^{\circ}}$, con x in gradi.
\[\lim_{x\rightarrow 0}\frac{1-cos\, x}{x^{2}}=\frac{1}{2}\]
\[\lim_{x\rightarrow 0}\frac{1-cos\, x}{x}=0\]
\[\lim_{x\rightarrow 0}\frac{tan\, x}{x}=1\]
\[\lim_{x\rightarrow 0}\frac{arcsen\, x}{x}=1\]
\[\lim_{x\rightarrow 0}\frac{arctan\, x}{x}=1\]
\[\lim_{x\rightarrow 0}\frac{e^{x}-1}{x}=1\]
\[\lim_{x\rightarrow 0}\frac{a^{x}-1}{x}=ln\, a\]
\[\lim_{x\rightarrow 0}\frac{ln\left ( 1+x \right )}{x}=1\]
\[\lim_{x\rightarrow 0}\frac{log_{a}\left ( 1+x \right )}{x}=log_{a}\, e\]
\[\lim_{x\rightarrow 0}\frac{\left ( 1+x \right )^{\alpha }-1}{x}=\alpha\]
\[\lim_{x\rightarrow +\infty }\left ( 1+\frac{1}{x} \right )^{x}=e\]
\[\lim_{x\rightarrow -\infty }\left ( 1+\frac{1}{x} \right )^{x}=e\]
\[\lim_{x\rightarrow \infty }\left ( 1+\frac{1}{x} \right )^{x}=e\]
\[\lim_{x\rightarrow 0 }\left ( 1+x \right )^{\frac{1}{x}}=e\]
Altri limiti notevoli li puoi trovare nel mio libro “Limiti di funzioni”
Calcolare i seguenti limiti notevoli
Esempio 1.- Calcolare i seguenti limiti \[\lim_{x\rightarrow 0}\frac{sen(\pi \, x)}{x},\, \: \, \lim_{x\rightarrow 0}\frac{sen\, 5x}{x},\, \, \lim_{x\rightarrow 0}\frac{sen\, 3x}{2x},\, \, \lim_{x\rightarrow 0}\frac{sen\, (-6x)}{x},\]
Esempio 2.-Calcolare i seguenti limiti \[\lim_{x\rightarrow 0}\frac{sen\, (6x^{2})}{x^{2}},\, \, \lim_{x\rightarrow 0}\frac{sen\, (x^{2})}{(4x)^{2}},\, \, \lim_{x\rightarrow 0}\frac{sen\, \sqrt{x^{3}}}{x\sqrt{x}},\, \, \lim_{x\rightarrow 0}\frac{sen\, (1-cosx)}{1-cosx}\]
Esempio 3.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{3\, ln\sqrt{1+7x}}{x}\]
Se non riesci a calcolarlo vedi il mio video su Youtube
Prova a risolvere anche questo limite \[\lim_{x\rightarrow 0}\frac{7ln\left ( 1+5x \right )^{2}}{x}\]
Se proprio non riesci puoi trovarlo su Youtube
Esempio 4.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{ln\left ( 1+3x \right )}{e^{^{2x}}-1}\]
Se non riesci a calcolarlo vedi il mio video su Youtube
Esempio 5.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{e^{x}-2^{x}}{x^{2}-2x}\]
Se hai difficoltà consulta il mio video nel mio canale Youtube
Esempio 6.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{1-cos^{3}x}{xsen\, x\cdot cosx}\]
Se hai difficoltà consulta il mio video nel mio canale Youtube
Esempio 7.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{x\, tan2x}{ln(1+7x^{2})}\]
Se hai difficoltà consulta il mio video nel mio canale Youtube
Esempio 8.-Calcolare i seguenti limiti
\[\displaystyle\lim_{x\to 0^{+}}\frac{senx}{\sqrt{1-cosx}}\]
Se non lo sai fare vedi il mio video
\[\lim_{x\rightarrow 0}\frac{1- \sqrt{cosx}}{x^{2}}\]
Se hai difficoltà consulta il mio video nel mio canale Youtube
Esempio 9.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{tan^{2}x-\frac{sen^{2}2x}{4} }{sen^{4}3x}\]
\[\lim_{x\rightarrow\frac{\pi }{4}}\frac{cos2x }{\frac{\pi }{4}-x}\]
\[\lim_{x\rightarrow0}\frac{arcsen\, x }{\left ( 1-cosx \right )^{\frac{1}{2}}}\]
Se non li sai risolvere consulta il mio video
Esempio 10.1.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow +\infty }\frac{ln\left ( \frac{x+1}{x} \right )}{arctanx\cdot arcsen\left ( \frac{1}{x} \right )}\]
\[\lim_{x\rightarrow +\infty }x\cdot ln\left ( \frac{2x+3}{x+2} \right )\cdot sen\left ( \frac{3}{x} \right )\]
\[\lim_{x\rightarrow 0 }\frac{e^{\sqrt{x+1}}-e}{x}\]
Esempio 10.2.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0 }\frac{ln(x+1)+ln(1-x)}{x^{2}}\]
\[ \displaystyle \lim_{ x\to 0}\frac{sen\left ( ln(1+3x^{2}) \right )}{2^{arctanx}-1}\]
\[\lim_{x\rightarrow +\infty }\frac{ln\left ( 1+\frac{1}{x}\right )}{sen{\frac{3}{x}}}\]
\[\lim_{x\rightarrow 0 }\frac{ln\left ( 1+sen^{2}x\right )}{\sqrt{1+x^{2}}-1}\]
\[\lim_{x\rightarrow 0}\left ( \frac{1}{tanx}-\frac{1}{senx} \right )\]
Questo ultimo limite si può calcolare scrivendo la funzione in una unica frazione e dividendo e moltiplicando per x^2, scrivendo poi la tangente del denominatore come senx/cosx,…
Esempio 10.3.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0 }\frac{sen4x\cdot \left [ cos\left ( 3x^{3} \right )-1 \right ]}{ln\left ( 1-x^{3} \right )\cdot tan^{4}x}\]
\[\lim_{x\rightarrow +\infty }\frac{ln\left ( 1+\frac{1}{x} \right )}{sin\frac{3}{x}}\]
\[\lim_{x\rightarrow 0 }\frac{\sqrt{1+x}-1}{ln(1+x)}\]
\[\lim_{x\rightarrow 0 }\frac{sin6x\left ( cos2x-1 \right )}{x}\]
\[\lim_{x\rightarrow +\infty }\frac{ln(2x+2)-ln\left ( 3+x \right )}{6x^{2}}\]
Esempio 10.4.-Calcolare i seguenti limiti
\[\lim_{x\rightarrow 0}\frac{\left ( cosx \right )4^{x}-1}{x}\]
\[\lim_{x\rightarrow +\infty}\left ( 5^{\frac{1}{x}}\sqrt{x^{2}+x+2}-x \right )\]
\[\lim_{x\rightarrow 0^{+}}\frac{x^{senx}-1}{x}\]
\[\lim_{x\rightarrow 0^{+}}\frac{x^{tan^{2}x}-1}{x^{2}}\]
Il risultato è meno infinito.
\[\lim_{x\rightarrow 0}\frac{ln(1+x^{2})-3xsenx+2x^{2}}{\left ( cos(x^{3})-1 \right )^{2}}\]
\[\lim_{x\rightarrow 0}\frac{exp(2x))-2xcos^{2}\left ( \sqrt{x} \right )-1}{ln\left ( \frac{senx}{x} \right )+\frac{x^{3}}{3}}\]
Quest’ultimo limite vale -24
Esempio 11.-Calcolare i seguenti limiti (particolarmente complicati, ma si possono calcolare usando i limiti notevoli, o magari con l’uso della formula di Taylor)
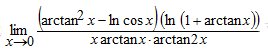
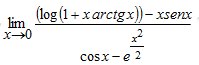
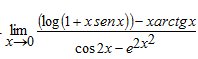
Questi tre esercizi ( svolti con i limiti notevoli) ed altri esercizi svolti li puoi trovare nel mio libro “Limiti di funzioni“
