N.1.- Nel piano Oxy è dato il triangolo rettangolo ABC, con i cateti AB e AC paralleli agli assi x e y rispettivamente e nel quale l’ipotenusa BC e l’altezza ad essa relativa passano per l’origine O del riferimento. Si determini l’equazione del luogo geometrico $\displaystyle \gamma$ descritto dal punto C quando il vertice B percorre la retta x +1 = 0. Si studi e si disegni $\displaystyle \gamma$ che si presenta sotto la forma $\displaystyle y=\pm f(x)$. Si calcoli l’area S della parte finita di piano delimitata da $\displaystyle \gamma$ e dalla retta di equazione x = 1 e si determini il volume V del solido generato dalla rotazione completa di tale regione attorno all’asse delle ascisse.
Risoluzione.
Disegniamo per prima cosa il triangolo ABC, dal testo si intuisce che il vertice A dell’angolo retto si trova nel quarto quadrante, B nel terzo e C nel primo (vedi figura).
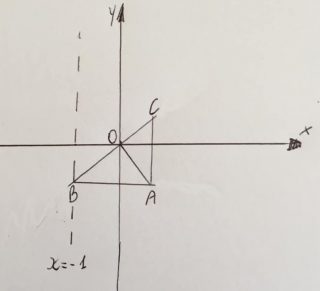
Dato che il punto B percorre la retta x = -1 si capisce che l’ascissa di B è fissa ed è -1, mentre visto che l’ipotenusa BC passa per l’origine O si intuisce che B si trova sulla generica retta y = mx passante per O, e che essendo x = -1 segue che l’ordinata di B è -m: B(-1, – m). Il punto A, essendo AB parallelo all’asse x, ha la stessa ordinata di B, cioè – m. Inoltre, essendo l’altezza OA perperdicolare all’ipotenusa BC, si ha che il vertice A si trova sulla retta $\displaystyle y=-\frac{1}{m}x$, con m coefficiente angolare della retta BC.
Pertanto l’ascissa del punto A è
$\displaystyle y_{A}=-\frac{1}{m}x_{A}\Rightarrow -m=-\frac{1}{m}x_{A}$ cioè $\displaystyle x_{A}=m^{2}$.
Di conseguenza il punto C ha coordinate $\displaystyle x_{C}=m^{2},\, y_{C}=m^{3}$.
In definitiva le equazioni parametriche del luogo richiesto sono $\displaystyle \left\{\begin{matrix} x &=m^{2} \\ y &=m^{3} \end{matrix}\right.$ e ricavando m nella prima equazione e sostituendo nella seconda si ha l’equazione cartesiana del luogo: $\displaystyle y=\pm \sqrt{x^{3}}$
N.2.- Sia $\displaystyle x=\frac{m^{2}}{1+m^{2}},\, y=\frac{m^{3}}{1+m^{2}}$. Si esprima y in funzione di x, si studi e si disegni nel piano Oxy tale funzione che si presenta sotto la forma $\displaystyle y=\pm f(x)$. Si calcoli l’area della regione finita di piano delimitata dalla curva e dalla retta 2x = 1 e si determini il volume V del solido generato dalla rotazione di tale regione attorno all’asse delle ascisse.
N.3.- Nel piano Oxy scritta l’equazione del fascio di rette proprio con centro nel punto C(1,1) si determini l’equazione del luogo dei punti P di intersezione del fascio dato con il fascio costituito dalle infinite rette parallele all’asse delle x e la cui ordinata è uguale al coefficiente angolare delle rette del primo fascio. Dopo aver studiato e rappresentato si calcoli l’area S della porzione finita di piano delimitata dalla curva, dagli assi cartesiani, e dalla retta x = 1 e si determini, infine, il volume V del solito ottenuto dalla rotazione completa di tale regione attorno all’asse delle ascisse.
N.4.- Sia $\displaystyle x=cos\, t,\, y=\frac{cos\, t}{tan\, t}$. Si esprima y in funzione di x, si studi e si disegni nel piano Oxy t ale funzione che si presenta sotto la forma $\displaystyle y=\pm f(x)$ individuando simmetrie e caratteristiche del grafico trovato. Si calcoli l’area S della regione finita di piano delimitata nel primo quadrante dalla curva e dalla bisettrice y = x e si determini il volume V del solido generato dalla rotazione di tale regione attorno al’asse delle ascisse.
N.5.- Secondo problema Sessione Ordinaria 1990.- Determinare il luogo dei centri delle circonferenze tangenti alla retta y = 37/12 e passanti per A(0, 19/12) ed il luogo dei centri delle circonferenze tangenti alla circonferenza di equazione $\displaystyle x^{2}+y^{2}+4x+4y-8=0$ e passanti per B(2,2)
Calcolare quindi l’area della parte dipiano racchiusa dalle due curve.
N.6.- Primo problema Sessione Ordinaria 1991.- In un piano cartesiano ortogonale Oxy si consideri il punto A(2x, 0). Si trovi il luogo L dei punti B(x,y) tale che il triangolo OAB abbia perimetro 2p e si determini l’area della regione finita di piano delimitata dal luogo stesso. Se $\displaystyle B_{0}$ è il punto di L del 1° quadrante la cui ascissa è p/4 ed $\displaystyle A_{0}$ il terzo vertice del relativo triangolo, si calcoli l’area del triangolo $\displaystyle OA_{0}B_{0}$. Si individuino inoltre le altre 7 posizioni di B tali che il triangolo OAB sia equivalente ad $\displaystyle OA_{0}B_{0}$.
N.7.- Sia Oxy un sistema di riferimento cartesiano del piano e $\displaystyle \Gamma$ la circonferenza di centro l’origine O e raggio 4. Detto P un punto di $\displaystyle \Gamma$, sia $\displaystyle \gamma$ la circonferenza di centro P e tangente all’asse x e sia T l’intersezione dell’asse radicale di $\displaystyle \Gamma$ e $\displaystyle \gamma$ con la parallela per P all’asse y. Determinare l’equazione del luogo descrittto da T al variare di P su $\displaystyle \Gamma$.
