 Nel 2021 per la Maturità Scientifica è stato assegnato ad ogni studente o gruppo di studenti un elaboratore personale da consegnare entro il 31 maggio in formato pdf..
Nel 2021 per la Maturità Scientifica è stato assegnato ad ogni studente o gruppo di studenti un elaboratore personale da consegnare entro il 31 maggio in formato pdf..
Liceo Scientifico, Traccia 1.- “Anche le parole che ora diciamo il TEMPO nella sua rapina ha già portato via e nulla torna” ( I, 11) Odi di Orazio..
“Il mistero del tempo ci inquieta da sempre, muove emozioni profonde … La fisica ci aiuta a penetrare strati del
mistero. Mostra come la struttura temporale del mondo sia diversa dalla nostra intuizione. Ci dà la speranza di poter studiare la natura del tempo liberandoci dalla nebbia causata dalle nostre emozioni…” C. ROVELLI – L’ordine del tempo
Il tempo è il movimento delle cose per gli antichi, il tempo è assoluto e scorre indipendentemente dal moto dei corpi per Newton. Poco più di cento anni fa Einstein comprese che il tempo è rallentato dalle masse e circa dieci anni prima aveva compreso che il tempo è rallentato dalla velocità. Il candidato, con riferimento all’argomento indicato, presenti un elaborato nel quale approfondisca il tema, sviluppi l’interazione con la Matematica, integri con apporti di altre discipline o competenze individuali del proprio curriculum, ed eventualmente con l’esperienza maturata nel PCTO.
In particolare, in relazione alle discipline caratterizzanti, lo studente:
- evidenzi i nodi concettuali dell’argomento nell’evoluzione del pensiero scientifico e spieghi: – la dilatazione dei tempi nella relatività ristretta, evidenziando come le trasformazioni di Lorentz prevedano il fenomeno, – la dilatazione gravitazionale dei tempi;
- studi la funzione $\displaystyle \gamma \left ( v \right )=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$, dove $\displaystyle \gamma$ è il coefficiente di dilatazione e discuta, mediante esempi, in modo esaustivo la ricerca degli asintoti del diagramma di una funzione e le discontinuità di una funzione anche senza asintoti;
- discuta un’applicazione inerente all’ argomento, corredata da una valutazione che evidenzi la ricaduta sul progresso;
- costruisca una mappa concettuale che evidenzi i nessi logici tra i punti chiave coinvolti
Risoluzione della parte di matematica e fisica
Per la dilatazione dei tempi in Relatività Ristretta clicca qui
Studio della funzione:
$\displaystyle \gamma \left ( v \right )=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$
Posto v = x e$\displaystyle f =\gamma$ si ha:
$\displaystyle f \left (x \right )=\frac{1}{\sqrt{1-\frac{x^{2}}{c^{2}}}}$
Dominio D:
$\displaystyle \left\{\begin{matrix} \sqrt{1-\frac{x^{2}}{c^{2}}} & \neq 0 & \\ {1-\frac{x^{2}}{c^{2}}} &\geq 0 & \end{matrix}\right.$
da cui:
$\displaystyle 1-\frac{x^{2}}{c^{2}} >0$
e calcolando il delta, otteniamo: $\displaystyle \Delta =4c^{2},\, \, \, x=\pm c$
Pertanto le soluzioni della disequazione sono – c < x < c e il dominio della funzione è l’intervallo $\displaystyle \left ( -c,\, c \right )$.
Calcoliamo i limiti negli estremi del dominio per determinare eventuali asintoti e/o punti di discontinuità.
\[\lim_{x\rightarrow c^{+}}\frac{1}{\sqrt{1-\frac{x^{2}}{c^{2}}}}=\frac{1}{0^{+}}=+\infty\]
\[\lim_{x\rightarrow c^{-}}\frac{1}{\sqrt{1-\frac{x^{2}}{c^{2}}}}=\frac{1}{0^{-}}=+\infty\]
si deduce che le rette x = c e x = – c sono asintoti verticali per la funzione; non esistono punti di discontinuità e asintoti orizzontali o obliqui.
La funzione è positiva, perché rapporto di quantità positive:
\[f(x)>0,\, \, \, \, \forall x\in R\]
Calcoliamo la derivata prima della funzione riscrivendola nel seguente modo:
\[f(x)=\frac{1}{\sqrt{1-\frac{x^{2}}{c^{2}}}}=\frac{c}{\sqrt{c^{2}-x^{2}}}\]
Applicando la regola del rapporto per le derivate si ha:
\[y'(x)=\frac{0\cdot\sqrt{c^{2}-x^{2}}-c\frac{1}{2\sqrt{c^{2}-x^{2}}}(-2x)}{\left ( \sqrt{c^{2}-x^{2}} \right )}=\frac{cx}{\left ( c^{2}-x^{2} \right )\sqrt{c^{2}-x^{2}}}\]
e imponendo la derivata prima maggiore o uguale di zero si ha:
\[y'(x)\geq 0\, \, \, \rightarrow\, \, \, \frac{x}{\left ( c^{2}-x^{2} \right )}\geq 0\]
avendo trascusrato le quantità positive, che ammette per soluzioni 0 ≤ x < c, come si vede richiedendo che il numeratore sia non negativo e il denominatore sia positivo. Pertanto la derivata prima è positiva o nulla nell’intervallo 0 ≤ x < c e in tale intervallo la funzione è crescente, mentre la derivata prima è negativa nell’intervallo – c < x < 0 e in tale intervallo la funzione è crescente (fig. 1); nel punto x = 0 ammette un punto di minimo relativo, di ordinata 1.
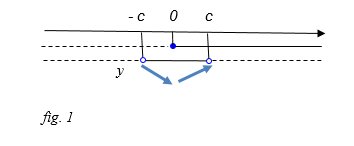
Il grafico della funzione, riportato nella figura 2, ammette un punto di minimo relativo di coordinate (0,1).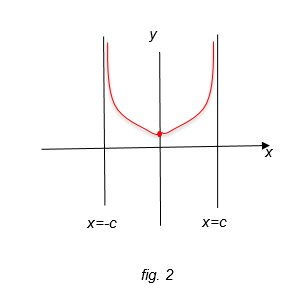
Liceo Scientifico, Traccia 2.- Il candidato, dopo aver introdotto il tema proposto:
- fornisca la definizione di circuito elettrico e ne indichi gli elementi caratteristici;
- si soffermi sul concetto di corrente alternata e operi un confronto tra circuiti in corrente continua e circuiti in corrente alternata;
- descriva le caratteristiche dei circuiti ohmici, capaciti e induttivi, sottolineando la relazione tra tensione alternata e corrente alternata;
- calcoli la forza elettromotrice massima e quella efficace di un generatore di corrente alternata sapendo che la corrente che circola in un condensatore di capacità $\displaystyle 16\cdot 10^{-6}F$ ha il valore massimo di 20 𝐴 e che la frequenza del generatore di tensione alternata è di 50 𝐻𝑧;
- definisca il concetto di massimo e minimo assoluto e relativo di una funzione;
- fornisca la definizione di derivata prima e seconda di una funzione;
- enunci il teorema di Fermat e spieghi come si determinano i massimi e i minimi relativi di una funzione;
- determini il valore del parametro reale 𝑘 affinché la funzione:
$\displaystyle y=\frac{kx^{2}-1}{x+2}$
abbia un massimo nel punto di ascissa 𝑥 = −1 e determini le equazioni degli eventuali asintoti della funzione.
Nota.- Sembra che nella traccia ci sia un errore, che sarà evidenziato successivamente
Liceo Scientifico, Traccia 3.-

Liceo Scientifico, Traccia 4.-
Un circuito RLC in serie è composto da una resistenza di 250 W, una bobina da 3,40 mH e un condensatore da 98,0 nF. Il circuito è collegato ad una alimentazione alternata con una forza elettromotrice massima e una frequenza f = 5,00 k Hz. Determinare l’intensità massima di corrente. Studiare, inoltre, il grafico della funzione i(t) così ottenuta.
Risoluzione
Risoluzione del problema di fisica clicca qui.
Studio e grafico della funzione sinusoidale
La funzione sinusoidale:
\[i(t)=0,042\cdot sen(31400\cdot t+41^{\circ})\]
trasformando 41° in radianti si può scrivere nel seguente modo:
\[i(t)=0,042\cdot sen(31400\cdot t+0,72)\]
Studiamo dunque tale funzione, definita e continua nell’insieme R dei numeri reali, nell’intervallo:
\[\left [ 0,\frac{\pi }{15700}\, \, \right ]\]
poiché periodica di periodo P:
\[p=\frac{2\pi }{31400}=\frac{\pi }{15700}\approx 0,0002\]
La funzione nell’intervallo chiuso e limitato $\displaystyle \left [ 0,\frac{\pi }{15700} \right ]$ non ammette asintoti.
Il segno della funzione si può stabilire determinando gli zeri della funzione e tenendo conto che la funzione seno è continua in tutto R e dunque anche nell’intervallo di periodicità considerato. Gli zeri della funzione che ricadono nell’intervallo di periodicità si possono ottenere risolvendo l’eequazione:
$\displaystyle i(t)=0\, \, \, \rightarrow \, \, \, 0,042sen(31400t+0,72)=0\, \, \rightarrow\, \, sen(31400t+0,72)=0$
da cui tenuto conto che il seno si annulla quando l’argomento è multiplo di $\displaystyle k\pi ,k\in Z$ si hanno i seguenti due zeri della funzione:
$\displaystyle t=\frac{\pi -0,72}{31400}\approx 0,00007707$, $\displaystyle t=\frac{2\pi -0,72}{31400}\approx 0,00017$
il primo ottenuto per k = 1 e il secondo per k = 2. Osserviamo pure che i(0) > 0 e $\displaystyle i\left ( \frac{\pi }{15700} \right )>0$ .
Da tutte queste informazioni si può dedurre che la funzione nell’intervallo $\displaystyle \left [ 0,\frac{\pi }{15700} \right ]$ è positiva per $\displaystyle 0<t<\frac{\pi -0,72}{31400}\, \, \cup\, \, \frac{2\pi -0,72}{31400}<x<\frac{\pi }{15700}$ si annulla nei due zeri indicati ed è negativa altrimenti.
Naturalmente si può stabilire la positività anche risolvendo la disequazione:
\[i(t)=0,042\cdot sen\left ( 31400\cdot t+0,72 \right )\geq 0\, \, \, \rightarrow\, \, \, 0,042\cdot sen\left ( 31400\cdot t+0,72 \right )\geq 0\rightarrow \, \, \, \, sen\left ( 31400\cdot t+0,72 \right )\geq 0\]
da cui posto: $\displaystyle z= 31400\cdot t+0,72$ si ha la disequazione elementare:
\[sen\, z\geq0\]
verificata per $\displaystyle 0\leq z\leq \pi$ e tenuto conto della posizione $\displaystyle z= 31400\cdot t+0,72$ si ha:
$\displaystyle 0\leq 31400\cdot t+0,72\leq \pi$
ossia:
\[-0,72\leq 31400t\leq \pi -0,72\, \, \, \, \, \rightarrow\, \, \, \, \frac{-0,72}{31400}\leq t\leq \frac{\pi -0,72}{31400}\]
con $\displaystyle \frac{\pi -0,72}{31400}=\frac{25\pi -18}{785000}\approx 0,00007707$. Un ulteriore zero della funzione è $\displaystyle \frac{25\pi -9}{392500}\approx 0,00017$.
La funzione inoltre interseca l’asse y = i(t) nel punto di ordinata
$\displaystyle i(0)=0,042sen(0,72)$
con $\displaystyle sen(0,72)\approx 0,013$.
Il valore massimo di tale funzione si ottiene richiedendo che il seno sia massimo, cioè uguale ad 1, il che accade se l’argomento del seno è $\displaystyle \frac{\pi }{2}$:
$\displaystyle 31400\cdot t+0,72=\frac{\pi }{2}$
da cui
\[t=\frac{\frac{\pi }{2}-0,72}{31400}\approx 0,000027\, s\]
Il valore minimo di tale funzione si ottiene richiedendo che il seno sia minimo, cioè uguale -1, il che accade se l’argomento del seno è $\displaystyle \frac{3\pi }{2}$, cioè
\[t=\frac{\frac{3\pi }{2}-0,72}{31400}\approx 0,000127\, s\]
Notiamo che i punti di massimo e di minimo si potevano calcolare anche con l’ausilio della derivata prima imposta maggiore uguale di zero. La derivata prima della funzione i(t) è:
\[i'(t)=0,042\cdot cos\left ( 31400t+0,72 \right )\cdot 31400=1318,8\cdot cos\left ( 31400t+0,72 \right )\]
e risolvendo la disequazione:
\[i'(t)\geq 0\rightarrow \, \, \, 1318,8\cdot cos\left ( 31400t+0,72 \right )\geq 0\]
si perviene agli stessi risultati prima trovati.
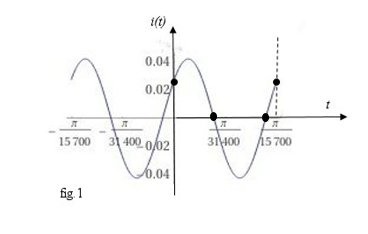
Pertanto la funzione è crescente per … e decrescente altrimenti. Il valore massimo della funzione è:
\[i\left (\frac{\frac{\pi }{2}-0,72}{31400} \right )=i(0,000027)=0,0419\]
Analogamente si procede per calcolare il minimo della funzione:
\[i\left (\frac{\frac{3\pi }{2}-0,72}{31400} \right )=i(0,000127)=-0,0419\]
Il grafico della funzione è rappresentato nella figura 1.
Vuoi preparare la prova di matematica della Maturità Scientifica? Parti da qui allora !
