Sarà più semplice o più complicata di come era negli anni precedenti il 2020? Riguarderà solo argomenti di matematica? o anche di fisica?
Alla fine ci sarà sia matematica che fisica: un problema di matematica, un problema di fisica, e 8 quesiti.
Per preparare la prova scritta di matematica della Maturità Scientifica clicca qui
E finalmente la Maturità 2023 si è svolta ed ecco le prove d’esame. Osservo che chi avesse comprato il mio libro Guida pratica per la prova scritta dellla maturità Scientifica avrebbe trovato il Problema 2 abbastanza facile da svolgere.
Ecco le prove tratte dalla rete: due problemi e 8 quesiti.

Gli 8 quesiti

Risoluzione Problema 2
a)Il dominio della funzione $f(x)=\frac{x^{2}-ax}{x^{2}-a}$ si ottiene imponendo che il denominatore della frazione sia diverso da zero:
\[ x^{2}-a\neq 0\, \Rightarrow\, \, x\neq \pm \sqrt{a}\]
con a >0. Se invece è a < 0 il dominio della funzione è tutto R, perché \[ x^{2}-a\neq 0 \] è sempre diverso da zero. Di conseguenza per a > 0 la funzione si può riscrivere nel seguente modo.
\[ x^{2}-a\neq 0\, \Rightarrow\, \, x\neq \pm \sqrt{a}\]
e per a < 0 resta così:
$f(x)=\frac{x^{2}-ax}{x^{2}-a}$.
Al variare di a la funzione si può scrivere così:
\[f_{a}(x)=\frac{x^{2}-ax}{x^{2}-a}=\left\{\begin{matrix} \frac{x^{2}-ax}{x^{2}-a}\: \: \: \: \: se\, \, a<0 \\ \\ \frac{x^{2}-ax}{\left ( x+\sqrt{a} \right )\left ( x-\sqrt{a} \right )}\, \, se\, a>0\\ \end{matrix}\right. \]
ed è dunque composta da due rami.
Nel caso a > 0 la funzione ammette due asintoti verticali $x=\sqrt{a},\, \, x =-\sqrt{a}$ discontinuità di seconda specie, e un asintoto orizzontale d’equazione y = 1. Il che si vede calcolando i limiti nei punti
$x=\sqrt{a},\, \, x =-\sqrt{a}$
Nel caso a < 0 non ammette asintoti verticali e dunque discontinuità e ammette però soltanto l’asintoto orizzontale y = 1.
b) Per risolvere questo punto basta mettere a sistema l’asintoto comune y = 1 con le due funzioni (quella per a > 0 e quella per a < 0) e calcolare il punto d’intersezione. In entrambi i casi il punto d’intersezione P ha per ascissa x = 1 e ordinata y = 1, P(1,1). Per avere la stessa retta tangente in tale punto O(0,0) basta calcolare la derivata delle due funzioni e verificare che assumono lo stesso valore in x = 0:
\[ f’_{a}(x)=\frac{(2x-a)(x^{2}-a)-\left ( x^{2}-ax \right )2x}{\left ( x^{2}-a \right )^{2}}\]
cioè
\[f’_{a}\left ( x \right )=\frac{ax^{2}-2ax+a^{2}}{\left ( x^{2}-a \right )^{2}}\]
e
\[ f'(0)=1\]
La retta tangente comune nell’origine è y = x.
c) La funzione al variare di a < 1 è composta da due rami, il ramo ottenuto per a < 0 e il ramo ottenuto per 0<a<1:
\[f_{a}(x)=\frac{x^{2}-ax}{x^{2}-a}=\left\{\begin{matrix} \frac{x^{2}-ax}{x^{2}-a}\: \: \: \: \: se\, \, a<0 \\ \\ \frac{x^{2}-ax}{\left ( x+\sqrt{a} \right )\left ( x-\sqrt{a} \right )}\, \, se\, 0<a<1\\ \end{matrix}\right. \]
e la derivata è sempre
\[f’_{a}\left ( x \right )=\frac{ax^{2}-2ax+a^{2}}{\left ( x^{2}-a \right )^{2}}\]
Per studiare la crescenza della funzione risolviamo la disequazione $f'(x)\geq 0$ al variare del parametro a
\[f’_{a}\left ( x \right )\geq 0\rightarrow \frac{ax^{2}-2ax+a^{2}}{\left ( x^{2}-a \right )^{2}}\geq 0\]
da cui consideriamo la disequazione $ax^{2}-2ax+a^{2}\geq 0$ e risolviamola nei due casi richiesti. Si ha.
per a < 0: la funzione è crescente per valori interni all’intervallo delle radici \[1- \sqrt{1-a}<x<1+ \sqrt{1-a}\]
e decrescente altrimenti.
per 0 < a < 1: la funzione è crescente per valori esterni all’intervallo delle radici
\[x<1- \sqrt{1-a}\, \, \, \cup\, \, x>1+ \sqrt{1-a} \]
e decrescente altrimenti
ove le radici sono \[x=\frac{a\pm \sqrt{a^{2}-a^{3}}}{a}=\frac{a\pm \sqrt{a^{2}\left ( 1-a \right )}}{a}=1\pm \sqrt{1-a}\]
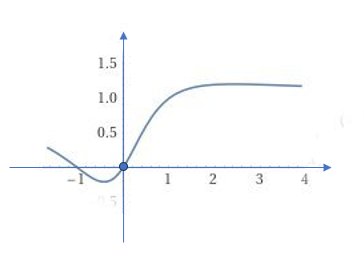
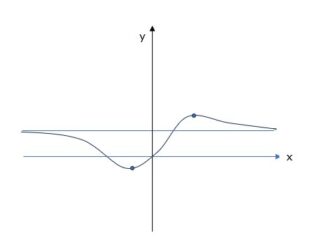
La funzione $f_{-1}(x)$ si ottiene sostituendo a = -1 ed è
\[f_{-1}(x)=\frac{x^{2}+x}{x^{2}+1}\]
che ovviamente ha dominio D = R, si tratta di una funzione continua che ammette solo un asintoto orizzontale y = 1, è positiva per x < -1, x > 0 e negativa per -1< x < 0; interseca l’asse x nei punti (-1, 0) e (0,0). La derivata prima è $ f'(x)=\frac{-x^{2}+2x+1}{\left ( x^{2}+1 \right )^{2}}$, la si ottiene sostituendo a = -1 nella derivata della $f_{a}(x)$. Ammette dunque un minimo per $x=1-\sqrt{2}$ e un massimo relativo per $x=1+\sqrt{2}$:
\[f(1+\sqrt{2})=\frac{1+\sqrt{2}}{2}\]
\[f(1-\sqrt{2})=\frac{1-\sqrt{2}}{2}\]
ammette inoltre tre punti di flesso, i quali si possono determinare calcolando la derivata seconda \[f”(x)=\frac{2\left ( x^{3}-3x^{3}-3x+1 \right )}{\left ( x^{2}+1 \right )^{3}}\], essi sono $x=-1,\: x=2-\sqrt{3},\, x=2+\sqrt{3}$, con \[x^{3}-3x^{2}-3x+1=0\Leftrightarrow (x+1)(x^{2}-4x+1)=0\]
Il grafico è quello rappresentato nella figura:
d) L’area A della regione finita di piano richiesta si può calcolare con la seguente formula: \[ A=Area\, Trapezio-\int_{1}^{\sqrt{3}}\frac{x^{2}+x}{x^{2}+1}dx\]
e l’area del trapezio vale $Area\, Trapezio=\frac{\left ( \sqrt{3} -1\right )\left ( \sqrt{3} +1\right )}{2}=1$, mentre l’integrale si calcola nel seguente modo:
\[\int_{1}^{\sqrt{3}}\frac{x^{2}+x}{x^{2}+1}dx=\int_{1}^{\sqrt{3}}\frac{x^{2}+x+1-1}{x^{2}+1}dx=\int_{1}^{\sqrt{3}}dx+\int_{1}^{\sqrt{3}}\frac{x-1}{x^{2}+1}dx=\int_{1}^{\sqrt{3}}dx+\int_{1}^{\sqrt{3}}\frac{x}{x^{2}+1}dx-\int_{1}^{\sqrt{3}}\frac{1}{x^{2}+1}dx=…\]
con
\[\int_{1}^{\sqrt{3}}dx=\left [ x \right ]_{1}^{\sqrt{3}};\, \, \frac{1}{2}\int_{1}^{\sqrt{3}}\frac{2x}{x^{2}+1}dx=\frac{1}{2}\left [ ln\left ( x^{2}+1 \right ) \right ]_{1}^{\sqrt{3}}\, ;\, \int_{1}^{\sqrt{3}}\frac{1}{x^{2}+1}dx=\left [ arctanx \right ]_{1}^{\sqrt{3}}\]
In definitiva l’area A è:
\[A=1-\left\{ \sqrt{3}-1+\frac{1}{2}\left [ ln\left ( x^{2}+1 \right ) \right ]_{1}^{\sqrt{3}}-\left [ arctanx \right ]_{1}^{\sqrt{3}}\right\}=…=2-\sqrt{3}-ln\sqrt{2}+\frac{\pi }{12}\approx 0,19\]
Ti serve un telefono? Clicca qui