Mosse di cavallo sopra una scacchiera illimitata

Vogliamo determinare il numero minimo di mosse di cavallo per andare da una casella ad un’altra su una scacchiera illimitata. Presentiamo per semplicità inizialmente la questione su una scacchiera limitata.
Sia Oxy un sistema di assi cartesiani ortogonali e S una scacchiera disposta in modo che la casella a1, di lato unitario, abbia due vertici non consecutivi nei punti O(0,0) e P(1,1) ( fig. 1).

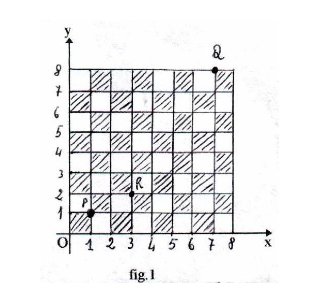
In tal modo, se (x , y), (x₁ , y₁ ), (x₂ , y₂ ), (x₃ , y₃ ) sono le coordinate dei quattro vertici di una generica casella C e x + y la massima delle somme x + y, x₁ + y₁ , x₂ + y₂ , x₃ + y₃, possiamo identificare la casella C con il punto di coordinate (x,y) e parlare di punto in luogo di casella.
In virtù di ciò ogni casella della scacchiera è identificata con un unico punto del piano e ogni mossa di Cavallo è rappresentabile mediante spostamenti paralleli all’asse x e all’asse y.
Ad esempio, la casella a1 è identificata con il punto P(1,1), la casella g8 con il punto Q(7,8); mentre la mossa di Cavallo a1-c2 consiste nel passare dal punto P(1,1) al punto R(3,2): ossia ad uno spostamento di due unità nella direzione positiva dell’asse x e di un’ unità nella direzione positiva dell’asse y.
Pertanto, in generale, il numero di mosse sufficiente perché il Cavallo si porti dal punto S(x₁,y₁) al punto T(x₂,y₂) coincide con il minimo intero positivo n tale che:

x₂ = x₁ + p₁ + p₂ +…..+ p_n     , y₂ = y₁ + q₁ + q₂ +…..+ q_n

x₂ – x₁ = p₁ + p₂ +…..+ p_n , y₂ – y₁ = q₁ + q₂ +…..+ q_n

ove ognuna delle n coppie di numeri interi (p₁ ,q₁),.., (p_n ,q_n), con | p_i | + | q_i | = 3 , i = 1,2,…,n, rappresenta una mossa di Cavallo.
Di conseguenza una successione minima di mosse per andare dal punto S al punto T è nota non appena sono noti i numeri p₁ e q₁ , p₂ e q₂ , … , p_n e q_n .
A tale scopo, introduciamo la seguente:

Definizione. Si dice che la coppia (a, b) di interi positivi ammette una ripartizione, per mosse di Cavallo, di classe n e di termini p₁ , p₂ ,….., p_n , q₁ , q₂ ,….., q_n  ( interi non nulli), se:

a = p₁ + p₂ +…..+ p_n , b = q₁ + q₂+…..+ q_n

con | p_i | + | q_i | = 3 , i = 1,2,…n.
Una tale ripartizione, che non è unica, si indica con il simbolo: 

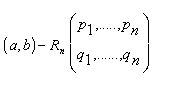
inoltre, si dice primitiva se è di classe minima, ed è determinabile quando è possibile conoscere i suoi termini.
La coppia (4,5) ammette, ad esempio, le ripartizioni:

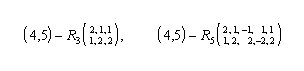
la prima di classe 3 e la seconda di classe 5.
Pertanto la questione in esame si riconduce alla ricerca di una ripartizione primitiva della coppia

(x₂ – x₁ , y₂ – y₁ ),

ove la classe di ripartizione esprime il numero minimo di mosse per passare dal punto S al punto T, e i termini di essa la successione minima di mosse necessarie.
Una ripartizione primitiva di una coppia (a,b ) è fornita dai seguenti due teoremi:

Teorema 1. 
La coppia (a,b ), se $\displaystyle a=b\neq 2$, oppure $\displaystyle a\neq b$ e il maggiore tra a e b non supera il doppio dell’altro, ammette una determinabile ripartizione primitiva di classe t + r ove t è il quoziente ed r il resto della divisione a + b per 3.

Teorema 2.
La coppia (a,b), se è $\displaystyle a\neq b$ ed il maggiore tra a e b, distinto da 1, supera il doppio dell’altro, ammette una determinabile ripartizione primitiva di classe (z + v)/2, ove z è l’elemento maggiore della coppia e v il resto della divisione della differenza tra tale elemento e il doppio dell’altro per 4.

Nota.- Il problema è stato risolto con un lavoro del matematico Gentile, e di cui ho ricevuto una copia per gentile concessione di un suo nipote.