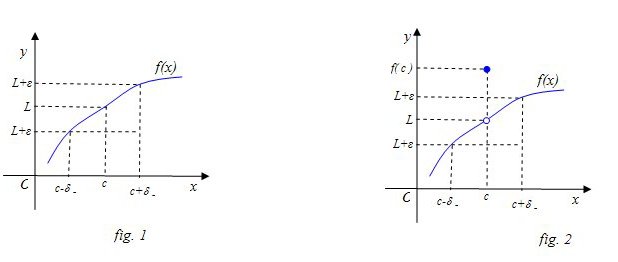Sia y = f(x) una funzione reale definita in un sottoinsieme X di R e c un punto d’accumulazione per l’insieme X.
Definizione.- Limite di f(x) per x che tende a c.
Si dice che f(x) tende al numero reale L per x che tende a c, o che f(x) ha per limite L in c, e si scrive:
\[\lim_{x\rightarrow c}f(x)=L\]
se è verificata la seguente proprietà:
\[1)\, \, \, \forall J\, di\, L\, \exists\, I_{J}\, di\, c\, :\, \forall x\in \left (( I_{J}-\left \{ c \right \})\cap X \right )\, \, f(x)\in J\]
J è un intorno di L e I di c
OSSERVAZIONE
L’intorno I di c dipende dall’intorno J e pertanto è corretto indicarlo, ossia conviene scrivere in luogo di
.
L’intorno I non è univocamente determinato dall’intorno J, e l’ampiezza di I dipende dall’ampiezza di J.
Inoltre, notiamo che il punto c può appartenere ad X, essendo di accumulazione per X, e quindi l’intorno I è da intendersi come un intorno bucato di c, ossia la nozione di limite è un concetto che riguarda il comportamento della funzione in un intorno di I di c, ma non nel punto c.
La (1) si può esprimere equivalentemente nel seguente modo:
oppure
con
non appena si ricordi che un intorno I di c contiene un intervallo aperto contenente c e che la condizione f(x) Î J equivale a
,
ove e è il generico raggio dell’intorno di centro L.
La proprietà (1) e quindi la (2), esprime geometricamente, in un riferimento Oxy del piano, il fatto
che i punti del grafico della funzione f(x) aventi ascissa , distinti da c, sono compresi nel rettangolo di dimensioni
.
Nelle figure 1 e 2 sono illustrate alcune eventualità.
Esempio 1.- Verifica di un limite … clicca qui