I numeri complessi.-
I numeri complessi.-
“Assolutamente fondamentali per la struttura della meccanica quantistica, i numeri complessi sono perciò basilari per il funzionamento del mondo stesso in cui viviamo. Essi costituiscono anche uno dei grandi miracoli della matematica.” R. Penrose
Ogni numero complesso z può essere scritto in forma algebrica nel seguente modo:\[z=a+ib\]ove a e b sono numeri reali e i, l’unità immaginaria, tale che: \[i^{2}=-1\]ossia: \[i=\sqrt{-1}\]
Il numero reale a è la parte reale del numero complesso z, mentre il numero reale b è la parte reale dell’immaginario. L’insieme di tutti i numeri complessi si indica con la lettera C, e dato che per b = 0 il numero complesso \[z=a+ib\] si riduce a z = a (dunque è un numero reale), include R, \[R\subseteq C\] l’insieme dei numeri reali. Se a = 0 e b è diverso da zero si ottiene un numero immaginario puro z = bi. Ricordiamo che le potenze dell’unità immaginaria i sono cicliche e sono sempre uguali ai seguenti 4 valori:
\[ i^{0}=1,\,\,i^{1}=i,\,\,i^{2}=-1,\,\,i^{3}=-i\]
Due numeri complessi \[z=a+ib,\, \, \, \, \, w=c+id\]sono uguali se e solo se a = c e b = d.
Non ha senso invece confrontare due numeri complessi onde stabilire chi è il più grande e il più piccolo, perché l’insieme C non è ordinato.
I numeri complessi si possono rappresentare nel piano di Argand Gauss.
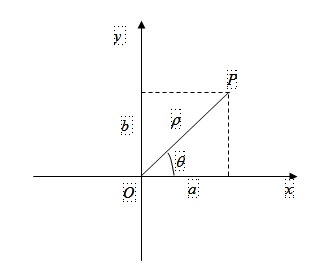
Il piano di Argand Gauss è il piano , in cui è stato fissato un riferimento cartesiano Oxy, e ogni punto P, di coordinate (a, b), del piano viene associato con il numero numero complesso\[z=a+ib\]e viceversa.
La parte reale a si prende sull’asse x (detto asse reale) e la parte immaginaria b sull’asse y (detto asse immaginario); P(a,b) si dice immagine di z e si scrive P(z), mentre z si dice l’affissa di P.
Il punto P si può rappresentare anche in funzione delle coordinate polari \[\rho\, \, e\, \, \, \theta\]
In tal caso sussistono tra le coordinate cartesiane (a, b) e le polari \[\rho\, \, e\, \, \, \theta\]
le seguenti relazioni: \[a=\rho cos\theta ,\, \, \, b=\rho sen\theta\] con il valore principale dell’anomalia \[\theta \in [0,2\pi )\] mentre per l’argomento si ha\[\rho =\sqrt{a^{2}+b^{2}}\]Un numero complesso \[z=a+ib\] si può scrivere anche in altre forme:
Forma trigonometrica \[z=\rho \left ( cos\theta +isen\theta \right )\]Forma esponenziale \[z=\rho \cdot e^{i\theta }\] ove \[e^{i\cdot \theta }=cos\theta +isen\theta,\, \, \, \forall \theta \in R\] è la formula di Eulero. Per \[\theta =\pi \] si ottiene l’identità di Eulero: \[e^{i\pi }=-1\to e^{i\pi }+1=0\]