Problema 1.- Sia ABC un triangolo equilatero di lato a, sul prolungamento di AB si prenda un punto P, sia poi K la proiezione di P su lalo AC. Posto PB = x calcolare il seguente limite \[\lim_{x\rightarrow +\infty }\left ( \frac{2\sqrt{3}}{3}\cdot \overline{PK}-\overline{PC} \right )\]
Risoluzione
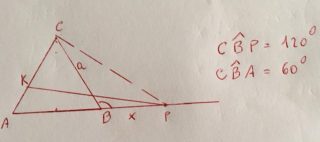
Nel triangolo BCP, applicando il teorema di Carnot, si ha:
\[\overline{CP}=\sqrt{\overline{BP}\, ^{2}+\overline{CB}\, ^{2}-2\overline{PB}\cdot \overline{CB}\cdot cos120^{\circ}}=\sqrt{x^{2}+a^{2}-2ax\left ( -\frac{1}{2} \right )}=\sqrt{x^{2}+a^{2}+ax}\]
Nel triangolo rettangolo KPA, rettangolo in K, applicando il teorema sui triangoli rettangoli si ha:
\[\overline{PK}=\overline{AP}sen\left ( 60^{\circ} \right )=(a+x)\frac{\sqrt{3}}{2}\]
essendo \[\overline{AP}=a+x\]
Pertanto il limite da calcolare è il seguente \[\lim_{x\rightarrow +\infty }\left [ \frac{2\sqrt{3}}{3}\left ( a+x \right )\frac{\sqrt{3}}{2}-\sqrt{x^{2}+a^{2}+ax} \right ]=\lim_{x\rightarrow +\infty}\left ( a+x-\sqrt{x^{2}+a^{2}+ax} \right )\]
e vale \[\frac{a}{2}\]
Il limite dato si può calcolare razionalizzando il numeratore e poi mettendo in evidenza x al denominatore.
Problema 2.- Data una semicerconferenza di diametro AC e centro O, tracciare la semiretta uscente da A, perpendicolare ad AC e giacente rispetto ad AC dalla stessa parte della circonferenza. Detto M un punt generico su tale semiretta, indicare con x la distanza di M da A. Da M staccare l’ulteriore tangente in B alla semicirconferenza. Detta K l’intersezione della semicirconferenza con il segmento OM, determinare l’area del quadrilatero ACBK in funzione di x. Calcolare il valore di y per x tendente a + infinito.
1° Quesito Sessione Ordinaria 1990
Risoluzione
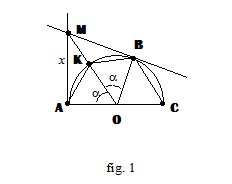
Per il teorema delle tangenti ad una circonferenza si ha che la retta OM è bisettrice dell’angolo AOB (fig. 1). Pertanto si ha: \[A\hat{O}M=B\hat{O}M,\, \, B\hat{O}C=\pi -2\alpha\]


——–
2) Vedi area di un triangolo qualsiasi
3) Abbiamo applicato le relazioni tra triangoli rettangoli al triangolo AMO
Problema N.3.- Dato un trapezio ABCD rettangolo in A, di lato obliquo CB, sia AB = CB = 10a, DA = 8a e area $\displaystyle 56a^{2}$. Tracciamo la parallela alla diagonale AC e sia M il punto d’intersezione con il lato CB ed N il punto d’intersezione con il lato AB. Posto MB = x calcolare il seguente limite \[\lim_{x\rightarrow 0}\frac{\overline{MN}-\overline{MB}}{\overline{MH}}\] ove H è la proiezione del punto M su AB.
Risoluzione
La base minore del trapezio si può calcolare con la formula inversa dell’area e vale 4a. Di conseguenza la diagonale AC si può calcolare con il teorema di Pitagora e vale \[\overline{AC}=\sqrt{\overline{DA}^{2}+\overline{DC}^{2}}=\sqrt{16a^{2}+64a^{2}}=5a\]
I triangoli ABC e NBM sono simili per il corollario del teorema di Talete essendo MN parallela ad AC, dunque si ha la seguente proporzione:
\[CB:BM=AC:MN\]
ossia
\[\overline{MN}=\frac{x\cdot 4a\sqrt{5}}{10a}=\frac{2}{5}x\sqrt{5}\]
mentre MH si può calcolare ragionando nei triangoli ACB e NMB e si ha:
\[\overline{MH}=\frac{\overline{CH}\cdot \overline{NB}}{\overline{AB}}=\frac{4x}{5}\]
Pertanto il limite da calcolare vale: \[\lim_{x\rightarrow 0}\frac{\frac{2\cdot x\sqrt{5}}{5}-x}{\frac{4x}{5}}=\frac{2\sqrt{2}-5}{4}\]
Problema 5.- In una circonferenza di raggio r si consideri la corda AB che dista r/2 dal centro O della circonferenza. Si prenda sul maggiore degli archi AB il punto C, si prolunghi AC di un segmento CD tale che CD = AC e si determini per quale posizione di C è massima l’area del triangolo CDB.
Sessione suppletiva 1981, primo quesito.
Svolgimento
Ragioniamo nel triangolo rettangolo BOH (fig. 6). Applicando il teorema di Pitagora si ha:
\[\overline{BH}=\sqrt{\overline{BO}^{2}-\overline{OH}^{2}}=\sqrt{r^{2}-\left ( \frac{r}{2} \right )^{2}}=\frac{r}{2}\sqrt{3}\]
e poi \[\overline{BA}=2\cdot \overline{BH}=r\sqrt{3}\]
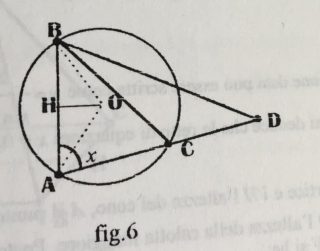
Inoltre si ha:\[H\hat{B}O=H\hat{A}O=30^{\circ}\] mentre l’angolo al centro \[B\hat{O}A=120^{\circ}\] e l’angolo alla circonferenza \[B\hat{C}A=\frac{1}{2}\cdot B\hat{O}A=60^{\circ}\] Ne consegue che l’angolo \[B\hat{C}D=180^{\circ}-60^{\circ}=120^{\circ}\]
Indicato poi con x l’angolo $B\hat{A}C=x$ si ha che $A\hat{B}C=120^{\circ}-x$, con\[0^{\circ}<x<120^{\circ}\] tenendo conto che la tangente in A è perpendicolare al raggio AO.
Applicando il teorema dei seni al triangolo ABC si ha \[\overline{AC}=2rsen\left ( 120^{\circ}-x \right ), \, \, \, \, \overline{BC}=2rsen\, x\]
Pertanto l’area del triangolo BCD è: \[A=\frac{1}{2}\cdot \overline{CD}\cdot \overline{BC}\cdot sen(B\hat{C}D)\] e sostituendo le quantità determinate si ha: \[A(x)=\frac{1}{2}\cdot 2rsenx\cdot 2rsen\left ( 120^{\circ}-x \right )sen(120^{\circ})=2r^{2}senx\cdot sen(120-x)\cdot sen(120)=\frac{\sqrt{3}}{2}r^{2}senx\left ( \sqrt{3}cosx+senx \right )\]
e la funzione da massimizzare è: \[A(x)=senx\left ( \sqrt{3}cosx+senx \right )\] avendo trascuratato la costante moltiplicativa $\frac{\sqrt{3}}{2}r^{2}$. La derivata prima della funzione A(x) è\[A'(x)=cosx\left ( \sqrt{3}cosx+senx \right )+senx\left ( -\sqrt{3}cosx+senx \right )=\sqrt{3}\left ( cos^{2}x-sen^{2}x \right )+2senxcosx=\sqrt{3}cos2x+sen2x\] e dunque da \[A'(x)\geqslant 0\Rightarrow \sqrt{3}cos2x+sen2x\geqslant 0\] si ottiene che l’area è massima per \[x=60^{\circ}\]
