Proponiamo il seguente quiz (vedi foto sinistra), a detta di alcuni intuitivo e non correlato a schemi logici matematici. Può essere, ma…
Nel quiz in sostanza si chiede di stabilire il valore numerico da mettere al posto del punto interrogativo nella quarta riga. Alcuni ritengono che tale numero sia unico, io qui sosterrò che non è così. Pertanto chiederò qui di risolvere il problema cioè di trovare una soluzione, se ammette soluzione, e se ne ammette di trovare quella più semplice.
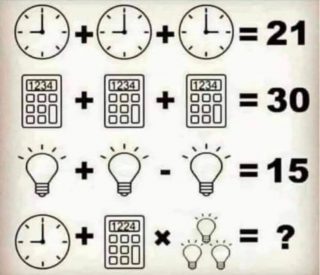
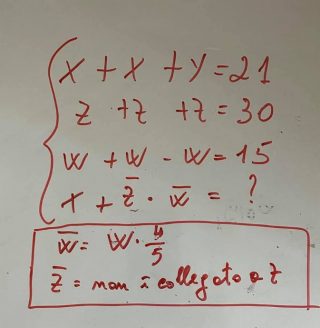
Se si utilizzano delle incognite letterali il problema diventa quello della seconda foto e si evidenzia che z e $\displaystyle \overline{z}$ ( segnato) non sono “collegate” da alcuna regola precisa ma da interpretazione personale in base ai simboli grafici utilizzati. E tali simboli sono utilizzati a piacere, a dir poco…
Pertanto il problema dovrebbe essere indeterminato, potendo ogni persona interpretarli a piacere.
Alcuni però propongono come soluzione della quarta riga il valore 333, affermando che sia quella più semplice e intuitiva, ma non vi è ragione o regola per avallare tale affermazione rispetto ad un’altra ipotetica soluzione. Anzi, quello che può essere semplice o intuitivo per una persona non è detto che lo sia per un’altra.
Chi sostiene che tale soluzione sia la più semplice e intuitiva dice anche che il problema è un quiz intuitivo e non di logica e matematica. Ma non è così, come cercherò di far capire nel prosieguo.
Molti escludono i valori numerici fratti (così come i valori negativi o lo zero) per i singoli oggetti, ma non sta scritto da nessuna parte che la calcolatrice indicata dal 1224 non possa avere valore numerico corrispondente pari a 20/3 (o a zero) con risultato poi finale della quarta riga pari a 249 e non 333.
Sembra più semplice fare i calcoli con numeri interi, ma nella terza riga il calcolo corretto si fa con una proporzione, dunque frazione. Inoltre nella seconda riga per ipotizzare la somma delle cifre 1 + 2 + 3 + 4 = 10 come regola, bisogna passare ad una operazione di addizione non usuale e che è diversa da quella usuale della prima riga (somma semplice dei valori indicati) e che nella terza diventa tutt’altra regola, cioè una proporzione appunto Dalla prima riga si potrebbe evincere che nella seconda riga ci sia da fare un’addizione dei numeri indicati ossia 1234 + 1234 + 1234, ma non darebbe 30, e dunque bisogna passare ad altra tipologia di addizione: per esempio si potrebbero sommare proprio le cifre del numero 1234 come detto sopra o magari considerare le calcolatrici come identiche indicarle con una lettera z e calcolare il suo valore risolvendo l’equazione $\displaystyle 3z=30$, e ottenere sempre 10, ma come escludere una regola/procedura rispetto all’altra? E non ci possono essere altre procedure più semplici o intuitive? In pratica sappiamo che nella prima riga vi è indicata un’addizione ordinaria (usuale), nella seconda dobbiamo ipotizzare noi una nuova tipologia di operazione o procedura e nella terza vi è una proporzione. Infine dobbiamo correlare i dati espressi nelle prime tre righe (e la seconda presenta almeno due possibilità) con la quarta riga stabilendo una connessione tra la prima calcolatrice 1234 con la seconda, quella con il 1224.
Non potendo scegliere tra le due procedure adottate nella seconda riga perché entrambe valide il problema è indeterminato. Ma si potrebbe obiettare che i simboli grafici adottati diano ulteriori informazioni e che dovendoci essere una soluzione si possa arguire che la 333 sia la soluzione, individuata dalla procedura di sommare nella seconda riga le cifre del numero 1234 per tre volte. Ma se nella seconda riga consideriamo la calcolatrice come l’incognita z e quella della quarta riga con $\displaystyle \overline{z}$, la differenza delle decine, tre nella prima e due nella seconda, ci può far ipotizzare che il valore della calcolatrice $\displaystyle \overline{z}$ sia collegato al numero delle sue decine rispetto a quelle di z. Pertanto si potrebbe pensare alla proporzione: 10 sta a 3 come $\displaystyle x$ sta a 2, $\displaystyle 10 : 3 = x : 2$, e ottenere x = 20/3, dopodiché ottenere valore finale nella quarta riga 249. Come escludere quest’altra possibilità? E per la verità vi sono molti altri modi di correlare le due calcolatrici, ad esempio un altro è quello di correlarle alle unità della calcolatrice, 1234 unità e 1224 dell’altra, e non sono esclusi altri modi di correlarle. Il punto è proprio come correlare le due calcolatrici in base ai dati del problema (le prime tre righe); e qui entra in gioco il gusto personale e la personale conoscenza di più cose. La soluzione 333 è una soluzione amata da tanti perché è la prima tra quelle che vengono in mente, diciamo intuitiva… ma non è l’unica, non potendo escludere tutte le altre in base ai dati forniti nelle tre righe superiori, non è accettabile come la soluzione, ma solo come una soluzione. Quindi il problema è di fatto indeterminato avendo più soluzioni. Anzi la soluzione 333 a me sembra più complicata da ottenere rispetto ad altre, visto che bisogna ipotizzare una nuova regola di addizione.
E per escludere, poi, tutte le altre soluzioni a favore di una ben precisa soluzione si necessita di una vera dimostrazione, il che farebbe diventare il quiz tutt’altro che intuitivo, ma proprio di tipo logico e matematico, dovendo fare una vera e propria dimostrazione del perché le altre procedure o soluzioni non siano corrette, ammesso e non concesso che la nozione di semplicità sia la stessa per tutti. Naturalmente, se il problema chiedesse di determinare una soluzione allora il discorso cambierebbe… la prima soluzione trovata è quella giusta purché soddisfi a tutte le condizioni date. Ammettendo che la soluzione sia unica e che sia definito un procedimento per stabilire quella più semplice allora la soluzione da noi scelta potrebbe essere, o non essere, la più semplice, ma visto che non è definita la nozione di semplicità e potendo essere a piacere, non ha senso parlare di soluzione del problema avvalorando la soluzione trovata con una presunta sua semplicità. Il problema dunque ammette più soluzioni e non potendo sapere cosa si intenda per “semplicità”, bisogna convenire che di fatto il problema o è indeterminato o più complicato di quello che si voglia far credere.
In definitiva, il quiz è da considerarsi o non intuitivo o indeterminato… il che non significa che non possa piacere la soluzione 333, è una delle possibili soluzioni.
Sono sicuro che però ancora non si è convinti… allora provate a rispondere a quest’altro quiz:
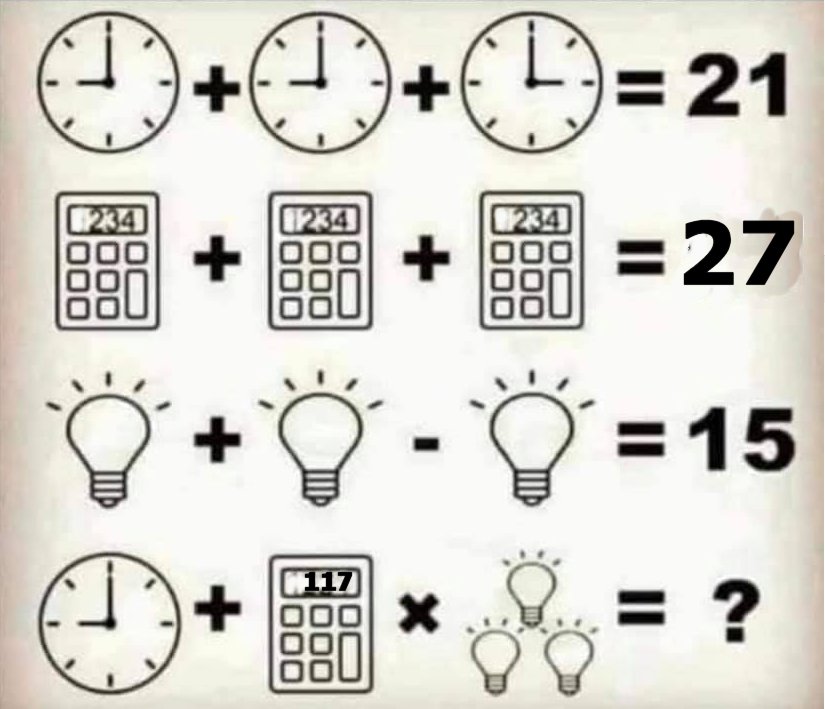
….ehehhehehe… qual è la risposta più semplice? Quella che piace a me o quella che piace a voi?
E ancora, provate a rispondere a quest’altro:
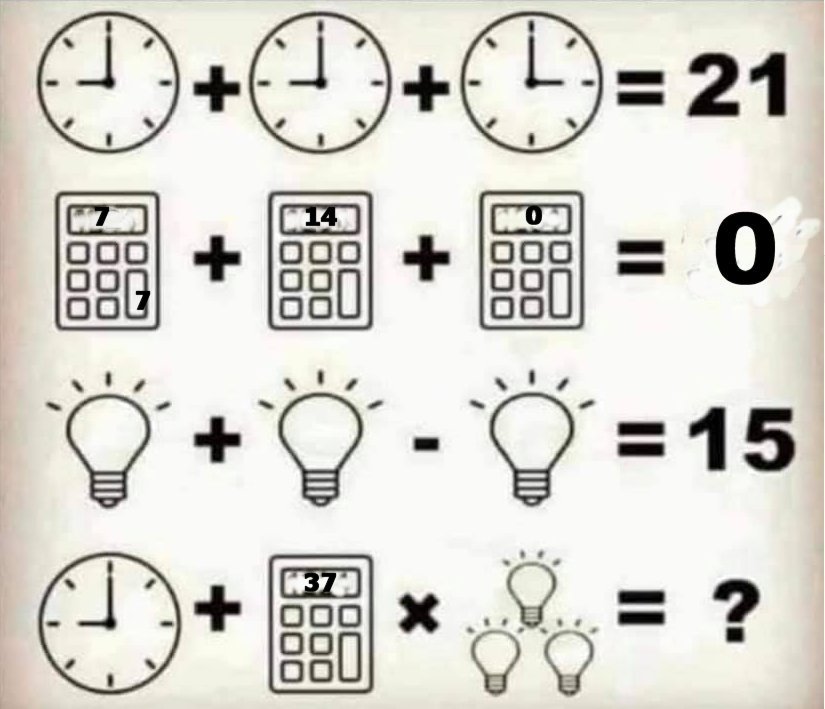
OSSERVAZIONE: Da un punto di vista matematico il quiz riportato nella prima figura (e nelle altre) è totalmente sconclusionato, nonostante la mente umana riesca a trovare una soluzione apparente, o le tante altre soluzioni. L’errore più grosso è quello delle operazioni fatte o indicate nei dati del problema e poi immaginate a piacere nel rigo della risposta al problema. Nella prima riga vi è un’operazione matematica usuale, tradotta in simboli ma riconducibile alla ordinaria operazione di addizione che si conosce dalle scuole elementari. Nella seconda riga invece vi è il simbolo di addizione (+), ma l’operazione è da interpretare a piacere. E l’operazione ritenuta da alcuni la più semplice, ovvero il sommare le cifre del numero 1234 non è più la stessa operazione del rigo precedente pur indicandola con lo stesso simbolo +. A rigore si tratta di un’altra operazione e dovrebbe essere indicata con un altro simbolo; l’indicazione del segno + tra le calcolatrici uguali non implica che trattasi di nuova operazione e di quale tipo essa sia. Nella terza riga si fa uso anche della sottrazione, ma si ritorna al significato usuale di addizione e sottrazione. Nella quarta riga, quella della risposta, cambia nuovamente tutto. Si richiede che si faccia un’operazione di addizione usuale, poi di associare alla calcolatrice un numero con un’operazione non ordinaria (la somma delle cifre) e infine di moltiplicare il numero corrispondente alla calcolatrice tramite una moltiplicazione ordinaria. Penso ce ne sia abbastanza per dire che la mente umana faccia miracoli a trovare una delle tante soluzioni, ma la matematica è un’altra cosa. (Si rimanda al concetto di operazione interna ed esterna tra due insiemi).
Vedi anche Definizione di Gruppo
Nell’ultima figura abbiamo utilizzato la congruenza modulo 7 nella seconda riga, la qual cosa trasforma la seconda riga nell’evidente uguaglianza $\displaystyle 0+0+0=0$ e di conseguenza suggerisce che la calcolatrice della quarta riga abbia valore corrispondente al 37 nella congruenza modulo 7, ovvero \[37\equiv 2\, \, \left ( mod.7 \right )\]
In definitiva la calcolatrice della quarta riga vale 2 e il risultato finale è 81.
