 Ramanujan Srinivasa Aaiyangar è stato uno dei più grandi matematici di tutti i tempi, al pari di Gauss o di Eulero, nonchè un prodigio nelle capacità di calcolo: una specie di Mozart della matematica. Dotato di un talento straordinario per la teoria dei numeri, ha lasciato taccuini (Notebooks di Ramanujan) pieni di formule. Ancora oggi ci si chiede come abbia potuto scoprirle senza poterne dare delle vere dimostrazioni.
Ramanujan Srinivasa Aaiyangar è stato uno dei più grandi matematici di tutti i tempi, al pari di Gauss o di Eulero, nonchè un prodigio nelle capacità di calcolo: una specie di Mozart della matematica. Dotato di un talento straordinario per la teoria dei numeri, ha lasciato taccuini (Notebooks di Ramanujan) pieni di formule. Ancora oggi ci si chiede come abbia potuto scoprirle senza poterne dare delle vere dimostrazioni.
Si racconta che il grande matematico inglese Hardy, dicesse a Ramanujan malato di tubercolosi nell’ospedale di Putney:
“Il numero del mio taxi è il 1729, mi sembra un numero alquanto stupido”. Al che Ramanujan rispose: “No Hardy! No! E’ un numero molto interessante. Il più piccolo esprimibile come somma di due cubi in due diversi modi:
\[1729=10^{3}+9^{3},\, \, 1729=12^{3}+1^{3}\]
Ramanujan nacque a Kumbakonam presso Madras nel 1887, non in un grande centro intellettuale, purtroppo, ma proprio nella parte sbagliata del mondo, da una famiglia poverissima anche se di casta elevata. Fin dalla più tenera età, Ramanujan, si era appassionato ai numeri e alla matematica e aveva letto ogni libro che gli venisse a tiro. Poverissimo e con una moglie da mantenere accetta di lavorare come impiegato al porto di Madras, con uno stipendio di 20 sterline annue.
Nel gennaio 1913 viene scoperto dal grande matematico inglese G.H. Hardy, docente di matematica a Cambridge, vincitore di diversi premi e il più illustre matematico inglese.
Hardy intuì immediatamente il genio matematico del povero indiano e si offrì di aiutarlo in tutti i modi possibili. Per liberarlo dai problemi economici e per permettergli di continuare gli studi lo fece venire a Cambridge, ove all’età di 30 anni fu eletto Fellow della Royal Society.
Morirà, purtroppo, all’età di 33 anni, nel 1918 malato di tubercolosi, tra le braccia della moglie.
Hardy, per ricordare il genio di Ramanujan, scriverà:
“Quando sono depresso e costretto ad ascoltare gente pomposa e noiosa, mi dico: “Be’, io ho fatto una cosa che Voi non avreste mai potuto fare e cioè aver collaborato con Ramanujan pressappoco alla pari”.
Qui di seguito riporto alcune sensazionali formule scoperte da Ramanujan:
\[1+2+3+4+5…=-\frac{1}{12}\]
\[\frac{2}{\pi }=1-5\left ( \frac{1}{2} \right )^{3}+9\left ( \frac{1}{2}\cdot \frac{3}{4} \right )^{3}-13\left ( \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6} \right )^{3}+…\]
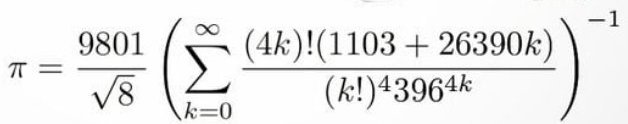
Hardy: Il genio di Ramanujan invece è selvaggio e incoerente, come una pianta di rose rampicanti che avrebbe dovuto essere preparata per crescere su un graticcio, e invece sfugge al controllo.
