1° CASO.- Il punto P appartiene alla circonferenza (o altra curva di secondo grado)
Se il punto P(x1 ; y1) appartiene alla circonferenza d’equazione
$\displaystyle x^{2}+y^{2}+ax+by+c=0$
( fig. 1), la retta tangente t alla circonferenza passante per P, è unica. Per determinare l’equazione della retta t tangente alla circonferenza nel punto P si può applicare la seguente formula di sdoppiamento: \[xx_{1}+yy_{1}+\frac{a}{2}\left ( x+x_{1} \right )+\frac{b}{2}\left (y+y_{1} \right )+c=0\]
Se al posto della circonferenza consideriamo la parabola, l’ellisse o l’iperbole l’equazione della tangente in P è rispettivamente:
\[\left (\frac{y+y_{1}}{2} \right )=axx_{1}+b\frac{x+x_{1}}{2}+c\]
per la parabola con asse parallelo all’asse y e di equazione $\displaystyle y=ax^{2}+bx+c$ ;
\[\left (\frac{x+x_{1}}{2} \right )=ayy_{1}+b\frac{y+y_{1}}{2}+c\]
per la parabola con asse parallelo all’asse x d’equazione $\displaystyle x=ay^{2}+by+c$ ;
\[\frac{xx_{1}}{a^{2}}+\frac{yy_{1}}{b^{2}}=1\]
per l’ellisse canonica d’equazione $\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ ;
\[\frac{xx_{1}}{a^{2}}-\frac{yy_{1}}{b^{2}}=1\]
per l’iperbole canonica d’equazione $\displaystyle \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ ..
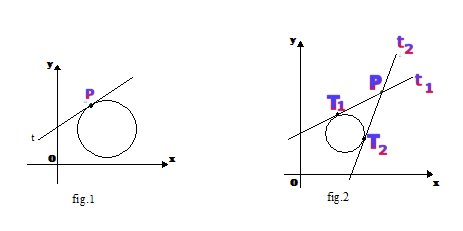
2° CASO.- Il punto P è esterno alla circonferenza (o ad altra curva di secondo grado)
Se il punto P(x1 ; y1) è esterno ( fig. 2) alla circonferenza d’equazione $\displaystyle x^{2}+y^{2}+ax+by+c=0$ le rette tangenti alla curva e condotte per P sono due.
Per determinare le due rette tangenti si procede nel seguente modo:
- Si considera l’equazione del fascio di rette di centro P:\[y-y_{1}=m\left ( x-x_{1} \right )\]
- si determina m imponendo la condizione di tangenza \[\Delta =0\]
nell’equazione di 2° grado in x ( o in y) che scaturisce dal sistema formato dall’equazione \[y-y_{1}=m\left ( x-x_{1} \right )\] e dall’equazione della circonferenza\[x^{2}+y^{2}+ax+by+c=0\] . - Risolta l’equazione \[\Delta =0\] nell’incognita m si ottengono i due coefficienti angolari $\displaystyle m_{1},\, \, \, m_{2}$ delle due rette tangenti.
Pertanto le tangenti alla circonferenza (in generale alla curva f(x,y) = 0), condotte per P, hanno equazioni:
\[t_{1})\,\, \, y-y_{1}=m_{1}(x-x_{1})\]
\[t_{2})\,\, \, y-y_{1}=m_{2}(x-x_{1})\]
Notiamo che il metodo esposto nel secondo caso si può applicare anche quando il punto P appartiene alla circonferenza.
Analogamente si procede se al posto della circonferenza si considera una parabola, un’ellisse o un’iperbole.
Ricordiamo che se il punto P è interno alla curva allora le rette tangenti non esistono.
Per determinare i punti di tangenza, ovvero i punti in cui le tangenti toccano la circonferenza (la curva) bisogna risolvere il sistema formato dall’equazione della curva e dalla tangente in quel punto.
Esempio 1.- Determinare l’equazione della tangente alla circonferenza \[x^{2}+y^{2}+4x+2y+1=0\] passante per il punto O(0,0).
Se non sai risolvere il problema prova a vedere qualche mio video su Youtube
Esempio 2.- Determinare le rette tangenti alla circonferenza \[x^{2}+y^{2}+2x-4=0\]
condotte per il punto P(6,1)
Risoluzione
Dobbiamo considerare il sistema \[\left\{\begin{matrix} y-1 &=m(x-6) \\ x^{2}+y^{2}+2x-4 &=0 \end{matrix}\right.\] e di conseguenza l’equazione di secondo grado
\[x^{2}+(mx-6m+1)^{2}+2x-4=0\Rightarrow x^{2}\left ( 1+m^{2} \right )+2x\left ( 1+m-6m^{2} \right )+36m^{2}-12m-3=0\]
nella quale imponendo la condizione di tangenza si ottiene l’equazione in m:
\[\left ( 1+m-6m^{2} \right )^{2}-\left ( 1+m^{2} \right )\left ( 36m^{2}-12m-3 \right )=0\]
ossia \[22m^{2}-7m-2=0\]
risolta la quale si ottengono i due valori di m relativi alle due tangenti: m = 1/2, m = -2/11.
Dunque le due rette tangenti sono… (dai che ci riesci da solo…)
Esempio 3.- Determinare le rette tangenti alla parabola \[y=x^{2}-2x+1\] condotte per il punto P (0,-1)
Esempio 4.- Determinare le rette tangenti alla parabola \[y=x^{2}-5x+1\] condotte per il punto P (3,-6)
