In questa pagina puoi prendere visione di alcuni tipici problemi assegnati alla prova scritta della Maturità Scientifica. Se non riesci a risolverli puoi provare a seguire i miei video gratuiti sul canale Youtube: Matematica Facile
Problema 1.- Determinare i coefficienti della curva di equazione \[y=ax^{4}+bx^{3}+cx^{2}+dx+e\] sapendo che:
- si annulla per x = 0;
- la derivata prima si annulla per x = 0, x = 1, x =2;
- nel punto di ascissa x = -1 la tangente alla curva è parallela alla retta y = -x.
In base alle condizioni assegnate i coefficienti a, b, c, d, e si determinano risolvendo il sistema \[\left\{\begin{matrix} e &=0 \\ d &=0 \\ 4a+3b+2c+d &=0 \\ 32a+12b+4c+d &=0 \\ -4a+3b-2c+d &=-1 \end{matrix}\right.\] e si ha \[a=\frac{1}{24},\, \, b =-\frac{1}{6},\, \, c=\frac{1}{6},\, \, d = 0,\, \, e =0\]
Quindi l’equazione della curva è \[y=\frac{1}{24}x^{4}-\frac{1}{6}x^{3}+\frac{1}{6}x^{2}\]
Problema 2.- Determinare i coefficienti della curva di equazione \[y=ax^{3}+bx^{2}+cx+d\] sapendo che la curva grafico tocca la retta y = x nel punto A(1,1) e la retta y = 0 nel punto B(3,0). Si disegni il grafico della funzione
Sessione ordinaria 1982 – Esercizio risolto qui
Problema 3.- Determinare i coefficienti della curva di equazione \[y=\frac{ax^{3}+bx^{2}+cx+d}{x^{2}}\] sapendo che la curva da essa rappresentata ammetta un asintoto obliquo di equazione y = x-2 e che abbia un estremo relativo nel punto di ascissa x = 2 e un flesso nel punto di ascissa x = -1. Se ne disegni il grafico
Sessione suppletiva 1981 – Esercizio n 10 pag. 144 proposto con suggerimenti e soluzioni qui
Problema 4.- Determinare i coefficienti della curva di equazione \[f(x)=\frac{a}{x}+\frac{b}{x+1}+\frac{c}{x+2}\] in modo che f(1) = 1/6, f(2) = 1/24, f(1/2) = 8/15 e si disegni iil grafico della funzione così ottenuta.
Sessione suppletiva 1974
Problema 5.- Determinare i coefficienti della curva di equazione\[y=ax^{3}+bx^{2}+cx+d\] in modo che la curva da essa rappresentata abbia due estremi relativi in P(1, 1) e Q(-1, -1). Se ne disegni il grafico
Sessione suppletiva 1983
Problema 6.- Determinare i coefficienti della curva di equazione
\[y=a^{2}x^{3}-3a(2a-3)x^{2}+9(a-1)(a-3)x+b\]
in modo che il punto di minimo e il punto di massimo abbiano rispettivamente ordinate 0 e 1.
Estratto dalla Sessione suppletiva 1990 –
Problema 7.- Determinare i coefficienti della curva di equazione\[y=1+ax+\frac{b}{x^{2}}\] in modo che la curva da essa rappresentata abbia un minimo relativo nel punto P(1,0) Se ne disegni il grafico
Estratto dalla Sessione suppletiva 1978
Problema 8.- Determinare i coefficienti della curva di equazione\[y=senx+a\cdot cosx+b\, \, \, \, \, in\, \left [ -\pi ,\pi \right ]\] in modo che la curva da essa rappresentata abbia un massimo relativo \[y=0 \, \, \, \, in\, \, \, \,x=\frac{\pi }{6}\]
Se ne disegni il grafico.
Estratto dalla Sessione suppletiva 1978
Problema 9.- Determinare i coefficienti della curva di equazione\[y=asenx+bcosx\]
in modo che la curva da essa rappresentata verifichi la condizione \[y=1 \, \, \, \, \, \, \,x=\frac{2\pi }{3}\] e che i valori estremanti siano -2 e 2
Se ne disegni il grafico in [0, 2pi].
Estratto dalla Sessione ordinaria 1977
Problema 10.- Sono assegnate le funzioni in x: \[\frac{x^{4}+ax^{2}+b}{x^{2}+1}\], dove a e b sono parametri reali. Fra tali funzioni indicare con f(x) quella per cui la curva k d’equazione y = f(x) soddisfi alle seguenti due condizioni: la retta d’equazione y = 1 sechi k in due punti e sia tangente ad essa in un punto; l’asse x sia tangente a k in due punti distinti.
Estratto dalla Sessione ordinaria 1997
Se non sai svolgere i problemi indicati prova a seguire alcuni video corsi gratuiti. Clicca qui
Problema 11.- E’ assegnata la funzione \[f(x)=\frac{2x+1}{x^{2}+mx+\left | m \right |}\]
- determinare il suo dominio di derivabilità
- calcolare per quale valore di m la funzione ammette derivata nulla in x = 1
- Studiare la funzione f(x) corrispondente al valore di m così trovato e disegnare il grafico in uno piano Oxy
- calcolare l’area della regione finita di piano delimitata dalla curva grafico dall’asse x e dalla retta x = 1
Estratto Sessione ordinaria 2003
Problema 12.- Si considerino le funzion f e g determinate da \[f(x)=logx,\: \: \: \: g(x)ax^{2}\] essendo a un parametro reale e il logaritmo in base il numero di Nepero e.
Si discuta al variare di a l’equazione \[log\, x=ax^{2}\] e si dica per quale valore i grafici di f e g sono tra loro tangenti. Posto a = 1 si calcoli l’area della parte di piano delimitata dai grafici di f e g e dalle rette x = 1 e x = 2. Si studi la funzione \[h(x)=log\, x-ax^{2}\] scegliendo per a un valore maggiore di 1/2e e se ne disegni il grafico
Sessione ordinaria 2006
Problema 13.- Data la funzione così definita \[f(x)=-x^{3}+kx+9\] con k intero…
Sessione ordinaria 2018
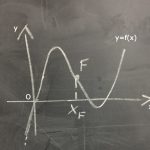
Problema 14.- Assegnato un numero reale positivo k, considerare le funzioni f e g così definite \[f(x)=\sqrt{x}\left ( k-x \right ),\, \, g(x)=x^{2}\left ( x-k \right )\]
- Provare che qualunque sia k, nell’intervallo [0, k], il grafico di f ha un unico punto di massimo F(xF, yF) e il grafico di g ha un unico punto di minimo G(xG, yG). Verificare che \[x_{G}=2x_{F}\, \, e\, \, y_{G}=-\left ( y_{F} \right )^{2}\]
- verificare che qualunque sia k >0 i grafici delle funzioni sono ortogonali nell’origine. Determinare per quale valore di k i grafici delle due funzioni si intersecano ortogonalmente nel loro ulteriore punto comune.
Simulazione 2019, estratto del problema 2.
Problema 15.- Data la funzione esponenziale $y=2^{\frac{ax+b}{x+c}}$ determinare i parametri a, b, c in modo che il grafico della funzione passi per il punto A(-4,2), abbia un asintoto orizzontale d’quazione y = 8 e la funzione sia definita in R – [6}. Vedi il video
Problemi con studio di funzioni senza parametri. Alla Maturità Scientifica sono state assegnate le seguenti funzioni da studiare e disegnarne il grafico. Il lettore può così prendere visione di alcune tipologie di funzioni assegnate. Se vuoi vedere dei video di esercizi svolti al riguardo dello studio di una funzione utilizza gratis il mio canale Youtube
\[y=\frac{2x}{x^{2}+x-1},\, \, y=\frac{x(1-2x)}{1+2x},\, \, y=\frac{1}{1+2x},\, \, y\frac{4x^{2}+1}{3x},\, \, y=x+\frac{4}{x^{2}}\]
\[y=\frac{2}{x^{2}},\, \,y=\frac{x^{3}-3x^{2}+4}{x^{2}},\, \, y=\left ( \frac{1}{x}-1 \right )^{2}\]
\[y=\frac{2x^{3}-3x^{2}+1}{2x^{2}},\, \, y=-1+\frac{1}{x}\]
\[y=x^{2}(3-x),\, \, y=xe^{-x},\, \, y=\frac{x^{3}}{2x^{2}-1},…\]
\[y=tan\, x-2sen\, x\, \, in \left [ -\frac{\pi }{2},\frac{3\pi }{2} \right ],\, y=sen\, 2x-tan\, x\, \, \, in\, [0,\pi ],\, \, y=\frac{1+senx}{senx}\, \, in\, \left [ 0,2\pi \right ]\]
\[y=\frac{1}{senx\, cosx}\, \, in\, \left [ 0,2\pi \right ],\, \, y=x\sqrt{1-x^{2}}\]
\[y=\frac{x^{2}}{2}+ln\left | x+1 \right |\]
\[y=sen^{3}x+cos^{3}x\: \: \: in\, \, \, \left [ 0,2\pi \right ]\]
Il grafico di tale funzione inizia nel punto R(0,1) e termina nel punto T(2pi,1) e con l’ausilio della derivata prima y’ = 3senx cosx )( senx – cosx ) si stabilisce che ammette tre minimi relativi e due massimi relativi rispettivamente di ascisse \[x=\frac{\pi }{4},\, \, x=\pi ,\, \, x=\frac{3\pi }{2},\, \, x=\frac{\pi }{2},\, \, x=\frac{5\pi }{4}\] nonchè altri due massimi relativi in x = 0 e x = 2pi (vedi figura 7). Nella figura riportato abbiamo indicato anche i sei punti di flesso calcolabili con la derivata seconda y”=3(senx + cosx)(-1 + 3senxcosx)
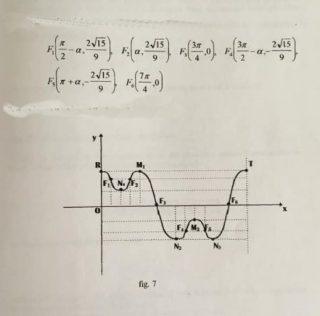
\[y=x^{3}+3x^{2}+3x+1,\, \, \, y=x^{3}-3x^{2}-3x+1\]
\[y=2senx+sen2x\, \, \, in\, \, \left [ 0,2\pi \right ]\]
\[y=sen2x\cdot cosx\, \, \, in\, \, \left [ 0,2\pi \right ]\]
\[y=3cos2x-4 cosx\, \, \, in\, \, \left [ 0,2\pi \right ]\]
\[y=\frac{x^{2}+1}{x^{2}-1},\, \, \, \, y=\frac{1+x^{3}}{x^{2}}\]
\[y=x+sen2x\, \, \, \, in\left [ -2\pi ,2\pi \right ]\]
\[y=\frac{2x-1}{x^{3}}\]
\[y=\frac{1+x^{2}}{1-x^{2}}\]
\[y=x^{2}+\frac{1}{x^{2}}\]
\[y=\frac{6x^{2}+2x+3}{2\left ( 2x^{2}+1 \right )}\]
\[y=x^{2}+\frac{16}{x^{2}}\]
\[y=sen\left ( x+\frac{\pi }{3} \right )+cos\left ( x-\frac{\pi }{6} \right )\]
\[y=e^{2sen\left ( x+\frac{\pi }{3} \right )}\]
\[y=\sqrt{\frac{2-x}{x}}\]
\[y=\frac{1+x^{2}}{x^{2}}\]
\[y=\frac{x}{\sqrt{x-1}}\]
\[y=\left ( 2x^{3}-4x \right )e^{-x^{2}}\]
\[y=\left ( x^{2}-1 \right )e^{-x^{2}}\]
\[y=\left\{\begin{matrix} -3x^{2} +4x&\, se\, \, x\leq 1 \\ \frac{1}{x^{2}} &\, se\, \, x>1 \end{matrix}\right.\]
\[y=\pm 2x\sqrt{1-x^{2}}\]
\[y=\sqrt{\frac{2}{3}\left ( x^{2}-x+1 \right )}\]
\[y=senx+\frac{1}{4senx}\]
\[y=\frac{x^{2}}{4-x^{3}}\]