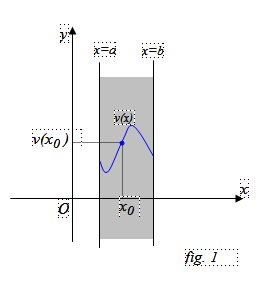
Sia w = f(x , y) una funzione numerica definita nella striscia ( fig. 1) di
, continua in T e lipschitziana* rispetto ad y.
Allora per ogni appartenente ad T esiste una ed una sola soluzione v(x) definita e continua in [a,b] del problema di Cauchy:
Dimostrazione
Cominciamo ad osservare che una funzione v(x) definita e continua in [a,b] è una soluzione del problema di Causchy, (1), se e solo se è del tipo:
—-
*) Lipschitziana:
Dimostrazione