Risoluzione
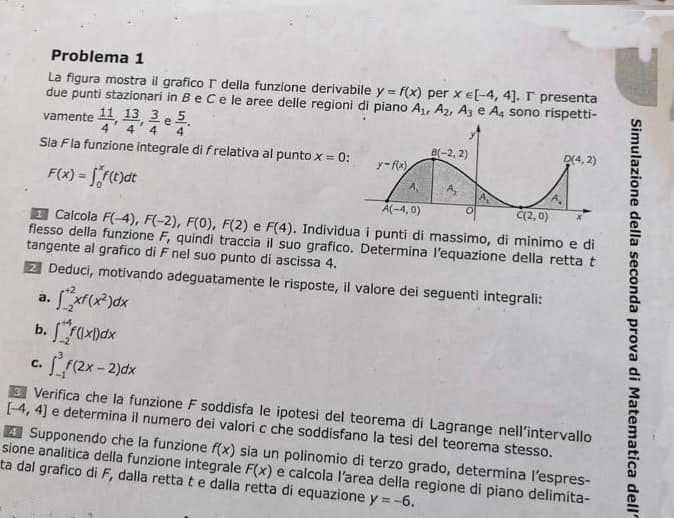
1) Per calcolare F(-4) utilizziamo $ F(x)=\int_{0}^{x}f(t)dt=-\int_{-x}^{0}f(t)dt$, con x >0:
\[F(-4)=-\int_{-4}^{0}f(t)dt=-\left ( A_{1}+A_{2} \right )=-\left ( \frac{11}{4}+\frac{13}{4} \right )=-6\]
analogamente per F(-2):
\[ F(-2)=-\int_{-2}^{0}f(t)dt=-A_{2} =-\frac{13}{4}\]
Calcoliamo F(0), F(2) e F(4)
\[ F(0)=\int_{0}^{0}f(t)dt=0\]
\[ F(2)=\int_{0}^{2}f(t)dt=A_{3} =\frac{3}{4}\]
\[F(4)=\int_{0}^{4}f(t)dt=\left ( A_{3}+A_{4} \right )=\left ( \frac{3}{4}+\frac{5}{4} \right )=2\]
Rappresentando i quattro punti trovati nel piano cartesiano con $-4\leq x\leq 4$ e tenendo conto che F’ = f, e F”=f’ si può accennare il grafico della funzione F(x), con due flessi in x = -2, x = 2 e un massimo in x = 4 con F(4) =2 e un minimo in x = -4 con F(-4) = -6.
La retta tangente t nel punto d’ascissa x = 4 si può calcolare con la formula:
\[ y-y_{0}=m(x-x_{0}), \, \, con\, m = F'(x_{0})\]
e si ha
\[y-2=m(x-4), \, \, con\, m = F'(4)=f(4)=2\]
e quindi la retta tangente t è
\[ y-2=2(x-4)\to y=2x-6\]
2) Il primo integrale vale zero, basta applicare il metodo di sostituzione o far comparire la derivata di $x^{2}$ sotto il simbolo di integrale, il che si ottiene moltiplicando e dividendo per 2:
\[ \int_{-2}^{2}xf(x^{2})dx=\frac{1}{2}\int_{-2}^{2}2xf(x^{2})dx=\left [ \frac{1}{2}\frac{f\left ( x^{2} \right )^{2}}{2} \right ]_{-2}^{2}=\frac{1}{4}\left ( f(4)^{2}-f(4)^{2} \right )=0\]
Il secondo integrale, tenendo presente la definizione di valore assoluto si deve decomporre nella somma di due integrali:
\[\int_{-2}^{4}f(\left|x \right|)dx=\int_{-2}^{0}f\left ( -x \right )dx+\int_{0}^{4}f\left ( x \right )dx=…\]
il secondo integrale vale la somma di $A_{3}+A_{4}=2$, il primo invece si deve trasformare facendo comparire la derivata di -x moltiplicando e dividendo per -1, ottenendo così proprio il valore rappresentato dall’area $A_{2}=13/4$. Pertanto il secondo integrale vale 13/4 +2 = 21/4.
Il terzo integrale si può calcolare per sostituzione ponendo 2x – 2 = t da cui dx = dt/2 e si ha:
\[ \int_{-1}^{3}f(2x-2)dx=\int_{-4}^{4}f\left ( t \right )\frac{dt}{2}=\frac{1}{2}\int_{-4}^{4}f\left ( t \right )dt=4\]
tenendo conto che la somma di tutte le aree al di sotto della curva f(x) è 8.
3) Le ipotesi del teorema di Lagrange sono verificate, essendo la f continua, e quindi deve aversi:
\[ \frac{F(4)-F(-4)}{4-(-4)}=F'(x)\rightarrow \frac{F(4)-F(-4)}{4-(-4)}=f(x)\to \frac{2+6}{8}=f(x)\to f(x)=1\]
e risolvendo graficamente l’equazione f(x) = 1 si vede che vi sono tre punti c che soddisfano nell’intervallo aperto ]-4, 4[ al teorema di Lagrange.
4) Se f(x) è un polinomio di terzo grado allora è del tipo
1) $f(x)=ax^{3}+bx^{2}+cx+d$
e dunque bisogna determinare le costanti reali a, b, c, d. Dalle condizioni assegnate, vedi grafico, bisogna dedurre 4 equazioni indipendenti da mettere a sistema, si possono dedurre osservando che la curva ammette un massimo in B (-2,2) e un minimo in C(2,0) ed inoltre passa anche per i punti (-4,0) e (4,2). Sviluppando tali condizioni si ottengono più equazioni ma ne dobbiamo prendere 4 indipendenti, siano quelle che si deducono da:
f(-4) = 0, f(2) = 0, f'(-2) = 0, f'(2) = 0
la prima è relativa al passaggio della curva f(x) per il punto (-4,0), la seconda è relativa al passaggio della curva per il punto C, la terza è relativa al fatto che in B vi è un massimo relativo e la quarta è relativa al fatto che in C vi è un minimo. Pertanto dalla (1) per f(-4) = 0 si ha l’equazione:
\[ 0=-64a+16b-4c+d\]
per f(2) = 0 sostituendo nella (1) si ha:
\[ 0=8a+4b+2c+d\]
La derivata della (1) è $f'(x)=3ax^{2}+2bx+c$ e dalla condizione f'(-2) = 0 si ottiene:
\[ 0=12a-4b+c\]
e dalla condizione f'(2) = 0 si ottiene:
\[ 0=12a+4b+c\]
Queste quattro equazioni però sono dipendenti perché il determinante del sistema è zero quindi bisogna scartarne una e aggiungere una quarta equazione indipendente dalle altre 3. Scartiamo la quarta equazione e ricerchiamo una quarta condizione sfruttando il fatto che la curva passa per il punto (4,2)
\[ 2=64a+16b+4c+d \]
e mettendo a sistema le prime tre equazioni con questa ultima, e risolto il sistema di 4 equazioni in 4 incognite, si ricavano i valori di a, b, c, d:
\[ a=\frac{1}{16},b=0,c=-\frac{3}{4},d=1\]
Pertanto la funzione f(x) ha espressione
\[ f(x)=\frac{1}{16}x^{3}-\frac{3}{4}x+1\]
e quindi l’espressione analitica della funzione integrale è
\[ F(x)=\int_{0}^{x}\left ( \frac{1}{16}t^{3}-\frac{3}{4}t+1 \right )dt =\frac{1}{64}x^{4}-\frac{3}{8}x^{2}+x\]
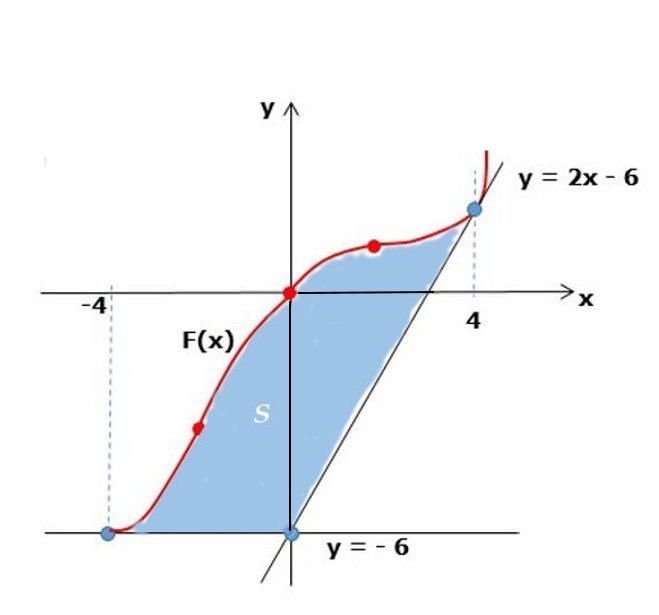
L’area S richiesta (Fig. 1), ovvero la regione finita di piano compresa tra la curva $F(x)=\frac{1}{64}x^{4}-\frac{3}{8}x^{2}+x$, la retta tangente t di equazione y = 2x – 6 e la retta y = – 6 si può calcolare con la formula:
\[S=\int_{-4}^{4}\left ( \frac{1}{64}x^{4}-\frac{3}{8}x^{2}+x \right )dx+\int_{4}^{0}(2x-6)dx+\int_{0}^{-4}-6dx\]
e calcolando separatamente i tre integrali si vede che il primo vale -48/5, il secondo 8 e il terzo 24 e quindi l’area S è 112/5.
1.1.- Vedi il seguente video per un altro esercizio
1.2.- Vedi un altro video di esercizio svolto
2.- Provate a risolvere i seguenti quesiti per la Maturità.
Risoluzione (in preparazione)
1.- Riscrivere l’equazione nel secondo modo \[ e^{2x}=-x^{3}+3\] e intersecare i due grafici delle funzioni:
\[ y=e^{2x},\: \: y=-x^{3}+3\]
ottenendo come unica soluzione dell’equazione il punto $0<x_{o}<\sqrt[3]{3}$.
3.1.- Vedi un altro quesito della Maturità Scientifica… Clicca qui
4.- Problemi con parametri. Esercizi pe la Maturità

Risolviamo il secondo esercizio con 4 parametri.
Data la funzione
\[y=ax+b+\frac{c}{x}+\frac{d}{x^{2}}\]
scriviamo quattro equazioni nelle incognite a, b, c, d sfruttando i dati del problema e determiniamo tali parametri mettendo poi a sistema le quattro equazioni determinate.
\[ y'(1)=0\to y’=a+0-\frac{c}{x^{2}}-2\frac{d}{x^{3}}\to y'(1)=a-c-2d\to a-c-2d=0\]
\[y”(-2)=0\to y”=2\frac{c}{x^{3}}+6\frac{d}{x^{4}}\to\, \, -\frac{c}{4}+3\frac{d}{8}=0\to 2c-3d=0\]
Altre due equazioni si deducono dal fatto che l’asintoto obliquo è $2y+x+4=0\to y=-\frac{x}{2}-2$
Problema assegnato alla Maturità 2022
La funzione assegnata è \[ f(x)=\frac{a+b\cdot lnx}{x}\]