A) Area del rettangoloide o trapezoide.
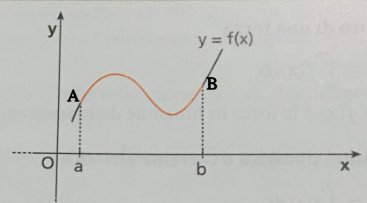
Sia y = f(x) una funzione definita, continua e non negativa nell’intervallo chiuso [a,b] di R.
L’area S del rettangoloide ABCD ( fig. 1) delimitata dalla curva y = f(x), dall’asse x e dalle rette x = a ed x = b è:
\[1)\, \, \, \, \,\, \, \, S=\int_{a}^{b}f(x)dx\]
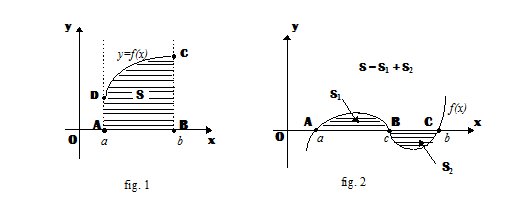
Nel caso la curva d’equazione y = f(x) sia situata nell’intervallo chiuso [a,b] sia al di sopra che al di sotto dell’asse x (fig. 2) si ha:
\[2)\, \, \, \, \,\, \, \, S=S_{1}+S_{2}=\int_{a}^{c}f(x)dx+\int_{c}^{b}-f(x)dx=\int_{a}^{c}f(x)dx-\int_{c}^{b}f(x)dx=\]
B) Area di una regione di piano compresa tra due o più curve. Siano y = f(x) e y = h(x) due funzione definite, continue e non negative nell’intervallo chiuso [a,b] e tali che \[f(x)\geq h(x),\, \, \, \, \, \forall x\in \left [ a,b \right ]\]
L’area S della regione finita di piano delimitata dalle due curve e dalle rette x = a ed x = b è:
\[3)\, \, \, \, \, \, \, \, \, \, \int_{a}^{b}\left ( f(x)-h(x) \right )dx\]
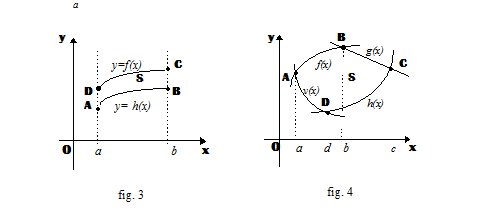
Nel caso particolare rappresentato in figura 4 l’area dellla figura convessa ABCD determinata dalle funzioni y = f(x), y = g(x), y= h(x), y= v(x) definite e continue rispettivamente negli intervalli [a,b] [b,c] [c,d] [d,a] si può calcolare l’area S mediante la formula:
\[4)\: \: \: \: \: S=\int_{a}^{b}f(x)dx+\int_{b}^{c}g(x)dx+\int_{c}^{d}h(x)dx+\int_{d}^{a}v(x)dx\]
C1 ) Volume di un solido di rotazione intorno all’asse x.
Sia y = f(x) una funzione definita e continua in [a,b] e tale che \[f(x)\geq 0\: \: \: \: \forall x\in \left [ a,b \right ]\]
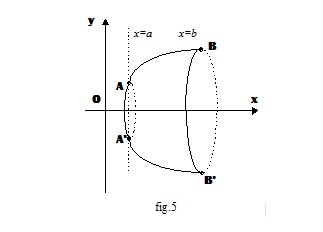
Il volume V del solido (fig. 5) ottenuto facendo ruotare di 360° il trapezoide definito dalla curva y = f(x) intorno all’asse x, e delimitato dai piani ortogonali all’asse x passanti per i punti A(a,0) e B(b,0) è dato dalla formula:
\[5)\: \: \: \: \: V=\pi \int_{a}^{b}\left [ f(x) \right ]^{2}dx\]
C2) Volume di un solido di rotazione intorno all’asse y.
Il volume V del solido (fig. ) ottenuto facendo ruotare di 360° il trapezoide definito dalla curva x = f(y) (positiva o nulla) intorno all’asse y, e delimitato dalle rette y = a e y = b è dato dalla formula:
\[6)\: \: \: \: \: V=\pi \int_{a}^{b}\left [ f(y) \right ]^{2}dy\]
C3) Volume di un solido di rotazione intorno all’asse y.
Il volume V del solido (fig. ) ottenuto facendo ruotare di 360° il trapezoide definito dalla curva y = f(x) (positiva o nulla) intorno all’asse y, e delimitato dalle rette x = a e x = b, con a e b concordi, è dato dalla formula:
\[7)\: \: \: \: \: V=2\pi \int_{a}^{b}\left [ xf(x) \right ]dx\]
C4) Volume di un solido di rotazione con il metodo delle sezioni.
Il volume V del solido (fig. ) ottenuto facendo ruotare di 360° una sezione del solido S(x), funzione,che esprime l’area della generica sezione del solido al variare di x, perpendicolare all’asse x, è dato dalla formula:
\[8)\: \: \: \: \: V= \int_{a}^{b} S(x) dx\]
D) Lunghezza di un arco di curva. Sia y = f(x) una funzione definita e derivabile in [a,b] e tale che \[f(x)\geq 0\: \: \: \: \forall x\in \left [ a,b \right ]\]. La lunghezza L di un arco di curva di estremi A (a, 0) e B (b,0) si può calcolare con la formula:
\[L_{AB}=\int_{a}^{b}\sqrt{1+f'(x)^{2}}dx\]
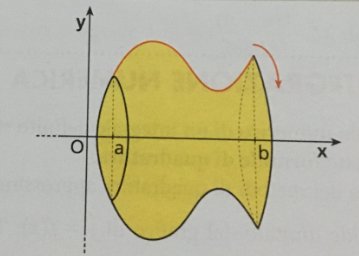
E) Area di una superficie di rotazione.- Sia y = f(x) una funzione definita e continua in [a,b] e tale che \[f(x)\geq 0\: \: \: \: \forall x\in \left [ a,b \right ]\]. L’area A della superficie di un solido di rotazione ottenuta facendo ruotare di 360 gradi la curva y =f(x) intorno all’asse x si può calcolare con la formula:
\[A=2\pi \int_{a}^{b}f(x)\sqrt{1+f'(x)^{2}}dx\]
Esempio 1.1.- Area di una regione finita di piano.- Determinare l’area della parte di piano compresa tra la curva di equazione $\displaystyle y=x^{3}$, l’asse x e la retta x = 2.
Risoluzione
Come primo passo bisogna costruire la figura (fig. 6), disegnando in un piano Oxy la curva d’equazione y = x^3 , l’asse x e la retta x = 2.
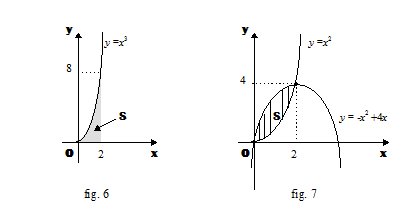
Quindi si individuano la regione finita di piano richiesta, gli estremi d’integrazione x = 0 e x = 2, e si calcola l’area: \[S=\int_{0}^{2}x^{3}dx=\left [ \frac{x^{4}}{4} \right ]_{0}^{2}=\frac{2^{4}}{4}-\frac{0^{4}}{4}=\frac{16}{4}=4\]
Esempio 1.2.- Determinare l’area della parte di piano delimitata dalle curve di equazioni \[y=x^{2},\, \, \, \, y=-x^{2}+4x\]
Risoluzione
Costruita la figura (fig. 7) si vede che l’area S è data da: \[S=\int_{0}^{2}(-x^{2}+4x)dx-\int_{0}^{2}x^{2}dx=\frac{8}{3}\]
Esempio 1.3.1.- Determinare l’area della parte di piano delimitata dalla curva $y=-x^{2}+5x-4$ e dalla tangente alla curva nel suo punto di ascissa x = 2.
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube.
Esempio 1.3.2.- Un altro esercizio svolto? Vedi questo mio video
Esempio 1.4.- Determinare l’area della parte di piano compresa tra le curve di equazione $y=4x,\, \, y=-\frac{1}{4}x^{2}+2x,\, \, y = – 2x+12$
Risoluzione
L’area S della figura convessa OAV (fig. 8) si può calcolare nel seguente modo:
\[S=\int_{0}^{2}4xdx-\int_{2}^{4}(-2x+12)dx+\int_{4}^{0}\left ( -\frac{1}{4}x^{2}+2x \right )dx=\frac{124}{3}\]
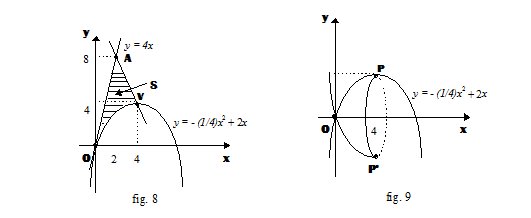
Esempio 1.5.- Determinare l’area della parte di piano compresa tra le curve di equazioni $\displaystyle y=x^{2},\, \, y=-2x+8,\, \, \, y=\frac{1}{2}x^{2}+8$ nell’intervallo [- 4, 2]. Calcolre inoltre l’area della regione finita di piano situata nel primo quadrante e compresa tra la parabola non passante per l’origine la retta y = -2x + 8, la retta x = 2.
Risoluzione
Disegnate le tre curve nello stesso piano cartesiano (vedi figura) si calcola l’area richiesta:
\[A_{tot}=A_{2}+A_{3}=\frac{92}{3}\]
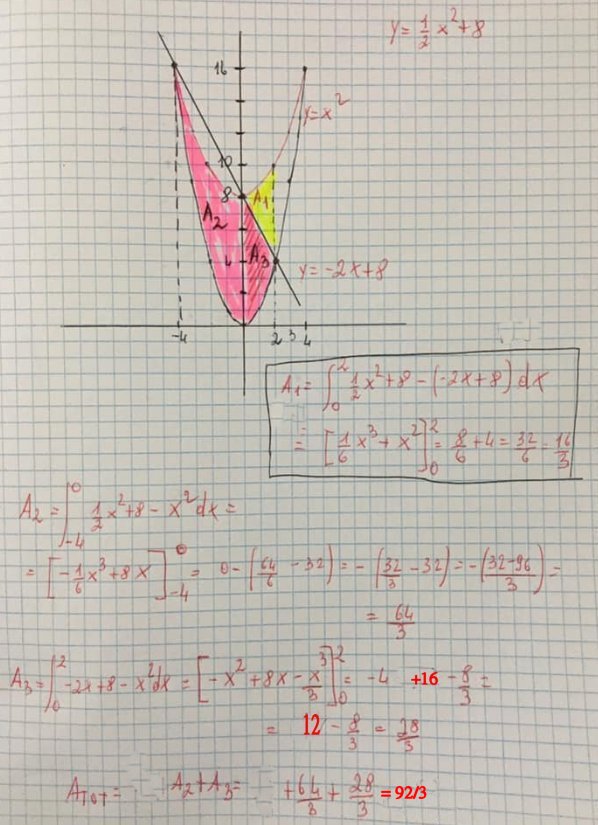
Per rispondere alla seconda domanda bisogna calcolare l’area $\displaystyle A_{1}$ , in giallo.
Esempio 1.6.- Determinare l’area della parte di piano compresa tra le curve di equazioni $\displaystyle y=x^{2},\, \, y=-2x+8,\, \, \, y=\frac{1}{2}x^{2}+8$ e situata nel primo quadrante del piano cartesiano.
Non sai calcolarla? Allora vedi il mio video su Youtube
Esempio 2.1.- Lunghezza di un arco di cruva.- Determinare la lunghezza del contorno del triangolo mistilineo VPT determinato dalle curve $\displaystyle y=x^{2},\, \, y=-2x+8,\, \, \, y=\frac{1}{2}x^{2}+8$ e situato nel primo quadrante.
Non sai calcolarla? Allora vedi il mio video su Youtube
Esempio 3.1.- Volume di un solido di rotazione e area della superficie di rotazione.- Determinare il volume V del solido ottenuto facendo ruotare di 360° l’arco OP della parabola d’equazione $\displaystyle y=-\frac{1}{4}x^{2}+2x$, ove P è il vertice della parabola, intorno all’asse x.
Risoluzione
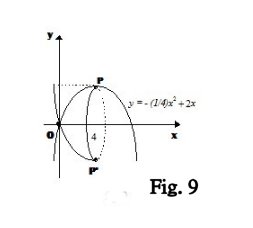
Il volume V del solido (fig. 9) OPP’ è dato da: \[V=\pi \int_{0}^{4}\left ( -\frac{1}{4}x^{2}+2x \right )dx=32\pi\]
Esempio 3.2.- Determinare il volume V del solido ottenuto facendo ruotare di 360° la retta d’equazione y = 2x + 1 intorno all’asse x. Detterminare inoltre l’area della superficie di rotazione.
Esempio 3.3.- Determinare il volume V del solido ottenuto facendo ruotare di 360° la parte di piano compresa tra la retta e la parabola rispettivamente di equazioni $\displaystyle y=-2x+8,\, \, \, y=\frac{1}{2}x^{2}+8$, indicate nell’Esempio 1.5.
Esempio 4.1.- Volumi di solidi che ruotano intorno all’asse y. Determinare il volume V del solido ottenuto facendo ruotare di 360 intorno all’asse y la curva d’equazione $\displaystyle x=\sqrt{y}$ e delimitato alle rette y = 1, y = 3.
Esempio 4.2.- Determinare il volume V del solido ottenuto facendo ruotare di 360 intorno all’asse y la curva d’equazione $\displaystyle y=x-\frac{x^{2}}{3}$ e dall’asse x.
Esempio 4.3.- Determinare il volume V del solido ottenuto facendo ruotare di 360 intorno all’asse y il trapezoide delimitato dalla curva d’equazione $x=9-y^{2}$ dall’asse y e dalla retta y =3x/5-1 e situato al di sopra dell’asse x.
Risoluzione
Il volume si può calcolare come quello di un tronco di cono sommato a quello del solido ottenuto facendo ruotare l’arco di parabola intorno all’asse y tra y = 2 e y = 3.
Risultato (4492/135)$\pi$
Esempio 4.4.- Data la parabola $\displaystyle y=-x^{2}+4x$ definita nell’intervallo [0, 4] e sia S la la regione di piano che la parabola delimita nell’intervallo dato con l’asse x. Calcolare il volume del solido che ha come base S(x) e le cui sezioni con piani perpendicolari all’asse x sono quadrate.
Esempio 5.- Esercizi di vario tipo.- Si può chiedere prima di tutto di studiare una funzione e rappresentarla nel piano e poi calcolare un’area finita di piano o un volume. E’ il caso di questo video, inserito nel mio canale Youtube.
