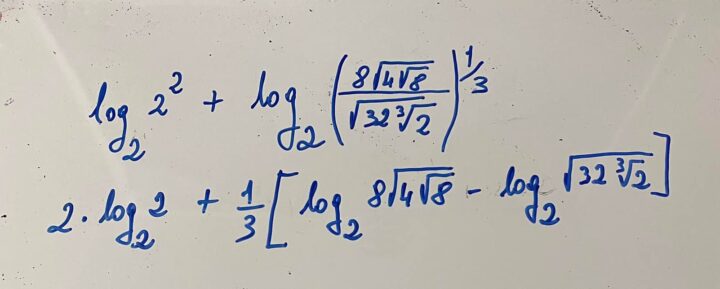Dato un numero reale positivo a e diverso da 1 e un numero reale positivo b, si dice logaritmo in base a di b il numero reale x tale che:
\[a^{x}=b\]
con \[a\in R^{+}-\left \{ 1 \right \},b\in R^{+}\]
Quindi per definizione risulta:
\[a^{x}=b\Leftrightarrow x=log_{a}b\]
Se non hai capito vedi il mio video nel mio canale Youtube
Se a = e (numero irrazionale di Nepero e = 2,71…) il logaritmo si dice naturale o neperiano, mentre se a = 10 il logaritmo si dice decimale.
Il logaritmo neperiano di b si indica con ln b (o con log b, poco usato), mentre il logaritmo decimale si indica con log b (o con Log b, poco usato).
Teoremi
Teorema del prodotto
\[log_{a}\left ( xy \right )=log_{a}\, x+log_{a}\, y\]
Teorema del rapporto
\[log_{a}\left ( \frac{x}{y} \right )=log_{a}\, x-log_{a}\, y\]
Teorema della potenza
\[log_{a}\left ( x^{p} \right )=p\cdot log_{a}\left ( x \right )\]
\[log_{a}\left ( \sqrt[n]{x}\, \right )=\frac{1}{n}\cdot log_{a}\left ( x \right )\]
Formula di cambiamento di base: da base a alla base c:
\[log_{a}\left ( b \right )=\frac{log_{c}\left ( b \right )}{log_{c}\left ( a \right )}\]
Proprietà elementari
\[log_{a}\left ( a \right )=1,log_{a}\left ( 1 \right )=0,log_{a}\left ( \frac{1}{a} \right )=-1,log_{\frac{1}{a}}\left ( a \right )=-1\]
Identità
\[log_{a}\left (a^{p} \right )=p,\, \, \, \forall p\in R\]
\[a^{log_{a}\left ( p \right )}=p,\, \, \forall p>0\]
Esempio 1.1.- Calcolare i seguenti logaritmi
\[log_{2}\, 8,\, \, log_{3}\, \frac{1}{3},\, \, log_{6}\, \frac{1}{36},\, \, log_{4}\, 2,log_{4}32,log_{3}\frac{1}{27},log_{16}\frac{1}{4},log_{5}\, \sqrt[3]{5},\]
Risoluzione
Si ha:
\[log_{2}\, 8=log_{2}\, 2^{3}=3\]
\[log_{3}\, \frac{1}{3}=log_{3}\, 3^{-1}=-1\]
\[log_{6}\, \frac{1}{36}=log_{6}\, 6^{-2}=-2\]
Utilizziamo la definizione di logaritmo:
\[log_{4}\,2=x\rightarrow 4^{x}=2\rightarrow 2^{2x}=2\rightarrow 2x=1\rightarrow x=1/2\]
…
Esempio 1.2.- Calcolare i seguenti logaritmi utilizzando il teoremi sui logaritmi \[log_{2}\, \, 4\cdot \sqrt[3]{\frac{8\sqrt{4\sqrt{8}}}{\sqrt{32\sqrt[3]{2}}}}\]
\[ln\, \, e^{2}\cdot \sqrt[5]{\frac{e\sqrt{6\sqrt{e^{3}}}}{\sqrt{4\sqrt[3]{e}}}}\]
Calcolo del primo logaritmo
Applicando il teorema del prodotto possiamo riscrivere il primo logaritmo nel seguente modo:
\[log_{2}\, \, 4+log_{2} \sqrt[3]{\frac{8\sqrt{4\sqrt{8}}}{\sqrt{32\sqrt[3]{2}}}}\]
da cui, applicando prima il teorema della potenza e poi quello de rapporto, si ha
e applicando il teorema del prodotto si ottiene:
\[2(1)+\frac{1}{3}\left [ log_{2}8+log_{2}\sqrt{4\sqrt{8}}-log_{2}\sqrt{32\sqrt[3]{2}} \right ]\]
ossia:
\[2+ \frac{1}{3}\left [ log_{2}8+log_{2}\left ( 4\sqrt{8} \right )^{\frac{1}{2}}-log_{2}\left ( 32\sqrt[3]{2} \right )^{\frac{1}{2}} \right ]\]
e per il teorema della potenza:
\[ 2+\frac{1}{3}\left [ log_{2}2^{3}+\frac{1}{2}log_{2}\left ( 4\sqrt{8} \right )-\frac{1}{2}log_{2}\left ( 32\sqrt[3]{2} \right ) \right ]\]
\[ 2+\frac{1}{3}\left [3 log_{2}2+\frac{1}{2}log_{2}\left ( 4\sqrt{8} \right )-\frac{1}{2}log_{2}\left ( 32\sqrt[3]{2} \right ) \right ]\]
ossia:
\[ 2+\frac{1}{3}\left [ 3+\frac{1}{2}log_{2}\left ( 4\sqrt{8} \right )-\frac{1}{2}log_{2}\left ( 32\sqrt[3]{2} \right ) \right ]\]
continua…
Esempio 1.3.- Scrivere i seguenti logaritmi nella nuova base c indicata a fianco:
\[log_{2}\, 24,\, \, c=6\]
\[log_{32}\, 12,\, \, c=8\]
\[log_{\frac{1}{2}}\, \frac{4}{5},\, \, c=2\]
Risoluzione
\[log_{2}\, 24=\frac{log_{6}\, 24}{log_{6}\, 2}=…\]
Esempio 1.4.- Scrivere i seguenti logaritmi nella nuova base c ( 10 o e) e calcolarli con l’uso della calcolatrice scientifica con cinque cifre decimali:
\[log_{3}\,7,\, log_{13}\,\, 35,\, \, log_{32}\, 8\]
Risoluzione
Trasformiamo a base dieci e si ha:
\[log_{3}\, 7=\frac{log_{}\, 7}{log_{}\, 3}=\frac{0,84509}{0,47712}=1,77123\]
Trasformiamo a base naturale (e), si ha:
\[log_{13}\, 35=\frac{ln\, 35}{ln\, 13}=\frac{3,55534}{2,56494}=1,38612\]