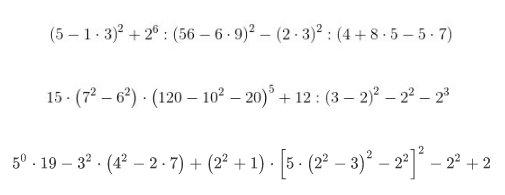
Esempio 1.1.- Espressioni con numeri naturali (N). Calcolare il valore delle seguenti espressioni:
![]()
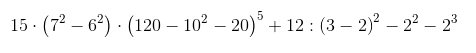
\[5^{0}\cdot 19-3^{2}\cdot \left ( 4^{2} -2\cdot 7\right )+\left ( 2^{2}+1\right )\cdot \left [ 5\cdot \left ( 2^{2}-3 \right )^{2}-2^{2} \right ]^{2}-2^{2}+2\]
![]()
\[2^{123}\cdot 2^{300}:2^{323}+100^{34}\cdot 100^{120}:100^{152}\]
Osservazione 1.- Per raggruppare un insieme di operazioni si usano le parentesi tonde, quadre o graffe:
( , [ , { aperte; ), ] , } chiuse.
Nei calcoli di espressioni numeriche o algebriche si eseguono sempre per prima le operazioni in parentesi tonde, poi quelle nelle parentesi quadre ed infine quelle nelle parentesi graffe.
Inoltre, in un’espressione in cui non figurano parentesi si eseguono le operazioni nell’ordine indicato, ovvero prima l’operazione che si incontra per prima, se sono dello stesso grado*, mentre se non sono dello stesso grado si segue il seguente ordine:
- potenze ed estrazioni di radice;
- moltiplicazioni e divisioni;
- addizioni e sottrazioni.
*) Sono, ad esempio, dello stesso grado la moltiplicazione e la divisione, mentre sono di grado diverso la potenza e la moltiplicazione oppure la divisione e la sottrazione.
Esempio 2.1.- Operazioni con numeri interi (Z). Calcolare il valore delle seguenti operazionii:
Vedi il mio video su Youtube
Esempio 2.1.- Potenze con numeri interi (Z). Calcolare il valore delle seguenti potenze:\[\left ( -2 \right )^{3},\, \, \left ( -3 \right )^{4},\, \, \left ( +2 \right )^{5},\, \, \left ( +3 \right )^{2},\, \left ( -5 \right )^{0}\]
\[-2\cdot \left ( -2 \right )^{3}\cdot \left ( -2 \right )^{4}-\left ( 2 \right )^{3}\cdot 2^{4}\]
\[\left \{ \left [ \left ( -2\cdot \left ( -10 \right )^{15}\cdot \left ( -10 \right )^{44}-\left ( 10 \right )^{35}\cdot 10^{24} \right )^{2}+2 \right ] +2-10^{49}\right \}^{2\cdot \left ( -2+3 \right )^{2}}\]
Esempio 2.3.- Espressioni con numeri interi (Z). Calcolare il valore delle seguenti espressioni:
\[+1+\left ( +5-6+12\cdot 3 \right )-3\left ( 2-4+5 \right )-2^{3}\cdot 4\]
\[-2\cdot \left \{ -11\cdot 3^{2}-2\cdot \left ( 6-12 \right )^{2} -3\cdot \left [ -2\left ( 2-4+5 \right )-3^{2}\cdot 3^{3}:3^{4} \right ]\right \}-2:3^{2}\cdot 3\]
Esempio 3.1.- Espressioni con numeri razionali (Q). Calcolare il valore delle seguenti espressioni:
\[-2-3-\left [ \left ( -\frac{1}{6}+\frac{1}{4} \right )-\frac{2}{3} \right ]-\left \{ -\frac{5}{2}-\left [ -2+\frac{1}{2}+\left ( \frac{5}{3}-1 \right ) \right ] \right \}:2-3\cdot \frac{2}{5}\]
\[\left ( -1+\frac{1}{2} \right )^{2}-\left \{ \left [ \left ( -1-\frac{1}{4} \right )^{3}:\left ( \frac{3}{4}-2 \right )^{2}+\left ( -\frac{7}{6} \right )^{3}\cdot \left ( \frac{11}{4}-1 \right )^{3} \right ]^{2}:\left [ \left ( -2 \right )^{-1} \right ]^{2}+\frac{3}{4} \right \}:\left ( \frac{8}{7} \right )^{-2}+\frac{1}{3}\]
Esempio 3.2.- Calcolare il valore delle seguenti espressioni:
\[\left [ \left ( -\frac{3}{4} \right )^{-2} \right ]^{-2}\cdot \left ( \frac{4}{3} \right )^{-3}:\left ( -\frac{3}{4} \right )^{5}+\left [ \left ( -\frac{3}{4} \right )^{5} :\left ( \frac{4}{3} \right )^{-2}\right ]\cdot \left ( \frac{3}{4} \right )^{-3}\]
\[\left ( 4+\frac{1}{2} \right )^{-2}:\left ( 1-\frac{1}{9} \right )^{2}+\left ( -2 \right )^{-3}-\left [ \left ( -\frac{2}{3} \right )^{-4} :\left ( \frac{9}{4} \right )^{-2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{2^{-3}}{5}\right ]-\left ( -\frac{2}{5} \right )^{-2}\cdot 5^{-1}\]
Risoluzione
Calcoliamo il valore della seconda espressione. Si ha:
\[\left ( \frac{9}{2} \right )^{-2}:\left ( \frac{8}{9} \right )^{2}+\left ( -\frac{1}{2} \right )^{3}-\left [ \left ( -\frac{3}{2} \right )^{4} :\left ( \frac{4}{9} \right )^{2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{2^{-3}}{5}\right ]-\left ( -\frac{5}{2} \right )^{2}\cdot 5^{-1};\]
\[\left ( \frac{2}{9} \right )^{2}:\left ( \frac{8}{9} \right )^{2}+\left ( -\frac{1}{8} \right )-\left [ \left ( +\frac{3}{2} \right )^{4} :\left ( \frac{4}{9} \right )^{2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{2^{-3}}{5}\right ]-\left ( +\frac{5}{2} \right )^{2}\cdot\frac{1}{5};\]
\[\left ( \frac{2}{9}:\frac{8}{9} \right )^{2}-\left ( \frac{1}{8} \right )-\left [ \left ( \frac{9}{4} \right )^{2} :\left ( \frac{4}{9} \right )^{2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{1}{8}\cdot \frac{1}{5}\right ]-\left ( \frac{25}{4} \right )\cdot\frac{1}{5};\]
\[\left ( \frac{2}{9}\cdot \frac{9}{8} \right )^{2}-\frac{1}{8}-\left [ \left ( \frac{9}{4}:\frac{4}{9} \right )^{2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{1}{40}\right ]- \frac{25}{4}\cdot\frac{1}{5};\]
\[\left ( \frac{1}{4}\right )^{2}-\frac{1}{8}-\left [ \left ( \frac{9}{4}\cdot \frac{9}{4} \right )^{2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{1}{40}\right ]- \frac{5}{4};\]
\[\frac{1}{16}-\frac{1}{8}-\left [ \left ( \frac{81}{16} \right )^{2}\cdot \left ( -\frac{2}{3} \right )^{7}-\frac{1}{40}\right ]- \frac{5}{4};\]
\[\frac{1}{16}-\frac{1}{8}-\left [ \left ( \frac{3^{4}}{2^{4}} \right )^{2}\cdot \left ( -\frac{2^{7}}{3^{7}} \right )-\frac{1}{40}\right ]- \frac{5}{4};\]
\[\frac{1}{16}-\frac{1}{8}-\left [ \left ( \frac{3^{8}}{2^{8}} \right )\cdot \left ( -\frac{2^{7}}{3^{7}} \right )-\frac{1}{40}\right ]- \frac{5}{4};\]
\[\frac{1}{16}-\frac{1}{8}-\left [ -\frac{3}{2} -\frac{1}{40}\right ]-\frac{5}{4};\]
continua da solo…. (che scherzo che ti faccio!)
Esempio 4.1.- Trasformazione in frazione di un numero decimale limitato, periodico semplice e periodico misto. Trasformare i seguenti numeri decimali in frazioni:
\[32,586;\, \, \, 0,76;\, \, 2,\overline{3};\, \, 0,\overline{51};\, 714,3\overline{6};\, \, 0,16\overline{54}\]
\[5,\overline{9};\, \, 0,\overline{9};\, \, \, 310400,\overline{9}\]
Non sai trasformare i numeri decimali in frazioni? Allora vedi il mio video sul mio canale Youtube
Risoluzione
Si tratta di numeri decimali limitati:
\[32,586=\frac{32586}{1000}=\frac{16293}{500};\, \, 0,76=\frac{76}{100}=\frac{19}{25}\]
Si tratta di numeri decimali periodici semplici:
\[2,\overline{3}=\frac{23-1}{9}=\frac{22}{9};\, \, 0,\overline{51}=\frac{51-0}{9}=…\]
Si tratta di numeri decimali periodici misti:
\[714,3\overline{6}=\frac{1236-123}{90}=\frac{1113}{90}=\frac{371}{30}\]
…
Si tratta di numeri periodici semplici con periodo nove:
\[5,\overline{9}=\frac{59-5}{9}=\frac{54}{9}=6;\]
…
Esempio 4.2.- Espressioni con numeri decimali, periodici semplici e misti. Calcolare il valore delle seguenti espressioni:
\[1,2+3,\overline{4}+\frac{1}{2}-2,3\overline{5}\cdot \left ( 1-\frac{2}{3}+0,\overline{3}\right )+4,\overline{5}:1,5\overline{3}\]
\[\left \{ 0,5+\left ( -\frac{6}{5} \right )^{-2}:\left [ -\left ( 1,5 \right )^{-3}\cdot \left ( 1+\frac{1}{2} \right )^{2}-3,\overline{3}:\left ( 1+\frac{2}{3} \right ) \right ]^{2} \right \}^{0}:(-1):\left ( -1+2-3 \right )^{2}\cdot \left ( -\frac{19}{6} \right )\cdot \left ( 2-\frac{2}{19} \right )\]
Esempio 5.1.- Espressioni con le radici quadrate. Calcolare il valore delle seguenti espressioni:
\[\frac{\sqrt{2^{123}\cdot 2^{300}:2^{323}\cdot 100^{34}\cdot 100^{120}:100^{152}}}{\sqrt{2^{92}\cdot 2^{32}:2^{28}\cdot 25}}\]
\[\sqrt{\frac{\frac{1}{2}}{\frac{2}{5}}\cdot \frac{3}{5}:\frac{1}{3}}:\frac{\sqrt{1-\frac{9}{25}}}{\frac{1}{2}-1}\cdot \sqrt{2-\frac{2}{9}}\]
Esempio 6.1.- *** Espressioni con le poteze di difficoltà più elevata
\[\left ( 2^{6} -2^{7}+2\right )^{2}-\left [ \left ( 2^{10}-2^{8} \right )\left ( 2^{10}+2^{8} \right )+\left ( -2^{4} \right )^{5} \right ]:2^{7}-2^{8}\cdot \left ( 1+2^{4} \right )\]
\[\left [ \left ( 2^{24}-2^{23} \right )^{-2}-\left ( -2^{15}+2^{14} \right )^{-2} \right ]:\left [ 1+\left ( -2^{6} \right )^{3} \right ]:\frac{2^{-12}}{2^{36}}\]
Risoluzione
Calcolo della prima espressione.- Conviene sviluppare con la regola del quadrato del trinomio
$\displaystyle \left ( A+B+C \right )^{2}=A^{2}+B^{2}+C^{2}+2AB+2AC+2BC$
la prima potenza al quadrato e poi applicare le regole delle potenze. Si ha
\[2^{12}+2^{14}+2^{2}-2\cdot 2^{6}\cdot 2^{7}+2\cdot 2^{6}\cdot 2-2\cdot 2^{7}\cdot 2-\left [ 2^{20}-2^{16} -2^{20}\right ]:2^{7}-2^{8}-2^{12}\]
da cui
\[2^{12}+2^{14}+2^{2}-2^{14}+2^{8}-2^{9}+2^{16}:2^{7}-2^{8}-2^{12}\]
e sommando i termini simili, ovvero le potenze uguali, si vede che il risultato è: 4.
