$$ e^{iπ}+1=0 $$
$$ y=sen^{3}x+cos^{3}x $$
Risolvere senza utilizzare carta e penna i seguenti quesiti. Questo tipo di test permette di allenare il colpo d’occhio matematico, ossia di ripassare le tecniche rapide di risoluzione, basate sulla conoscenza delle definizioni principali e sulle delle proprietà degli oggetti matematici.
Parte I
- Eseguire il seguente calcolo: 2 + 2 × 2 : 2 – 2 × 2 × 2.
- Eseguire il seguente calcolo: 3 × 4 : 4 × 3.
- Eseguire il seguente calcolo: \[3^{2}\cdot 4^{2}:4\cdot 3\cdot 3^{3}\]
- Eseguire il seguente calcolo:\[\left [ \frac{\left ( ab \right )^{2}}{a} \right ]^{4}\cdot \frac{a^{3}}{\left ( ab \right )^{2}}\]
- Eseguire il seguente calcolo: \[\left [ \left ( 1+\frac{1}{3} -\frac{4}{5}\right ) +1-2\right ]^{0}\]
- Eseguire il seguente calcolo:\[\frac{x}{x-1}\cdot \frac{3}{x+1}\cdot \frac{x^{2}-1}{3x}\]
- Eseguire il seguente calcolo: \[\sqrt{\sqrt{\left ( -\frac{1}{4} \right )^{4}}}\]
- Eseguire il seguente calcolo: \[\sqrt[3]{3}\cdot \sqrt{3}\cdot \sqrt{3}\cdot \sqrt[3]{3}\]
- Eseguire il seguente calcolo: \[\left ( \sqrt[3]{3}\cdot \sqrt{3}\right ):\left ( \sqrt{3}\cdot \sqrt[3]{3} \right )\]
- Eseguire il seguente calcolo: \[2^{\frac{1}{3}}\cdot 3^{\frac{1}{3}}:2+3^{\frac{1}{3}}\cdot 2^{\frac{1}{3}}\]
- Confrontare i seguenti numeri: \[4\cdot 10^{33},\, \, 10^{-11},\, \, -10^{65},\, \, 10^{0}\]
- Confrontare i seguenti numeri reali: \[\frac{\sqrt{3}}{2},\, \, \pi ^{-1},\, \, log\, 1,\, e^{2},\, log_{2}\, 3,\, \, log_{2}4\]
- Confrontare i numeri reali: \[\sqrt{3}, \sqrt{2},\pi ^{3},e^{3},\sqrt{\frac{1}{2}},\sqrt{\frac{1}{3}},\pi ^{4},4^{\pi },e^{e}\]
- Confrontare i numeri reali: \[\frac{2+\sqrt{3}}{5},\frac{3}{4},\sqrt[3]{4},\sqrt[5]{7}\]
.
Parte II
- Verificare se: \[(3^{log_{3}2})^{log_{2}2^{3}}=8\]
- Verificare se: \[\left (ln\, e^{4} \right )^{4^{log_{4}2}}=16\]
- Verificare se: \[log\, 4+log\, 2+log\, 1-log\, 11=0\]
- Verificare se: \[log\, 4+log\, 2+log\, 5-log\, 40=0\]
- Verificare se: $\displaystyle \left ( \sqrt{2} \cdot \sqrt[3]{2}\, \cdot\sqrt[4]{2}\cdot \sqrt[5]{2} \right )^{\frac{5}{6}}$ .
- Qual è la soluzione dell’equazione di primo grado nella sola incognita x: $\displaystyle -3x=0?$
- Risolvere la disequazione: $\displaystyle -7x\left ( x^{2}+1 \right )<0$
- Il sistema $\displaystyle \left\{\begin{matrix} x+y &=1 \\ 2x+2y &=2 \end{matrix}\right.$ ammette soluzione?
- Risolvere la disequazione: $\displaystyle \frac{3\left ( x^{2}+4 \right )}{\sqrt{7}}>0$
- Risolvere la disequazione: $\displaystyle \left ( x-1405 \right )^{4}>0$
- Risolvere la disequazione: $\displaystyle \left ( x-5 \right )^{3}>0$
- Risolvere la disequazione: $\displaystyle -3\left ( x+1 \right )^{2}>0$
- Risolvere la disequazione: $\displaystyle \left | x \right |+1>0$
- Stabilisci senza risolvere una soluzione dell’equazione: $\displaystyle 10^{x}=x^{100}$
Parte III
- Risolvere la disequazione: $\displaystyle \left | x \right |>4$
- Risolvere la disequazione: $\displaystyle \left | x \right |<4$
- Risolvere l’equazione: $\displaystyle \left | x \right |=4$
- Risolvere l’equazione: $\displaystyle \left | x-2 \right |=0$
- Risolvere l’equazione: $\displaystyle \left | x^{2}+12 \right |=0$
- risolvere l’equazione: $\displaystyle \left ( x^{2}+1 \right )^{5}+3=0$
- Risolvere l’equazione: $\displaystyle \left ( x^{2}-1 \right )^{5}+1=0$
- Risolvere l’equazione: $\displaystyle \left ( x-1 \right )^{3}=\frac{1}{4}$
- Risolvere la disequazione: $\displaystyle \sqrt{x^{2}+2}>0$
- Risolvere la disequazione: $\displaystyle \sqrt{x^{2}-2}>0$
- Risolvere l’equazione: $\displaystyle \frac{3x\left ( x^{2}+4 \right )\left ( x^{2}+1\ \right )}{\sqrt{5}+4}=0$
- Stabilire le soluzioni del sistema: $\displaystyle \left\{\begin{matrix} 4x+5 &>2x+6 \\ x^{2}+1 &>2x-3 \\ 10 &>2 \end{matrix}\right.$
- Stabilire le soluzioni del sistema: $\displaystyle \left\{\begin{matrix} 4x+5 &>2x+6 \\ x^{3}+1 &>2x-3 \\ 1 &>2 \end{matrix}\right.$
- Stabilire le soluzioni del sistema: $\displaystyle \left\{\begin{matrix} 4x-5 &>2x+6 \\ x^{2}+1 &>-3 \\ 2x &>1 \end{matrix}\right.$
- Stabilire le soluzioni del sistema: $\displaystyle \left\{\begin{matrix} 4x &>0 \\ x^{2}+4 &>-2\sqrt{5} \\ x &>1 \end{matrix}\right.$
- Stabilisci senza fare il calcolo che: $\displaystyle 10000^{5}<5^{10000}$
Parte IV
- Calcolare la distanza tra i punti P(-21,0), P(10,0).
- Le rette y = 4x – 1, y = 4x – 2 sono parallele?
- Il punto P(1,0) appartiene alla retta d’equazione: $\displaystyle y=x+1$ ?
- Il punto P(0,1) appartiene alla curva d’equazione: $\displaystyle y=x^{2}+2$ ?
- Il punto P(1,-7) appartiene alla curva d’equazione: $\displaystyle y=\sqrt{x^{2}+3x+7}$ ?
- Le rette y = 3x – 1, y = – 3x sono perpendicolari?
- La circonferenza d’equazione $\displaystyle x^{2}+y^{2}-4=0$ ha il centro nel punto O(0,0)?
- Se due circonferenze hanno tre punti in comune allora coincidono?
- Il punto P(2,3) appartiene alla retta x = 2?
- Il punto P(-7, 5) appartiene alla retta y = 4?
- Il punto P(1,1) appartiene alla circonferenza $\displaystyle x^{2}+y^{2}=2$ ?
- L’equazione y = – 1 si può riguardare come una funzione costante?
- L’uguaglianza $\displaystyle senx=-200$ è verificata per qualche valore di x ?
- La disuglaglianza $\displaystyle 3^{x}>-1$ è verificata per ogni valore di x ?
- L’uguaglianza $\displaystyle tanx=-100000$ è verificata per qualche valore di x ?
- Il fascio di rette di equazione $x+y+k(x-y)=0$ può avere centro nel punto (2, -4)?
- ll fascio di rette di equazione $2x+y+k(3x-y)=0$ ha centro nell’origine O per qualsiasi valore di k?
Parte V
- Risolvere la disequazione $\displaystyle senx>-1$.
- Risolvere la disequazione $\displaystyle cosx<-4$ .
- Risolvere la disequazione: $\displaystyle cos^{2}x+sen^{2}x-3>0$
- $\displaystyle sen(1)>\frac{1}{2}$
- L’uguaglianza x = -1 esprime in un piano Oxy l’insieme dei punti aventi ascissa uguale a -1?
- In un triangolo rettangolo di ipotenusa 1 e con un angolo di 30 gradi, il lato opposto all’angolo di 30 gradi è ½ ?
- L’uguaglianza $\displaystyle log\left ( 1-x \right )=1$ ha significato per x > 1 ?
- L’equazione $\displaystyle log_{x}(4x-4)=2$ ammette per soluzione x = 2?
- L’equazione $\displaystyle log_{x}(16)=4$ ammette per soluzione x = -2 e x = 2?
- La funzione $\displaystyle y=x^{2}-2x+1$ è pari?
- La funzione $\displaystyle y=x^{2}$ è iniettiva?
- La funzione $\displaystyle y=x+1$ è biettiva?
- La funzione $\displaystyle y=x$ è strettamente decrescente?
- Il dominio della funzione $\displaystyle y=\frac{3}{x^{2}+1}$ è l’insieme $\displaystyle R-\left \{ +1, -1 \right \}$ ?
- Stabilire il dominio della funzione \[y=\frac{\sqrt{3}}{x^{2}+1}+\frac{ln(x^{2}+4)}{x}\]
- Stabilire il dominio della funzione \[y=\frac{arctan\sqrt{x^{2}+1}}{ln(x^{2}+1)}-\frac{3^{\frac{1}{x}}}{e^{x^{2}+3}+5}\].
- Stabilire il codominio della funzione \[y=\frac{x}{x-1}\].
- La funzione $\displaystyle f(x)=x^{13}+1$ , a coefficienti reali, ammette come radice -1?
Parte VI
- La curva d’equazione $\displaystyle y=e^{x}$ passa per il punto P(1,-1) ?
- La curva d’equazione $\displaystyle y=lnx$ passa per il punto P(-1,1) ?
- La curva d’equazione $\displaystyle y=\left ( x^{2}+1 \right )^{2}$ interseca la retta y = – 2?
- La curva d’equazione $\displaystyle y=e^{x}+1$ interseca la retta x = – 7?
- La curva d’equazione $\displaystyle y=lnx$ interseca la retta x = -1? e la retta y = -7?
- La curva d’equazione $\displaystyle y=x^{2}+1$ ammette la retta y = 1 come tangente?
- La curva d’equazione $\displaystyle y=\frac{\sqrt{x}}{x^{2}+1}$ interseca la retta x = -1? e x = 1?
- La curva d’equazione $\displaystyle y=e^{x}$ interseca la retta y = x ?
- Le curve $\displaystyle y=e^{x}$ e $\displaystyle y=-x^{2}$ hanno punti in comune?
- Le curve $\displaystyle y=log_{\frac{1}{2}}x$ e $\displaystyle y=x^{2}$ hanno punti in comune?
- Le curve $\displaystyle y=senx,\, \, y=4$ hanno punti in comune?
- Le curve $\displaystyle y=senx$ e y = 100000 hanno punti in comune?
- Le curve $\displaystyle y=tanx$ e y = – 1000 hanno punti in comune?
- Verificare che: $\displaystyle \lim_{x\rightarrow +1 }\left ( x+1 \right )=2$
- Calcolare il limite $\displaystyle \lim_{x\rightarrow +\infty }\frac{\sqrt{3}}{x^{2}+1}$ .
- Calcolare il limite $\displaystyle \lim_{x\rightarrow +1 }\frac{x\sqrt{3}}{\left ( x-1 \right )^{2}}$ .
- Calcolare il limite $\displaystyle \lim_{x\rightarrow +\infty }\frac{\sqrt{x^{2}+10000000000000}}{x}$
- Calcolare il limite $\displaystyle \lim_{x\rightarrow +3 }\frac{x-3}{x-3}$
- Calcolare il limite $\displaystyle \lim_{x\rightarrow +1000000 }\frac{x^{2}+4}{x^{2}+4}$
- Calcolare il limite $\displaystyle \lim_{x\rightarrow 0^{+} }e^{\frac{1}{x}}$
Parte VII
- Calcolare il condominio della funzione $\displaystyle x^{2}y-1=0$ .
- Stabilire gli asintoti della funzione $\displaystyle y=\frac{1}{x^{2}-1}$ .
- La funzione $\displaystyle y=x^{3}+2x+1$ ammette nell’intervallo [1, -1] massimo e minimo assoluto?
- a funzione $\displaystyle y=x^{3}+2x+1$ ammette nell’intervallo [-1, 0] uno zero?
- Stabilire la positività della funzione $\displaystyle y=-3\left ( x^{2}+2 \right )$ .
- La funzione $\displaystyle y=x^{3}+1$ è strettamente crescente?
- Calcolare la derivata della funzione: $\displaystyle f(x)=e^{x+1}$ .
- Sia y = f(x) una funzione definita in D – {c} e tale che y’(c) = 0. Stabilire se la funzione in c può ammettere un massimo relativo?
- Stabilire il massimo della funzione $\displaystyle y=x^{2}+1$ .
- Stabilire gli estremi superiore ed inferiore della funzione $\displaystyle y=x^{3}+1$ .
- Stabilire gli zeri della funzione $\displaystyle y=x^{3}+1$ .
- La funzione $\displaystyle y=-3\left ( x^{2} +2x^{4} \right )+1$ è simmetrica rispetto all’asse y?
- Stabilire il flesso della funzione $\displaystyle y=x^{3}+5$ .
- Una funzione y = f(x) ha per derivata . Allora y ha concavità sempre rivolta nella direzione positiva dell’asse y?
- Verificare se la funzione $\displaystyle y=\left | x-1 \right |$ soddisfa al teorema di Rolle nell’intervallo [0, 2].
Parte VII
- Verificare se la funzione y = – 4 verifica il teorema di Rolle nell’intervallo [ -1, 1].
- Verificare se la funzione $\displaystyle y=\sqrt{x-1}$ verifica il teorema di Rolle nell’intervallo [-1, 0] .
- Verificare se la funzione y = x verifica il teorema di Lagrange nell’intervallo [0,1] .
- Il differenziale della funzione $\displaystyle y=3x^{2}$ è $\displaystyle dy=6xdx?$
- L’integrale di $\displaystyle \int 2xdx=\int xdx+\int xdx\, \, ?$ ?
- Calcolare l’integrale $\displaystyle \int\frac{2x}{1+x^{2}}dx$ .
- Calcolare l’integrale$\displaystyle \int_{3}^{3}\frac{2x+3}{x^{2}+1}dx$ .
- Se la somma di due numeri è costante allora il loro prodotto è massimo se i numeri sono uguali?
- La funzione $\displaystyle y=\frac{x}{x}$ ha per dominio tutto R?
- Stabilire il grafico della funzione $\displaystyle y=\frac{x-1}{x-1}$
- La funzione $\displaystyle y=\frac{x+1}{x+1}$ ammette nel punto x = -1 una discontinuità eliminabile?
- Sapendo che \[\int_{-\infty }^{+\infty }e^{-x^{2}}dx=\sqrt{\pi }\] calcolare la derivata della funzione $\displaystyle e^{h(x)}$ ove h(x) è l’integrale a primo membro dell’uguaglianza su indicata.
- Calcolare la primitiva di $\displaystyle y=e^{ln\, 2}$ che nel punto 1 assume valore 2.
- Calcolare il seguente integrale: \[\int sen^{4}x\, cosx\, dx\] Sostituendo a 4 il numero 1001 calcolare l’integrale in 4 secondi … ; poi scambia gli esponenti delle due funzioni e stabilisci se l’integrale non cambia!
- Calcolare i seguenti integrali (per ognuno hai a disposizione max 5 secondi): \[\int \frac{1}{xlnx},\int \frac{1}{xln^{2}x},\int \frac{1}{x(1+lnx)},\int \frac{1}{x(1+ln^{2}x)}\]
Se non ci riesci in meno di 30 secondi vedi il video
- Calcolare i seguenti integrali \[\int log_{2}2^{x}\, dx,\int x^{\pi }dx,\int \left ( \int dx \right )dx\]
- Calcolare il seguente integrale: \[ \int \frac{x^{\frac{\sqrt{x}}{ln\, x}}}{\sqrt{x}}dx\]
- Calcolare i seguenti integrali
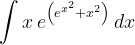 ,
,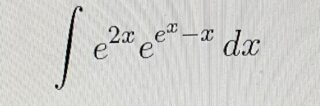
- Calcolare i seguenti integrali: $ \int e^{ln\, x+\: x^{2}}dx$, $ \int e^{ln\, x+\: 7\pi }dx$
