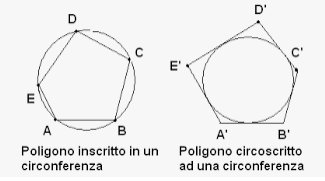
Quando un poligono è inscritto in una circonferenza, il centro della circonferenza coincide con il circocentro del poligono (punto d’incontro degli assi del poligono).
Un poligono è circoscritto in una circonferenza quando tutti i suoi lati sono tangenti alla circonferenza.
Quando un poligono è circoscritto in una circonferenza, il centro della circonferenza coincide con l’incentro del poligono (punto d’incontro delle bisettrici degli angoli del poligono).
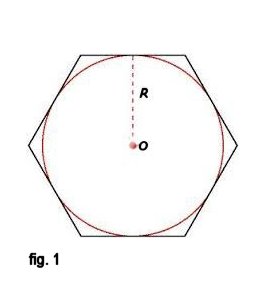
In un poligono regolare circocentro e incentro coincidono (fig. 3) e ogni poligono regolare ammette una circonferenza inscritta e circoscritta. Il raggio R (fig. 1) della circonferenza inscritta è detto apotema del poligono e rappresenta la distanza di ogni lato dal centro.
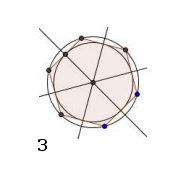
Altri poligoni:
- I triangoli sono sempre sia inscrivibili (circocentro) e circoscrivibili (incentro).
- I rettangoli sono sempre inscrivibili (circocentro) ma non circoscrivibili.
- I rombi sono sempre circoscrivibili (incentro) ma non inscrivibili.
- I trapezi isosceli sono sempre inscrivibili (circocentro) in una circonferenza.
Area di un triangolo
L’area S di un triangolo ABC inscritto in una circonferenza, cioè con i vertici sulla circonferenza, di raggio R (fig. 1) si può calcolare con la seguente formula \[S=\frac{1}{2}a\cdot b\cdot sen\, \theta\]
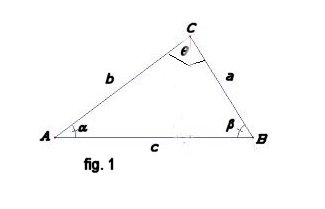
Formula di Erone
L’area S di un triangolo (fig. 1) si può calcolare con la formula di Erone \[S=\sqrt{p\left ( p-a \right )\left ( p-b \right )\left ( p-c \right )}\] con p semiperimetro.
Area di un triangolo inscritto in una circonferenza
L’area S di un triangolo inscritto in una circonferenza di raggio R (fig. 1) si può calcolare con la seguente formula \[S=\frac{a\cdot b\cdot c}{4R}\]
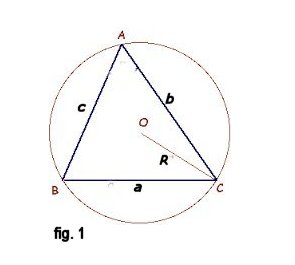
Area di un triangolo circoscritto ad una circonferenza
L’area S di un triangolo circoscritto ad una circonferenza di raggio r e semiperimetro p (fig. 2) si può calcolare con la seguente formula \[S=r\cdot p=\frac{r}{2}\left ( a+b+c \right )\]
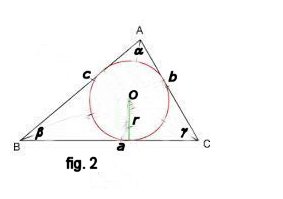
Area e perimetro dei poligoni regolari inscritti e circoscritti ad una circonferenza
a) L’area S e il perimetro P del poligono di n lati circoscritto alla circonferenza di raggio R (fig. 1) si determinano con le seguenti formule rispettivamente: \[\begin{matrix} S&=\frac{1}{2}\cdot n\cdot R^{2}\cdot sen\left ( \frac{360^{\circ}}{n} \right ) \\ & \\ P&=2\cdot n\cdot R\cdot sen\left ( \frac{180^{\circ}}{n} \right ) \end{matrix}\]

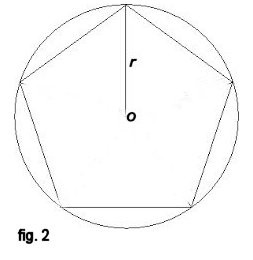
b) L’area S e il perimetro P del poligono di n lati inscritto nella circonferenza di raggio r (fig. 2) si determinano con le seguenti formule rispettivamente: \[\begin{matrix} S&= n\cdot r^{2}\cdot tan\left ( \frac{180^{\circ}}{n} \right ) \\ & \\ P&=2\cdot n\cdot r\cdot tan\left ( \frac{180^{\circ}}{n} \right ) \end{matrix}\]

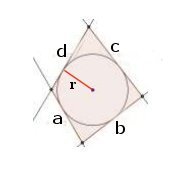
Area di un poligono non regolare circoscritto ad una circonferenza
\[A=p\times r\]
$\displaystyle p=\frac{a+b+c+d}{2}$ è il semiperimetro del poligono e r il raggio della cinconferenza inscritta nel poligono.