\[d=\frac{m}{V}\]
Nel sistema internazionale S. I. la densità si misura in kg/m3
Tabella della densità di alcune sostanze.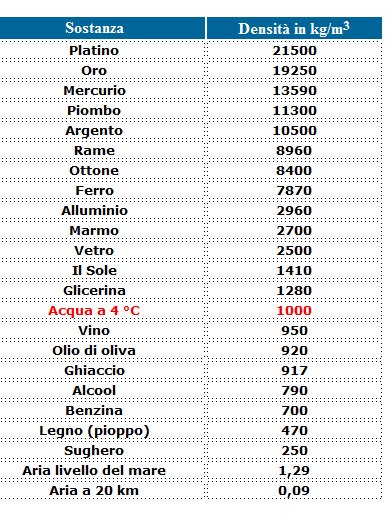
Identificando la massa di una sostanza con il suo peso la densità si identifica con il peso specifico (ps) e la formula precedente si può scrivere anche nella forma:
\[p_{s}=\frac{P}{V}\]
essendo P il peso della sostanza e V il suo volume. Se il peso è espresso in chilogrammi il volume deve essere espresso in decimetri cubi, mentre se il peso è espresso in tonnellate il volume deve essere espresso in metri cubi, mentre se il volume è espresso in centimetri cubi il peso è espresso in grammi.
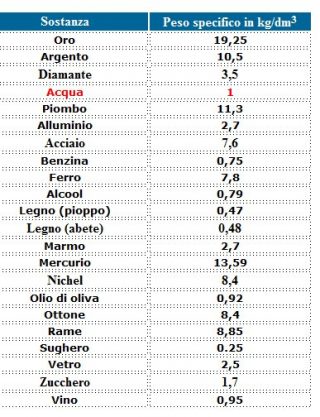
Tabella del peso specifico di alcune sostanze.
Formule inverse:
\[V=\frac{P}{p_{s}},\, \, \, \, P=V\cdot p_{s}\]
A rigore invece il peso specifico ps e la densità d sono collegate dalla seguente relazione:
\[p_{s}=d\cdot g\]
ove g è l’accelerazione gravitazionale terrestre ( g è circa uguale a 9,8 m/sec2 ).
Ricordiamo che il peso specifico è definito a rigore dalla seguente relazione:
\[p_{s}=\frac{P}{V}=\frac{mg}{V}\]
Ricordiamo però che il peso non è la massa di un corpo, anche se i due termini si confondono tra loro nel linguaggio comune. A rigore in fisica la massa è una grandezza fondamentale della fisica e il peso è una grandezza derivata, precisamente il peso è una forza, ovvero quella forza che si ottiene moltiplicando la massa per l’accelerazione di gravità g = 9,8 m/s^2. Avere ad esempio una massa di 70 kg significa avere un peso di 686 N (Newton, unità di misura della forza)
Esempio 1.1.- Calcolare il peso di un cubo di ferro di lato 15 dm.
Risoluzione
Applichiamo la formula inversa:
P = ps ´ V = 0,7 kg/dm3 ´ (15 dm)3 = 2362,5 kg
Esempio 1.2.- Calcolare il peso di un tronco di legno di abete lungo 7,8 metri e avente come raggio di base 25 cm
Risoluzione
La risoluzione di questo esercizio permette di sapere il peso di un tronco di legno di data lunghezza e dato raggio di base sapendo il peso specifico del legno in questione.
Nel nostro esempio si tratta di un tronco di legno di abete con peso specifico 0,48 kg/dm3. Per calcolare il peso del tronco di legno in questione cominciamo a calcolare il suo volume, ossia il volume di un cilindro (figura a) cui si può assimilare il pezzo di legno.
Il volume del cilindro è:
V = Ab ´ h = pR2 ´ h = p(25 cm)2 ´ 7,8 m = p(2,5 dm)2 ´ 78 dm = p ´ 6,25 dm2 ´ 78 dm =
= p ´ 6,25 dm2 ´ 78 dm = p ´ 487,5 dm3 = 3,14 ´ 487,5 dm3 » 1530,75 dm3
Pertanto conoscendo il peso specifico dell’abete si può calcolare il peso del tronco di legno senza metterlo su una bilancia! Si ha:
P = ps ´ V = 0,48 kg/dm3 ´ = 1530,75 dm3 = 734,76 kg.
Esempio 1.3.- Calcolare il peso di un tronco di legno di forma cilindrica e di cui non si conosce il peso specifico sapendo che la lunghezza del tronco è 14 m e avente come raggio di base 28 cm.
Risoluzione
Vi sono due possibilità:
- Sistemare il tronco di 14 m su di una bilancia e pesarlo!
- Applicare la formula P = ps ´ V calcolando prima il peso specifico del tronco.
Noi vogliamo svolgere il problema con il metodo esposto al punto 2).
Tagliamo una striscia del tronco di altezza 10 cm e pesiamola con una bilancia e immaginiamo di ottenere 3,7 kg.
Determiniamo poi il volume del cilindro di legno.
Dato che il volume del cilindro si determina con la formula V = Ab ´ h = pR2 ´ h si ha:
V = 3,14 ´ (24 cm )2 ´ 10cm = 3,14 ´ (2,4 dm )2 ´ 1 dm = 18,086 dm3
Pertanto il peso specifico del legno in questione è
ps = P/V = 3,5 kg / 18,086 dm3 = 0,19 kg/dm3
ne consegue che il peso di tutto il tronco si può ottenere così:
P = ps ´ V = 0,19 kg/dm3 ´ [3,14 ´ (2,4 dm )2 ´ 14 m ] =
= 0,19 kg/dm3 ´ [3,14 ´ (2,4 dm )2 ´ 140 dm ] =
= 0,19 kg/dm3 ´ 2532,09 dm3 = 481 kg

Scaffalatura legna da ardere per stufa e camini
Esempio 1.4.- Calcolare il peso di un oggetto grande omogeneo formato da una sola sostanza di cui non si conosce il peso specifico e il volume V0 è noto.
Risoluzione
Vi sono due possibilità:
- Sistemare l’oggetto su di una bilancia e pesarlo!
- Applicare la formula P = ps ´ V calcolando prima il peso specifico del tronco.
Noi vogliamo svolgere il problema con il metodo esposto al punto 2) per mostrare come si può calcolare praticamente il peso specifico di una sostanza più pesante dell’acqua. Supponiamo anche che si possa staccare (o tagliare) un pezzettino della sostanza di cui è fatto l’oggetto.
Tagliamo una pezzettino della sostanza di cui è fatto l’oggetto e immergiamo il pezzo così ottenuto in una vasca d’acqua sufficientemente grande e di cui sappiamo il volume (in litri) d’acqua che contiene. Per semplicità si può considerare una vasca a forma di parallelepipedo di date dimensioni e contenente all’interno una scala graduata che esprime il numero di litri d’acqua contenuti in base all’altezza raggiunta dall’acqua.
Dopo aver immerso il pezzettino nella vasca si noterà un certo aumento di volume, ossia l’acqua si alzerà di livello, misurabile in base alla scala graduata. Immaginiamo dunque che l’immersione completa del cilindro in acqua abbia fatto alzare il livello di due tacche corrispondenti ad un aumento di 3,5 litri.
E’ evidente che il pezzettino immerso nell’acqua ha un volume proprio pari 3,5 litri, che espresso in decimetri cubici è 3,5 dm3. Pesiamo poi il pezzettino con una normale bilancia e supponiamo che il peso del pezzettino sia di 6,8 kg
Pertanto il peso specifico si può calcolare nel seguente modo
ps = P/V = 6,8 kg /3,5 dm3 = 1,94kg / dm3
ne consegue
P = ps ´ V0 = 1,94 kg / dm3 ´ V0 = 1,94V0 kg
Ad esempio se V0 = 8,546 m3 = 8,546 dm3 si ha:
P = 1,94 ´ 8546 kg = 16237,4 kg
