Argomenti propedeutici:
- Disequazioni in una variabile
- Geometria analitica
Esempio 1. Risolvere la disequazione \[x+y-3>0\]
Risoluzione
Disegnare nel piano cartesiano Oxy la retta d’equazione \[y=-x+3\] determinando due suoi punti, ad esempio i punti T(0,3) e P(3,0), che dividerà il piano in due semipiani. Le soluzioni della disequazione assegnata sono i punti (x, y) del piano situati al di sopra della retta y = – x + 3, (parte evidenziata in giallo) e aventi per ascissa un qualsiasi numero reale. Notiamo che i punti situati sulla retta non sono soluzioni della disequazione assegnata e per evidenziarlo la retta si disegna tratteggiata.
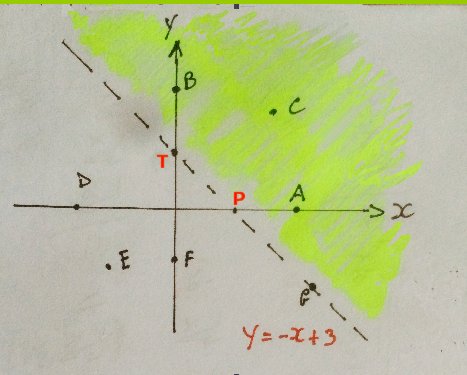
Ad esempio i punti A, B, C sono soluzioni della disequazione, mentre non lo sono i punti D, E, F, G, O, T e P.
Esempio 2. Risolvere la disequazione: \[2x-3y-6\geq 0\]
Risoluzione
Dalla disequazione assegnata si ricava la seguente retta: \[2x-3y-6>0\rightarrow 3y<2x-6\rightarrow y=\frac{2}{3}x-2\]
Quindi diisegnata tale retta nel piano cartesiano Oxy si vede che le soluzioni della disequazione sono…
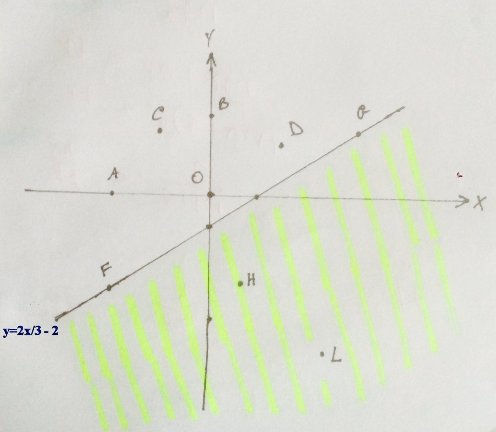
Ad esempio i punti A, B, C, O, D non sono soluzioni della disequazione, mentre lo sono i punti F, G, H, L.
Esempio 3. Risolvere la disequazione in due variabili: \[x^{2}-y^{2}-4\geq 0\]
Esempio 4. Risolvere la disequazione in due variabili \[6x^{2}+2y-4> 0\]
Esempio 5. Risolvere la disequazione in due variabili: \[x^{2}-y^{2}> 0\]
Suggerimento
La disequazione assegnata si può scrivere nel seguente modo \[x^{2}-y^{2}>0\Rightarrow \left ( x+y \right )\left ( x-y \right )>0\]
e quindi, risolvendo come una disequazione prodotto, si ha:…
Esempio 6. Risolvere la disequazione in due variabili: \[\frac{x}{x}>-1\]
Esempio 7. Risolvere la disequazione in due variabili: \[\frac{x}{y}\leq -1\]
Esempio 8. Risolvere la disequazione in due variabili \[\frac{x-y}{x+y}>0\]
Esempio 9. Risolvere la disequazione in due variabili: \[\frac{x^{2}-y}{y-1}>0\]
Esempio 10. Risolvere il sistema in due variabili: \[\left\{\begin{matrix} y-x+1 &>0 \\ y+x^{2} & >0\\ y+1&<0 \end{matrix}\right.\]
Esempio 11. Risolvere la disequazione in due variabili \[y-x^{3}-1>0\]
Esempio 12. Risolvere la disequazione in due variabili: \[\frac{e^{x}-y}{y+x+2}\geq 0\]
Esempio 13. Risolvere la disequazione in due variabili: \[\frac{y^{2}+x^{2}-1}{\sqrt{x+y}}> 0\]
Esempio 14. Risolvere il sistema in due variabili: \[\left\{\begin{matrix} \frac{x^{2}}{9}+\frac{y^{2}}{4} &<1 \\ \frac{x}{3}+\frac{y}{2} & \geq 1\\ y-3^{x}&<0 \end{matrix}\right.\]
Esempio 15. Risolvere la disequazione: \[x+\sqrt{x^{2}-y^{2}}>0\]
Esempio 16. Risolvere il seguente sistema \[\left\{\begin{matrix} x^{2}+y^{2}-1 & \leq 0\\ y+x-1 & \leq 0\\ 2y &\geq 0 \end{matrix}\right.\]
Vedi il mio video nel mio canale Youtube se non sai risolvere l’esercizio.
