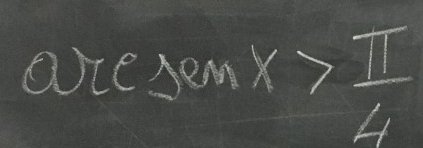Disequazioni con le funzioni goniometriche inverse
La disequazione elementare:\[1)\, \, arcsen\, x>m\]
con \[m\in \left ( -\frac{\pi }{2},\frac{\pi }{2} \right )\] tenuto conto che l’arcoseno è una funzione crescente, è risolubile nel seguente modo:
\[arcsen\, x>m\Rightarrow arcsen\, x>arcsen(sen\, m)\Rightarrow sen\, m<x\leq 1\]
La (1) è:
- impossibile se \[m\geq \frac{\pi }{2}\]
- verificata per \[\forall x\in \left [ -1,1 \right ]\, se\, m< -\frac{\pi }{2}\]
- e verificata per \[\forall x\in (-1,1],\, se\, m= -\frac{\pi }{2}\]
Notiamo esplicitamente che la soluzione \[x\in \left [ -1,1 \right ]\] ..
Esempio 1.- Risolvere la disequazione \[arcsen\, x>\frac{\pi }{4}\]
Risoluzione
Risolviamo preliminarmente l’equazione \[arcsen\, x=\frac{\pi }{4}\] e otteniamo \[x=\frac{\sqrt{2}}{2}\] Ne consegue l’identità \[arcsen\frac{\sqrt{2}}{2}=\frac{\pi }{4}\] e che utilizziamo per risolvere la disequazione data.
Si ha: \[arcsen\, x>arcsen\frac{\sqrt{2}}{2}\Rightarrow\frac{\sqrt{2}}{2} <x\leq 1\]
Esempio 2.- Risolvere la disequazione \[arccos\, x>\frac{\pi }{3}\]
Esempio 3.- Risolvere la disequazione \[arcctan\, x>\frac{\pi }{4}\]
Esempio 4.- Risolvere la disequazione \[arccot\, x>\frac{\pi }{6}\]
Esempio 5.- Risolvere le disequazioni \[arctan\, x>0\] \[arctan\, x>-\frac{\pi }{4}\] \[arctan\, x>-7,\, arctan\, x<-8,\, arctan\, x>8,\, arctan\, x<199\]
Esempio 6.- Risolvere la disequazione \[arctan^{2}x-3arctan\, x+2< 0\] \[arcsen^{2}(2x)-arcsen(2x)-2>0\] \[arcsen(2x+1)>arcsen(2x-3)\]
Esempio 7.- Risolvere la disequazione \[2arctanx\leq arcsen(2x)\].
Se non sai risolvere la disequazione prova a vedere il mio video sul mio canale Youtube
Molti altri esercizi svolti li puoi trovare nel mio libro Disequazioni