Esempio 1.1.- Estrazione di una carta, lancio di un dado, estrazione di una pallina. Qual è la probabilità che lanciando un dado non truccato esca un numero dispari? qual è quella che esca un multiplo di 3? Qual è quella che esce un numero maggiore di 9? Qual è quella che esca un numero maggiore di zero?
Esempio 1.2.- Qual è la probabilità che scegliendo una carta da un mazzo di 52 carte francesi esca l’asso di cuori? Qual è la probabilità che esca un asso?
Esempio 1.3.- Estraendo una carta da un mazzo di 52 carte francesi qual è la probabilità che non sia una carta di quadri?
Esempio 1.4.- Un’urna contenente 7 palline rosse, 23 nere e e 14 gialle. Qual è la probabilità che estraendo una pallina dall’urna sia nera? Qual è la probabilità che sia nera o gialla? Qual è la probabilità che non sia nera? Qual è la probabilità che sia o nera o gialla o rossa?
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube
Esempio 2.1.- Estrazione di due carte, lancio di due dadi, estrazione di due palline. Qual è la probabilità che lanciando due dadi non truccati esca almeno un cinque? Qual è la probabilità che esca un numero superiore a 12? E qual è la probabilità che esca un nove?
Esempio 2.2.- Lanciando due volte un dado determinare la probabilità che esca due volte il 6. Qual è invece la probabilità che esca 6 al primo lancio e 4 al secondo? Qual è la probabilità che 6 al primo lancio e un numero diverso da 4 al secondo?
E se si volesse la probabilità che non esca il 6 né al primo lancio né al secondo?
Esempio 2.3.- Lanciando successivamente due monete ben equilibrate qual è la probabilità che escano due teste?
Esempio 2.4.- Estraendo successivamente due carte da un mazzo di 52 carte francesi, Stabilire la probabilità che la prima carta sia un asso e la seconda una figura. Qual è la probabilità che siano due carte di quadri?
Primo caso: Rimettendo ogni volta la carta nel mazzo
Secondo caso: Sena rimettere la carta estratta nel mazzo
Esempio 2.5.- Un’urna contiene 50 palline rosse e 150 di colore verde. Procediamo a due estrazioni nel seguente modo: se viene estratta una pallina verde la rimettiamo nell’urna, se invece viene estratta una pallina rossa la togliamo e inseriamo una pallina verde nell’urna. Calcolare la probabilità di avere nell’urna 49 palline rosse e 151 verde dopo due estrazioni.
Risoluzione
Dopo due estrazioni si possono avere 49 palline rosse e 151 di colore verde se si verificano i seguenti due eventi incompatibili:
E ={ estrazione di una pallina verde seguita da una pallina rossa}
H = { estrazione di una pallina rossa seguita da una verde}
La probabilità dell’eventi E e H, per il teorema della probabilità composta, sono rispettivamenteè p(E) = 0,375, p(H) = 0,18875.
Quindi per il teorema della probabilità totale si ha che p = p(E) + p (H)
Esempio 2.6.- Un’urna contiene 12 palline bianche. Qual è il numero minimo di palline nere da aggiungere affinché estraendo due palline contemporaneamente la probabilità che esse siano una bianca e una nera sia 1/11?
Risoluzione ragionata
Indichiamo con x il numero delle palline nere da aggiungere calcoliamo le probabilità seguenti:
p(NB) = probabilità di estrarre la prima pallina nera (N) e la seconda bianca (B) = …
p(BN) = probabilità di estrarre la prima pallina bianca e la seconda nera = …
Quindi si sommano tale probabilità e si uguagliano ad 1/11, risolta l’equazione si ha che x = 2
Esempio 3.1- Altri problemi. Estraendo contemporaneamente 3 carte dalle 13 di cuori di un mazzo di carte francesi, determinare la probabilità che siano due di valore compreso tra 1 (asso) e il 6 e l’altra di valore maggiore o uguale a 7.
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube
Esempio 3.2.- Lanciando tre dadi stabilire se è più probabile che esca nove o dieci.
Non sai risolvere l’esercizio? Allora vedi il mio video su Youtube
Esempio 3.3.- Lanciando successivamente tre monete ben equilibrate qual è la probabilità che escano almeno due teste?
Esempio 3.4.- Si lancia un dado truccato numerato da 1 a 6 con le seguenti probabilità:
P(1) = 5/16,
P(2) = P(3) = 1/16
P(4) = 1/4
P(5) = 3/16
P(6) = 1/8
Determinare la probabilità dell’evento E = ” Esce un multiplo di 3 oppure un numero minore o uguale di 2″
Esempio 4.1.- Probabilità condizionata.- Un’urna contiene p palline bianche e q rosse. Si estrae una pallina e, successivamente, senza rimettere la prima pallina nell’urna, se ne estrae una seconda. Se la prima pallina estratta è bianca, qual è la probabilità che anche la seconda sia bianca? [ (p – 1)/(p+q-1)]
Risolvere lo stesso esercizio stabiliendo la probabilità che entrambe le palline siano bianche senza sapere che la prima estratta sia bianca. [ p(p – 1)/(p+q)(p+q-1)]
Esempio 4.2.- A un esame di universitario si presentano sia studenti che hanno seguito il corso sia studenti che non l’hanno seguito. Secondo Il docente il 65% degli studenti ha seguito il corso. La probabilità che uno studente superi l’esame sapendo che ha seguito il corso è 0,75, mentre la probabilità che superi l’esame, sapendo che non ha seguito il corso, è 4 persone su 10, stabilire:
- Quali sono gli eventi descritti dal testo?
- Nel teso sono già espresse delle misure di probabilità. A quali eventi si riferiscono? Per ciascuno evento, scrivere la sua probabilità in rappresentazione decimale.
- Qual è la probabilità che uno studente superi l’esame?
- Qual è la probabilità che uno studente abbia seguito il corso sapendo che non ha superato l’esame?
- Qual è la probabilità che uno studente scelto a caso abbia superato l’esame o non abbia seguito il corso?
Risoluzione
Indichiamo con A e B i due eventi elementari:
A = { lo studente supera l’esame},
B = { lo studente ha seguito il corso};
con $\displaystyle \overline{B}$ l’evento contrario a B e con P(B) la probabilità dell’evento B e con $\displaystyle P\left (\overline{B} \right )$ la probabilità dell’evento contrario a B.
Dato che il docente ritiene che “il 65% degli studenti ha seguito il corso”, approssimando la probabilità con la frequenza relativa, si ha P(B) = 0.65 e applicando la formula della probabilità dell’evento contrario si ha:
\[P\left (\overline{B} \right )=1-P(B)=1-0,65=0,35\]
Inoltre $\displaystyle P\left ( A/B \right )=0,75\, \, \, \, \, \, P(A/\overline{B})=0,40$ , visto che sono assegnati dal testo.
A questo punto possiamo rispondere alla terza domanda,
Osserviamo che l’evento A si può riguardare come \[A=\left ( A\cap B \right )\cup \left ( A\cap \overline{B} \right )\]
e dunque la probabilità è \[P\left ( A \right )=P\left ( A\cap B \right )+P\left ( A\cap \overline{B} \right )=0,4875 + 0,1400 = 0,6275\]
ossia 0,6275 è la probabilità che lo studente superi l’esame.
Quarta domanda. Mentre $\displaystyle P\left ( B/A \right )$ , ovvero la probabilità che lo studenti abbia seguito il corso ammesso che superi l’esame è: \[P\left ( B/A \right )=\frac{P\left ( A\cap B \right )}{P(B)}=\frac{0,4875}{0,65}=0,7769\]
Osservazione
\[P(A\cap B)=P(A/B)\cdot P(B)=0,75\cdot 0,65=0,4875\]
\[P(A\cap \overline{B})=P(A/\overline{B})\cdot P(\overline{B})=0,40\cdot 0,35=0,1400\]
Esempio 4.3.1- Formula di disintegrazione.- Da una un’urna contenente 9 palline di cui 5 nere e 4 bianche se ne estraggono a caso due consecutivamente, senza reimmissione della prima pallina estratta. Stabilire la probabilità che la prima pallina estratta sia bianca e che la seconda sia nera.
Esempio 4.3.2.- Tre urne T, S e Z hanno la seguente composizione di palline:
T = { 7 bianche, 3 nere}, S= { 3 bianche, 5 nere}, Z= { 5 bianche, 2 nere}
tre Si sceglie a caso una delle tre urne e si estraggono a caso due palline, stabilire la probabilità: che siano entrambe bianche; due nere; almeno una bianca; almeno una nera.
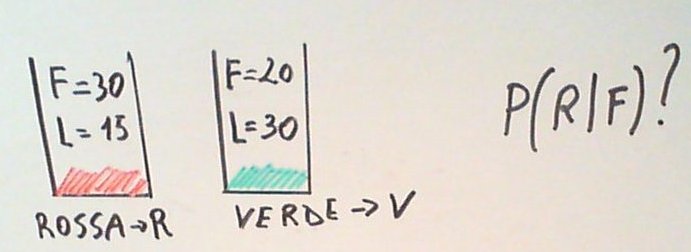
Esempio 5.1.- Teorema di Bayes.- Un negoziante vende cioccolatini di due tipi, Fondente e a Latte, e che tiene alla rinfusa in due scatole, scatola Rossa e scatola Bianca. Un bambino entra e chiede un cioccolatino, il negoziante prende a caso un cioccolatino da una delle due scatole e dà al bambino un cioccolatino Fondente. Sapendo che nella scatola Rossa ci sono 30 cioccolatini Fondente e 15 al Latte e che nella scatola Bianca ci sono 20 cioccolatini Fondente e 30 al Latte, calcolare la probabilità che il cioccolatino Fondente consegnato al bambino provenga dalla scatola Rossa.
Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.1.1.- Due urne.- Due urne T e S hanno la seguente composizione di palline:
T = { 8 bianche, 3 nere }, S = { 6 bianche, 12 nere }
Si estrae a caso una pallina da una delle due urne e si constata che è nera. Stabilire la probabilità che provenga dall’urna T
Esempio 5.1.2.- Tre urne.- Tre urne T, S e Z hanno la seguente composizione di palline:
T = { 7 bianche, 3 nere}, S= { 3 bianche, 5 nere}, Z= { 5 bianche, 2 nere}
Se si estraggono due palline bianche qual è la probabilità che provengano dall’urna T? E se si estraggono due nere qual è la probabilità che provengano dall’urna S? E se si estraggono due palline di colore diverso qual è la probabilità che provengano dall’urna Z?
Esempio 5.1.3.- Da un’urna contenente p palline rosse e q nere, si estrae
Esempio 5.4.1.- Pezzi difettosi. In una fabbrica vi sono due macchine, A e B, che producono lo stesso prodotto (pezzo), la macchina A ne produce il 70% e la B il 30%. I pezzi prodotti da A sono per il 60% di prima qualità, per il 25% di seconda qualità 8qualità media) e per il terzo di qualità scarsa (pezzi da scartare); per la macchina B, invece, i pezzi di prima qualità sono dell’80%, di seconda qualità invece sono il 15% e per il 5% di qualità scarsa. a) Calcolare le percentuali dei pezzi da scartare prodotti in fabbrica. b) Scegliendo a caso un pezzo tra quelli prodottti e osservato che sia di prima qualità, stabilire la probabilità che sia stato prodotto dalla macchina A.
Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.4.2.- Un commerciante ordina una paletta di lampadine, prima di venderle vuole fare un controllo di qualità. Sapendo che la probabilità che una lampadina, scelta a caso, sia buona è 0,7 e che sia 0,95 la probabilità che il controllo indichi come buona una lampadina che effettivamente lo è, e se infine è 0,05 la probabilità che il controllo indichi ocme buona una lampadina che non lo è, calcolare la probabilità che una lampadina, indicata come buona, sia invece fulminata (non buona).
Esempio 5.4.3.1- Tre macchine A, B e C, producono rispettivamente n,m, p articoli, di cui rispettivamente, h, k, t difettosi per un totale di n articoli. Tra gli articoli prodotti se ne sceglie uno a caso e si vede che è difettoso. Determinare la probabilità che sia stato prodotto dalla macchina A. Qual è invece la probabilità che sia stato prodotto dalla macchina B? Cakcolare poi la probabilità che il pezzo difettoso sia stato scelto dalla macchina A o C.
Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.4.3.2.- Tre macchinari producono gli stessi componenti elettronici. La produzione giornaliera è stata la seguente; 800 per il macchinario 1, 600 per il macchinario 2 e 400 per il macchinario 3. Sono stati individuati dei pezzi difettosi prodotti dai tre macchinari nelle seguenti percentuali; il 5% per il macchinario 1, il 4% per il macchinario 2 e 2% per il macchinario 3. I pezzi vengono confenzionati in scaltole contenenti ciascuna 100 pezzi provenienti da uno stesso macchinario. Calcolare la probabilità che, scegliendo a caso un pezzo, da una scatola, anch’essa scelta a caso, sia difettoso.
Esempio 5.4.3.3.- Un’azienda dispone di quattro macchine che sono in grado di filettare, per ogni ora, 1000 viti dello stesso tipo. In particolare
- la macchina 1 filetta 400 viti all’ora e la probabilità che si origini una vite difettosa è 0,08;
- la macchina 2 filetta 300 viti all’ora e la probabilità che si origini una vite difettosa è 0,06;
- la macchina 3 filetta 200 viti all’ora e la probabilità che si origini una vite difettosa è 0,05:
- la macchina 4 filetta 100 viti all’ora e la probabilità che si origini una vite difettosa è 0,04.
Alla fine di ogni ora si sceglie a caso una vite che risulta essere difettosa. Stabilire la probabilità che provenga dalla macchina 2
Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.5.- Un’atleta ha la proabilità delllo 0,7 di riposare bene la notte prima della gara. Se riposa bene, ha la probabilità di vincere la gara dello 0,6, se riposa male la probabilità di vincere è dello 0,25. Determinare la probabilità che l’atleta ha di vincere, di vincere se riposa male, di perdere se riposa bene.
Esempio 5.6.- Ad un esame per conseguire la patente di guida, un candidato è in possesso di una preparazione che gli consentirà di risolvere bene il 70% dei quiz. Per ogni quiz sono riportate cinque risposte fra le quali scegliere la risposta esatta. Se il candidato risponse esattamente ad un quiz, qual è la probabilità che abbia tirato ad indovinare? Qual è la probabilità per un altro candidato che è in grado di solvere soltanto il 10% dei quiz?
Se ora o in futuro questo sito ti è stato d’aiuto offrici un aiuto…
Esempio 5.7.- Antonio, Paolo e Riccardo possono diventare presidenti dell’Azienda Athena SpA con rispettive probabilità 1/2, 3/10 e 1/5. Nel caso fosse eletto Antonio la probabilità che Antonio incrementi il fatturato aziendale è dello 0,7 mentre per Paolo e Riccando la probabilità di incrementare il fatturato è rispettivamente dello 0,6 e 0,5. Dopo la scelta del presidente si nota che l’azienda subisce un aumento di fatturato. Stabilire la probabilità che sia stato eletto Antonio.
Esempio 5.8.1.- Sintomi e malattia, esami diagnostici. La probabilità che avendo il morbillo si sviluppi un eritema è del 96% e la probabilità che si sviluppi un eritema analogo in assenza di morbillo è dello 0,25%. Determinare la probabilità che un paziente abbia il morbillo se si constata che ha sviluppato un eritema, sapendo che l’incidenza nella popolazione è dello 0,45%.
A prima vista sembra di sì, ma… Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Avvertenza: Il teorema di Bayes è molto utile in campo medico e/o diagnostico e tutti dovrebbero padroneggiarlo bene. In questo campo sono note le frequenze degli eventi e le probabilità condizionate delle relazioni causali e, tali dati, sono utilizzati per calcolare la probabilità di un evento su un singolo soggetto, cioè calcolare la probabilità che una persona abbia una data malattia che presenta determinati sintomi, a partire dalla frequenza della malattia e dal grado di efficacia del test diagnostico.
Esempio 5.8.1.2.- E’ noto che per le donne sotto i 49 anni il tumore alla mammella si presenta nel 2,4% dei casi. Una signora con meno di 49 anni si sottopone alla mammografia e risulta positiva. Sapendo che il test della mammografia individua un vero positivo (test rivela un tumore e il tumore c’è realmente) nell’80% dei casi e che invece, se il tumore non c’è, il test risulta negativo in circa il 90% dei casi, stabilire se la signora deve preoccuparsi o meno.
A prima vista sembra di sì, ma… Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.8.1.3.- Una malattia colpisce 2 persona su 100. Un test dà esito positivo nel 98% dei casi su persone effettivamente malate e nello 0,5% dei casi su persone che invece stanno bene. Se una persona fa il test, che probabilità p ha di essere davvero malata se il test dà esito positivo?
Esempio 5.8.2.- In un paese si sa che una certa malattia M è endemica si sa che il 12% della popolazione si ammala della malattia M. Si dispone di un test per scoprire la malattia che nel 90% dei casi in cui si risulta positivi effettivamente si ha la malattia M e che nel 5% dei positivi invece si è sani. Si sceglie una persona a caso e si sottopone al test risultando positiva. Si stablisca la probablità di essere sana.
Esempio 5.8.3.- In un paese si diffonde un’epidemia (il Covid 19?) che colpisce il 3% della popolazione. Ben presto si trova un test che permette una diagnosi precoce del morbo. Il test ha l’1% di falsi positivi, cioè la probabiltà che il test sia positivo anche se non si ha il morbo è 0,01. Inoltre si ha lo 0,5% di falsi negativi. Se una persona si sottopone al Test quanto deve preoccuparsi se esce positivo? Quanto può stare tranquillo se esce negativo?
A prima vista sembra di sì, ma… Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.8.4.- Nel 2001 la Commissione Europea ha disposto l’esecuzione di un Test sulla popolazione bovina per individuare i capi infetti da Encefalopatia spongiforme bovina (BSE). Il test, come tutte le analisi cliniche, non è accurato al 199%. E’ stato determinato statisticamente che se la mucca è infetta, nel, nel 30% dei casi il test non lo rivela (si usa dire che il risultato è un falso negativo), mentre se la mucca è sana, nel 10% dei casi secondo il test risulta infetta (falso positivo). Supponendo che le mucche infette siano lo 0,0013%, qual è la probabilità che scegliendo a caso una mucca, questa risulti positiva al test?
Esempio 5.9.- Capelli biondi, rossi e neri.- In un paese scandinavo il 75% delle ragazze ha i capelli biondi, il 15% li ha rossi, il 10% mori. Risulta poi che ha gli occhi scuri il 12% delle bionde, il 24% delle rosse, il 52% delle more. Se la ragazza con cui ho fatto amicizia tramite Facebook mi fa sapere che ha gli occhi scuri, che probabilità c’è che sia bionda?
Esempio 5.10.1- Diventa come Sherlok Holmes! Il sigonr Giuseppe è accusato di un aver ucciso l’amante della moglie. Dopo le indagini e l’analisi delle prove il commissario stima che all’80% la probabilità che sia effettivamente colpevole. Successivametne perquisendo la casa del signor Giuseppe viene ritrovata una pistola, il commissario di polizia, in base alla propria esperienza, stima che un colpevole abbia una pistola con probabilità pari allo 0,95, e che un non colpevole ne possieda una con probabilità 0,1. Stabilire la probabilità che il signor Giuseppe sia colpevole dopo aver ritrovato la pistola.
Se non sai risolvere l’esercizio… prova a vedere il mio video su Youtube
Esempio 5.10.2- In un caso di omicidio ci sono due sospetti, Antonio e Giulio, considerati dalla polizia “ugualmente sospettati”. Sul luogo del delitto sono stati rinvenuti dei capelli non appartenenti alla vittima, e quindi appartenenti al colpevole. La prova del DNA sui capelli e sui due sospetti ha portato alla conclusione che il DNA ritrovato potrebbe appartenere all’70% ad Antonio e al 50% a Giulio. Qual è la probabilità che sia Antonio il colpevole alla luce dell’analisi del test sul DNA? E che sia Giulio?
Esempio 5.11.- Validità di un farmaco.- Per testare la validità di un farmaco lo si sperimenta su un campione di pazienti affetti da una certa malattia. Al 75% dei pazienti viene somministrato il farmaco, mentre al 25% viene somministrato un palcebo, ossia una sostanza priva di proprietà famacologiche (i pazienti sonon sono informati se stanno asummendo il farmaco o il placebo). Al termine del periodo di somministraizone sono guariti l’80% dei pazienti a cui è stato somminstrato il farmaco e il 10% dei pazienti a cui è stato somministrato il placebo. Se un poaziente è guarito, qual è la probabilità che gli sia stato somministrato il farmaco?
Esempio 5.12.- Docente o assistente?.- Uno studente universitario viene esaminato dal docente o dal suo assistente. La probabilità di essere esaminato dal docente è pari a 2/5. La probabilità di superare l’esame, se sostenuto con il docente, è 0,6 mentre con l’assistente è 0,8. Se lo studente ha superato l’esametne, qual è la probabilità che sia stato esamninato dal cocente?
Esempio 5.13.- Frecce e bersagli. Tre frecce vengono lanciiate contro un bersaglio da tre arcieri, A, B e C. Poichè i tre rcieri sono a diversa distanza dal bersaglio, si stima in 3/5 la probabilità dell’arciere A di fare centro, in 1/2 la probabilità di fare centro dell’arciere B e in 4/5 quella di fare centro dell’aricere C. Se una sola freccia raggiiunge il centro del bersaglio qual è la proabilità che sia stata lanciata dall’arciere A?
Esempio 5.14.- Tre macchine T, S e Z fabbricano viti dello stesso tipo. Le percentuali di viti difettose fabbricate dalle macchine T, S e Z è rispettivamente del ‘1%, del 2% e del 3%. Si mischiano in una scatola 120 viti, 20 fabbricate dalla macchina T, 40 fabbricate da S e 60 da Z. Scegliendo a caso una vite dalla scatola e visto che si tratta di una vite difettosa, stabilire la probabilità che sia stata fabbricata dalla macchina S. [Università di Alicante]
Esempio 5.15.- Un’azienda di trasporto pubblico gestisce tre linee di autobus di una grande città con il seguente orario di copertura: il 60% degli autobus dell’azienda coprono la linea numero 1, il 30% la linea numero 2 e il 10% la linea numero 3. Uno studio permette di sapere che la probabilità che un autobus abbia un guasto meccanido, quotidianamente, è è del 2% lungo la linea 1, del 4% lungo la linea 2 e del ‘1% lungo la linea 3. Calcolare la probabilità che in un giiorno un autobus abbia un guasto. Stabilire inoltre che se un autobus scelto a caso ha subito un guasto sia di quelli che percorrono la linea numero 1. [Salamanca]
Esempio 5.16.- La probabilità che un articolo per la casa sia fabbricatoo da una macchina S o T è rispettivametne dello 0,7 e 0,3. La macchina S produce articoli difettosi con probabilità pari a 0,02 e la T con probabilità pari a 0,06. Si sceglie a caso un articolo e si vede che è difettoso, stabilire la probabilità che sia stato prodotto dalla macchina S.
Esempio 5.17.- Su di uno scaffale di una biblioteca vi sono 60 libri di racconti scientifici e 20 di poesia. Antonio si reca in biblioteca sceglie un libro dallo scaffale e lo porta a casa. Successivamente Riccardo sceglie un altro libro dallo scaffale.. Stabilire la probabilità che il libro scelto da Riccardo sia di poesia. Inoltre, sapendo che Riccardo ha scelto un libro di racconti scientifici, stabilire la probabilità che il libro scelto da Antonio sia di poesia.
Esempio 5.18.- In un sistema di allarme, la probabilità che accada un incidente è dell0 0,1. Se accade l’incidente la probabilità che suoni l’allarme è 0,95 e la probabilità che l’allarme funzioni qualora non si avesse un incidente è delllo 0,03. Ammettiamo che sia scattato l’allarme stabililre la probabilità che si abbia avuto un incidente
Esempio 5.19.- Uno studente deve partecipare ad un concorso di prima mattina e dunque utilizza una sveglia per svegliarsi in tempo e partecipare al concorso. Sapendo che la sveglia lo svegli nell’80$ dei casi e sapendo che se lo studente sente la sveglia la probabilità di partecipare al concorso è 0,9 e in caso contrario dello 0,5, stabilire: se partecipa al concorso qual è la probabilità che ha sentito la sveglia? Se non partecipa al concorso, qual è la probabilità che non abbia sentito la sveglia?
Esempio 5.20.- Quattro urne T, S, Z e W contengono palline come di seguito indicato:
T = { 5 bianche, 4 nere, 1 gialla}, S = { 4 bianche, 3 nere, 6 gialle,}
Z = { 1 bianca, 2 nere, 2 gialle}, W = { 7 bianche, 3 nere, 0 gialle}
Scelta un’urna a caso, si estrae una biglia e questa viene reimmessa nell’urna a meno che non sia bianca. Il processo continua fino a quando non viene estratta una pallina bianca. Calcolare la probabilità che la pallina bianca sia stata estratta dall’urna T. Successivamente calcolare la probabilità che la pallina estratta sia stata estratta dall’urna W.
Esempio 5.21.- Una scatola contiene 9999 schede rosse e 1 scheda gialla, mentre una seconda scatola ne contiene 9999 gialle e 1 scheda rossa. Estraendo a caso da una delle scatole una scheda si riscontra che è rossa. Calcolare la probabilità che sia stata estratta dalla prima scatola.
Esempio 5.22.- Una televisione è costruita con componenti di buona qualità o con componenti di qualità mediocre. Nel primo caso la probabilità di funzionamento corretto per una durata di tempo t è di 0,95, mentre nel secondo caso è di 0,70. IL 40% delle televisioni contiene componenti di buona qualità. Se al collaudo una televisione funziona correttamente per il tempo t, calcolare la probabilità che essa sia costruita con componenti di buona qualità
Esempio 5.23.- Tra 100 persone vi sono 60 donne e 40 uomini. Sapendo che il 70% delle donne e il 40% degli uomini fumano, calcolare la probabilità che scelta a caso una persona che sta fumando questa sia donna.
Esempio 5.24.- Un’urna contiene 3 palline di cui 2 sono rosse e 1 gialla. Si sceglie una pallina a caso. Se essa è gialla la si rimette nell’urna aggiungendovi un’altra pallina gialla, mentre se essa è rossa la si ripone nell’urna aggiungendovi altre due palline rosse. Calcolare la probabilità che estraendo a caso una seconda pallina questa sia rossa. Sapendo poi che la seconda pallina estratta è rossa, calcolare la probabilità che anche la prima pallina estratta era rossa.
Esempio 5.25.- Un problema può essere risolto con un procedimento algebrico o con due distinti procedimenti geometrici. Se un alunnno sceglie la via algebrica ha la probabilità dell’80% di risolverlo correttamente, mentre se sceglie di procedere per via geometrica la probabilità di successo è del 50% e 40% rispettivametne. Se l’alunno risolve bene il problema, qual è la probabilità che egli abbia seguito il procedimento algebrico?
Esempio 5.26.- Alcuni amici organizzano una partita di tennis per il giorno seguente, sapendo che la probabilità che faccia bel tempo è dello 0,8. Si sa inoltre che se è bel tempo la probabilità che la partita abbia luogo è 0,9, mentre se è cattivo tempo la probabilità che si faccia la partita è 0,3. Se l’indomani la parita di tennis ha luogo, stabilire la probabilità che sia stata disputata con cattivo tempo.
