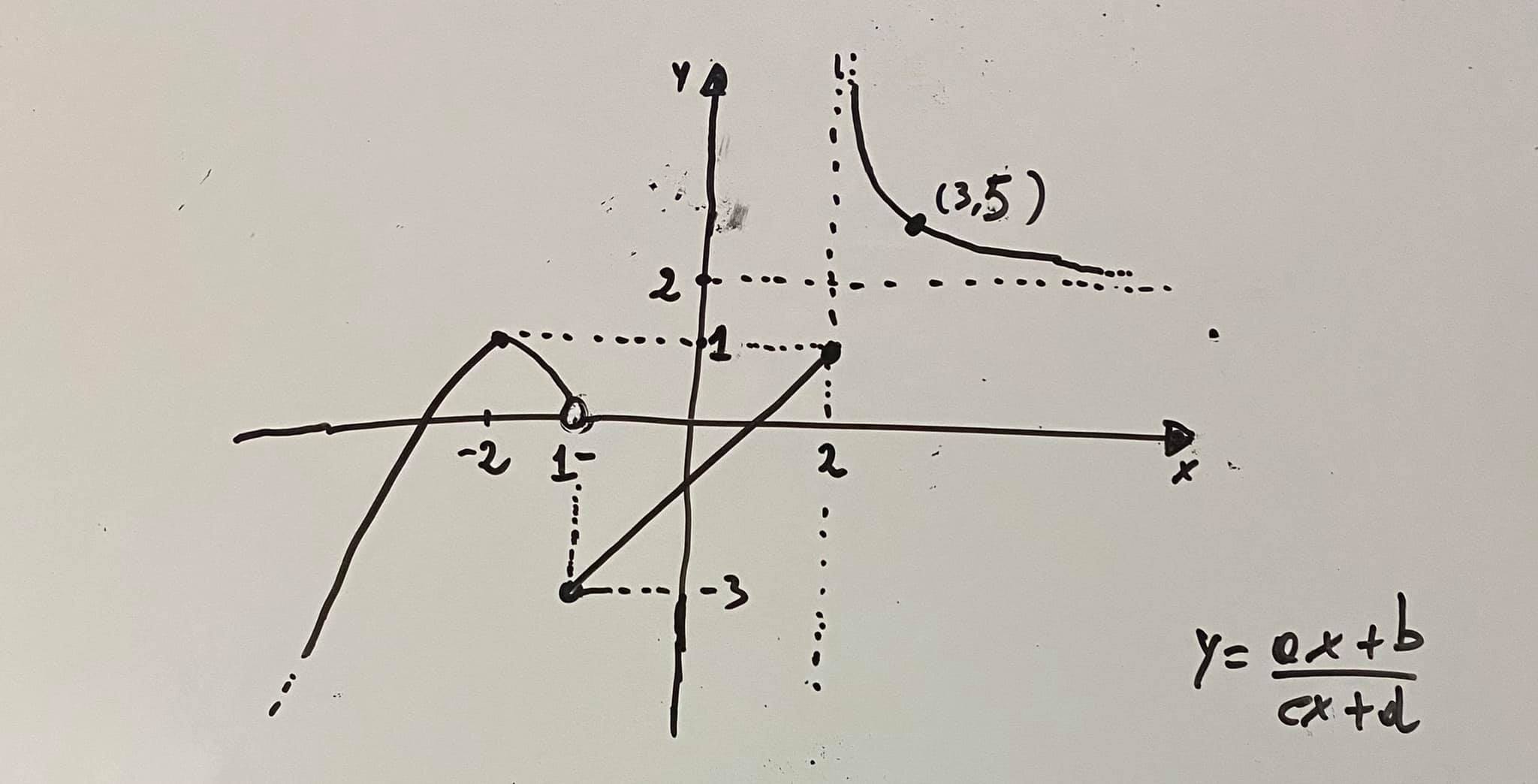
Esempio 1.1.- Il grafico della funzione y = f(x) è rappresentato nella seguente figura. La funzione f(x) ha dominio R è il suo grafico è costituito da tre parti, la prima è un arco di parabola con asse di simmetria parallelo all’asse y, la seconda è un segmento, e la terza da un arco di una funzione omografica.
Determinare:
a) Deduci dal grafico i seguenti limiti:
\[\lim_{x\rightarrow -\infty }f(x), \, \, \lim_{x\rightarrow 1^{-} }f(x),\, \, \lim_{x\rightarrow 1^{+}}f(x),\, \, \lim_{x\rightarrow +\infty }f(x)\]
b) Scrivi l’espressione analitica di f(x);
c) Deduci le immagini di x = -2, x = 2, x = -1 e le controimmagini di y = 1 e y = 5;
d) Determina l’insieme immagine, Img (f), della funzione;
e) Verifica con la definizione il limite $\displaystyle \lim_{x\rightarrow +\infty }f(x)$;
f) Stabilire i valori di x per i quali la funzione si annulla, è positiva ed è negativa.
Risoluzione
Risolviamo il punto b). Il ramo parabolico della curva si può determinare tenendo conto che la parabola ha il vertice nel punto V(-2,1) e passa per il punto (-3,0), il che si deduce per la simmetria della parabola rispetto all’asse x = – 2 e dal fatto che …
Quindi l’equazione dell’arco di parabola sarà del tipo $\displaystyle y=ax^{2}+bx+c$ e dovendo avere il vertice di ascissa -2 e ordinata 1 si ricavano le relazioni \[-\frac{b}{2a}=-2,\, \, 1=4a-2b+c\]
Inoltre, dal passaggio dell’arco di parabola per il punto (-3,0) si ottiene l’ulteriore relazione \[0=9a-3b+c\]
e mettendo a sistema le relazioni trovate si ha:
\[\left\{\begin{matrix} -\frac{b}{2a}=-2 & \\ 1=4a-2b+c& \\ 0=9a-3b+c& \end{matrix}\right.\]
Risolto tale sistema si ottiene a = -1, b = -4 e c = -3, da cui l’arco di parabola ha equazione:
\[y=-x^{2}-4x-3,\, \, \, \, \, con\, \, \, x<-1\]
Per quanto riguarda il segmento aventi per estremi i punti (-1, -3) e (2, 1) basta applicare la formula dell’equazione di una retta passante per due punti… e si ha: \[y=\frac{4}{3}x-\frac{5}{3}\]
Infine, per la funzione omografica, la cui equazione è del tipo $\displaystyle y=\frac{ax+b}{cx+d}$, procediamo nel seguente modo:
- dato che ha asintoto verticale x = 2 deve aversi per x = 2: $\displaystyle 2c+d=0$
- dato che ha asintoto orizzontale y = 2 deve aversi: $\displaystyle \frac{a}{c}=2$
- e dato che passa per il punto (3,5) deve aversi: \[5=\frac{3a+b}{3c+d}\]
Pertanto risolvendo il sistema \[\left\{\begin{matrix} 2c+d &=0 \\ \frac{a}{c} &=2 \\ 5 & =\frac{3a+b}{3c+d} \end{matrix}\right.\]
con la scelta c = 1 si ottiene: \[a=2,\, \, b=-1,\, \, c=1,\, \, d=-2\]
Infine l’espressione analitica della funzione è:
\[f(x)=\left\{\begin{matrix} -x^{2}-4x-3&\, \, se\, \, x<-1 \\ \frac{4}{3}x-\frac{5}{3} &\: \: se\, \, -1\leq x\leq 2 \\ \frac{2x-1}{x-2}&\: \: se\, \, x>2 \end{matrix}\right.\]
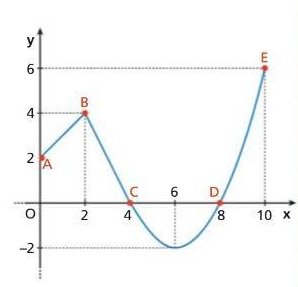
Esempio 1.2.- Il grafico della funzione y = f(x) è quello rappresentato nella figura 1.
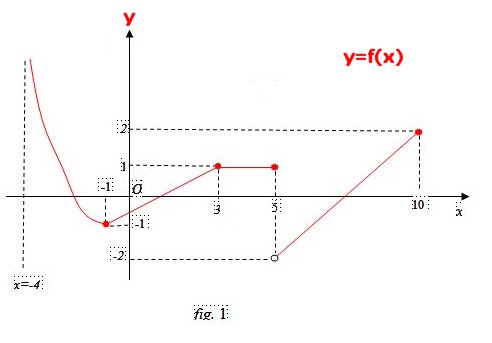
Determinare:
a) il dominio D e il codominio di f(x);
b) l’insieme soluzione dell’equazione f(x) = 0;
c) l’insieme soluzione della disequazione f(x) > 0, e della disequazione f(x) < 0;
d) gli intervalli in cui f(x) è strettamente crescente e strettamente decrescente;
e) f(-1), f(4), f(10), f -1 (1), f -1 (2);
f) la controimmagine di y = 1,5 è compreso tra x = 5 e x = 10?
g) E’ vero che il valore massimo della funzione è 2? Qual è il valore minimo della funzione?
h) E’ vero che la retta x = – 4 è un asintoto verticale?
i) Esiste un sottoinsieme del dominio in cui la funzione è costante?
l) la funzione è iniettiva? E’ suriettiva? E’ biettiva?
m) nel punto x = 5 la funzione è continua?
Risoluzione (vedi foto)
a) Il dominio della funzione è l’intervallo ] – 4, 10 ], mentre il codominio è l’intervallo $\displaystyle \left ( -2,+\infty \right )$ .
b) L’equazione f (x ) = 0 ammette tre soluzioni: x = a, x = b, x = c ove a, b, c sono le ascisse dei punti d’intersezione del grafico della curva con l’asse x.
c) f(x) > 0 per – 4 < x < a, b < x < 5, c < x < 10; f(x) < 0 per a < x < b, 5 < x < c, con a, b, c numeri indicai nel punto precedente b);
d) La funzione è strettamente crescente in ] -1, 3 [ e ] 5, 10 [ ; strettamente decrescente in ] – 4, -1 [.
e) f(-1) è l’immagine della funzione per x = -1, tale valore si legge sul grafico in corrispondenza di x = -1 e si ha:
f(-1) = -1;
f(4) non esiste, f(10) = 2,
$\displaystyle f^{-1}\left ( 1 \right )=3,\, \, f^{-1}\left ( 2 \right )=10$
f) Sì
g) NO, la funzione è illimitata superiormente, ovvero il suo estremo superiore è + infinito; la funzione non ammette valore minimo, il suo estremo inferiore è -2.
h) Si
l) Si, la funzione è costante nell’intervallo [ 3, 5 ]
l) NO, la funzione non è iniettiva; Sì, la funzione è suriettiva; No, la funzione non è biettiva perché non è iniettiva.
m) No, infatti il limite sinistro vale 1 e quello destro -2
Esempio 1.3.- Data la funzione: \[f(x)=\left\{\begin{matrix} x-1 &\, se\, x>0\\ x^{2} &\, se\: -1\leq x\leq 0 \\ 2 & se\, \, x<-1 \end{matrix}\right.\]
- rappresentarla graficamente;
- determinare il dominio e il codominio;
- stabilire se è iniettiva e suriettiva;
- stabilire gli intervalli in cui la funzione è strettamente crescente;
- risolvere l’equazione f(x) = 0 e l’equazione f(x) = 4;
- esiste un sottoinsieme del dominio in cui la f(x) è costante?;
- determinare y(2), y(-1/2), y(-12);
- stabilire $\displaystyle f^{-1}\left ( 1 \right ),\: f^{-1}\left ( 2 \right ),\, f^{-1}\left ( 4 \right ),$;
- la funzione è continua nel punto $\displaystyle x_{0}=4$ ? e in $\displaystyle x_{0}=0$ ?
- in $\displaystyle x_{0}=-1$ la funzione è continua o discontinua?
Esempio 1.4.- Nella figura sottostante è rappresentata una funzione g(x) = f'(x). I tratti AB e BC sono segmenti di retta, il tratto CDE appartiene ad una parabola con asse di simmetria parallelo all’asse y, e in C la funzione g(x) è derivabile. a) Sapendo che f(0) = 0, calcolare f(2) e f(4), quindi tracciare un grafico probabile della funzione f(x); b) Ricavare l’espressione analitica di g(x), quindi calcolare f(8) e f(10); c) Calcolare il volume del solido generato dalla rotazione completa attorno all’asse x dell’arco di parabola CD.
Risoluzione ragiornata
Calcolare le equazioni delle rette AB e BC e poi integrare, calcolando le costanti di integrazione. Per il tratto CDE trovare l’equazione della parabola di vertice dato, vedi figura, e passante per un punto, integrare e calcolare la costante d’integrazione. Di conseguenza la funzione f(x) è una funzione definita a tratti…
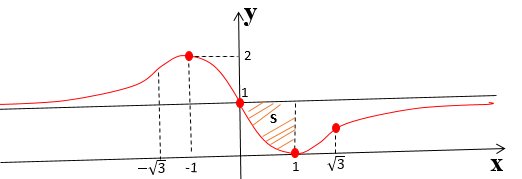
Esempio 1.5.- La funzione f(x), il cui grafico è rappresentato nella figura sottostante, è continua e derivabile in R. Inoltre il suo grafico è simmetrico rispetto al punto (0,1), presenta un flesso $x=\sqrt{3}$ e ammette un asintono orizzontale e l’area S evidenziata vale ln 2.
Determinare:
- Indicata con F la funzione integrale $F(x)=\int_{0}^{x}f(t)dt$ determinare F(0), F(1), F(-1);
- Dedurre l’andamento del grafico della funzione integrale F(x) da quello di f(x), scrivere le equazioni delle rette tangenti al grafico di F(x) nei punti x = 1, x =-1;
- Se come punto iniziale della funzione integrale fosse stata considerata l’ascissa 1 anziché zero come sarebbe cambiato il grafico di F? Determinare in funzione di F(x) l’equazione della funzione integrale $G(x)=\int_{1}^{x}f(t)dt$
- Sapendo che $f(x)=\frac{\left ( x-1 \right )^{2}}{x^{2}+1}$ stabilire se la regione illimitata tra il grafico della f(x) e l’asintoto per $x\geq 1$ ha area finiita.
Risoluzione
(In collaborazione con il prof. Arturo Vallante)
1) F(0) = 0 (ovvio)
F(1) =1-ln2 (si vede calcolando l’area del quadrato di lato 1 che incluse l’area S;
Per simmetria si vede che F(-1) = -1 – ln2
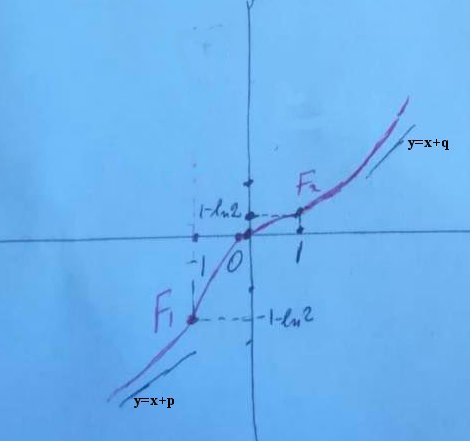
2) Il grafico della funzione integrale è accennato nella seguene figura.
3)Le equazioni delle rette tangenti si ottengono considerando i punti $F_{2}$( 1, 1- ln2) e $F_{1}$(-1, -1-ln2) e applicando ad ognuno l’equazione del fascio di rette di centro un punto. Dunque per il primo punto, per m = f(1) = 0, si ha:
y – (1-ln2) = 0 (x-1) ossia y = 1 – ln2
e al secondo punto, con m = f(-1) = 2, si ha:
y – (-1-ln2) = 2 (x+1) ossia y = 2x + 1- ln2.
Se cambia il punto iniziale la curva ottenuta trasla lungo l’asse y.
4) Calcolo area regione indicata
con H si è indicato l’uso della Regola di l’Hôpital.