 UNA PASQUA MATEMATICA, tratto da un post di Stefano Fortini pubblicato su Facebook.
UNA PASQUA MATEMATICA, tratto da un post di Stefano Fortini pubblicato su Facebook.
“Vi sarà sicuramente capitato di chiedervi perché la Pasqua, a differenza del Natale, non cade sempre lo stesso giorno. La ragione è che la data della Pasqua è stabilita in base al ciclo lunare e, in particolare, cade la prima domenica dopo la prima luna piena che segue l’equinozio di primavera.
Tale regola risale al Concilio di Nicea convocato dall’imperatore Costantino il 20 maggio del 325 d.C., il primo concilio ecumenico cristiano. Dovendo la regola di calcolo essere valida per tutte le popolazioni cristiane della terra, il riferimento non può essere una “luna reale” ma una cosiddetta “luna ecclesiastica”, avente un periodo ben definito e corrispondente, almeno approssimativamente, con il periodo sinodico della Luna reale: questo fu il punto di partenza per l’elaborazione di tutti i metodi che avrebbero permesso di calcolare la data della domenica di Pasqua.
L’astronomo greco Metone, vissuto ad Atene nel V sec. a.C., compì osservazioni fondamentali per lo studio delle lune e, in particolare, scoprì un ciclo di 19 anni (detto “ciclo metonico”) durante il quale avvengono 235 lunazioni (intervallo di tempo tra due lune nuove consecutive), dopo il quale le fasi lunari ritornano nelle stesse date dell’anno.
A queste osservazioni è legato il concetto di numero aureo (o numero d’oro), ovvero un numero che identifica la posizione di un determinato anno all’interno del corrispondente ciclo diciannovennale di Metone. Per formalizzare il calcolo del numero aureo (e di altri numeri di cui parlerò in seguito) è necessario definire la funzione modulo.
La funzione modulo, indicata con mod e applicata a due numeri, è una funzione che dà come risultato il resto della divisione del primo numero per il secondo. Ad esempio:
mod(7, 5) = 2
perché 7 : 5 = 1 resto 2.
Per calcolare il numero aureo di un determinato anno è necessario inoltre specificare il primo anno di un ciclo. Questo fu selezionato dal monaco cristiano Dionigi il Piccolo, ricordato per aver collocato la nascita di Gesù nell’anno 753 “ab urbe condita”, cioè dalla fondazione di Roma e per aver introdotto il computo degli anni a partire da tale data.
Una peculiarità della numerazione di Dionigi è che non contempla l’anno zero: il monaco, infatti, non conosceva lo “zero”, introdotto in Europa nel 1202 da Leonardo Fibonacci con il suo Liber Abbaci. Egli stabilì quindi che al 31 dicembre dell’1 a.C. seguisse direttamente il 1° gennaio dell’1 d.C. e fissò nell’1 a.C. tanto la natività quanto il primo anno del ciclo.
Segue che il numero aureo A di un qualunque anno N d.C. è dato da
A = 1 + mod(N, 19)
Ad esempio, il numero d’oro dell’anno 2023 è A = 1 + mod(2023, 19) = 1 + 9 = 10 perché 2023 : 19 = 106 con resto 9.
Il calcolo della data di Pasqua veniva effettuato utilizzando apposite tabelle denominate “almanacchi lunari”, all’interno delle quali venivano evidenziate le 235 lune nuove ecclesiastiche, ed utilizzando il numero aureo. Il calcolo, giù piuttosto complesso, divenne ancora più ingarbugliato in seguito alla riforma del calendario del 1582, ovvero quando entrò in vigore il calendario gregoriano (ancora oggi utilizzato in quasi tutto il mondo) in sostituzione del calendario giuliano.
Fu il grande matematico Carl Friedrich Gauss ad elaborare un algoritmo che permette, conoscendo semplicemente l’anno (ad esempio 2023), di calcolare la data della Pasqua. Pubblicato sulla rivista “Monatliche Correspondenz” nel 1800 con il titolo “Berechnung des Osterfestes” (“Calcolo della Pasqua”) e corretto dallo stesso Gauss nel 1816, l’algoritmo può essere sintetizzato come segue.
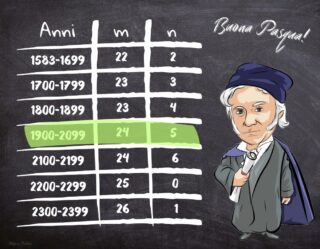
Nella tabella in figura sono evidenziati i valori di due parametri, indicati con m e n, che serviranno per il calcolo della Pasqua. Indicando con N l’anno di cui si vuole calcolare la Pasqua, occorre calcolare cinque parametri (indicati con a, b, c, d, e), per i quali è necessaria ancora una volta la funzione modulo introdotta in precedenza. I parametri possono essere calcolati come segue:
a = mod(N, 19)
b = mod(N, 4)
c = mod(N, 7)
d = mod(19a + m, 30)
e = mod(2b + 4c + 6d + n, 7)
Si noti che il parametro a può essere anche visto anche come il numero aureo diminuito di 1, ovvero a = A – 1. Ora, se d + e ≤ 9, allora la Pasqua cade il giorno (d + e + 22) del mese di marzo, se invece d + e > 9 la data sarà il giorno (22 + d + e – 31) del mese di aprile.
Esistono soltanto due eccezioni: se la data risultante dalla formula è il 26 aprile, allora la Pasqua cade il 19 aprile, mentre se si ottiene il 25 aprile e contemporaneamente d = 28 e a > 10 allora la data effettiva sarà il 18 aprile.
Adesso siamo pronti per calcolare la data della Pasqua del 2023:
N = 2023
Dalla tabella sappiamo che m = 24 e n = 5. Pertanto:
a = mod(2023, 19) = 9
perché 2023 : 19 = 106 con resto 9.
b = mod(2023, 4) = 3
perché 2023 : 4 = 505 resto 3.
c = mod(2023, 7) = 0
perché 2023 : 7 = 289 resto 0.
d = mod(19a + m, 30) = mod(19 · 9 + 24, 30) = mod(195, 30) = 15
perché 195 : 30 = 6 resto 15.
e = mod(2b + 4c + 6d + n, 7) = mod(2 · 3 + 4 · 0 + 6 · 15 + 5, 7) = (101, 7) = 3
perché 101 : 7 = 14 resto 3.
Siccome d + e = 15 + 5 = 18 > 9, la Pasqua cade il giorno 22 + d + e – 31 di aprile, ovvero il 22 + 18 – 31 = 9 di aprile.”
Vedere anche articolo pubblicato su www.matematicamente.it
