Esempio 1.- Dal totale alla parte. Calcolare i 3/4 di 28.
Rioluzione
Bisogna moltiplicare 28 per 3/4, ossia:
28 x 3/4 = 7 x 3 = 21
Possiamo indicare questo problema come il calcolo di una parte del totale e impostarlo schematicamente così:
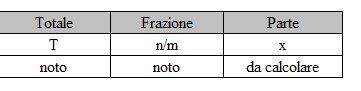
x = T x n/m
Nell’esempio 1 il totale è T = 28 e la frazione è n/m = 3/4, mentre la parte da calcolare è x = 21, cioè 21 è i 3/4 di 28. Questo problema “Dal totale alla parte” lo possiamo anche chiamare problema diretto con le frazioni, mentre si chiama problema inverso quando si conosce la parte e si vuole calcolare il totale.
Esempio 2.- Dalla parte al totale. Sapendo che 36 è i 3/4 di una data quantità, calcolare la quantità.
Risoluzione
Bisogna moltiplicare 36 per 4/3, inverso della frazione 3/4, ossia:
x = 36 x 4/3 = 12 x 4 = 48
Possiamo indicare questo problema come schematicamente così:
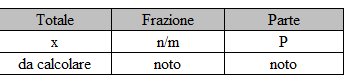
x = P x m/n
Esempio 3.- Sapendo che un negozio vende 30 bottiglie di Rum su 150 bottiglie di alcolici vendute calcolare la frazione e la percentuale di bottiglie di Rum vendute.
Risoluzione
Bisogna fare il rapporto tra il numero delle bottiglie di Rum vendute e il numero totale
di bottiglie vendute:
x = 30 / 150 = 1/5
il che ci indica che sul totale di 150 bottiglie, inteso come 1, 1/5 risultano quelle di Rum vendute. Per sapere la percentuale di bottiglie vendute basta eseguire la divisione 1/5 e moltiplicare il risultato per 100:
1/5 x 100 = 0,2 x 100 = 20%
e ciò indica che su 150 bottiglie vendute 30 sono di Rum.
Possiamo indicare questo problema come schematicamente così:
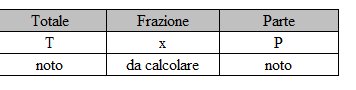
frazione: x = P / T
percentuale: x = P / T x 100
Questi tre tipi di problemi sono alla base di problemi più complessi con le frazioni.
Esempio 4.- Un rivenditore di automobili vende in un anno 273 auto di tre marche differenti (Fiat, Mercedes, Renault). Sapendo che 1/3 sono Fiat, 2/7 sono Mercedes calcolare il numero di Renault vendute.
Possiamo procedere in due modi differenti.
Primo Metodo.- Schematizziamo il problema con un rettangolo, ossia immaginiamo che il parco auto vendute sia rappresentato come nella seguente figura:

Indicando tutto il parco auto vendute con 1, il totale in senso frazionario, e tenuto conto che le Fiat vendute sono 1/3 del totale e le Mercedes 2/7 si ricava che le Renault vendute sono
1 – (2/7 + 1/3 ) = 8/21 del totale.
Quindi il numero di Renault (parte) sono 8/21 del totale (T) e si possono calcolare con la formula del problema diretto:
R = 273 x 8 / 21 = 13 x 8 = 104
Secondo metodo.- Sapendo che il parco auto vendute è di 273 calcoliamo preliminarmente il numero di Fiat e Mercedes vendute. Si ha:
F = 273 x 1/3 = 91
M = 273 x 2/7 =78
Di conseguenza il numero di Renault vendute è:
R = Totale auto vendute – (F + M) = 273 – (91 + 78) = 104.
Esempio 5.- Un tale percorre in tre giorni 290 km. Sapendo che il secondo giorno percorre 11/12 del primo giorno e che il terzo giorno percorre 6/11 del secondo, determinare quanto percorre il primo giorno.

Risoluzione
Sia AB il percorso del primo giorno, BC quello del secondo giorno e CD quello del terzo giorno.
Indichiamo con AB = 1 il percorso fatto il primo giorno. Di conseguenza il percorso fatto il secondo giorno sarà CD = 11/12, mentre il percorso fatto il terzo giorno sarà CD = (6/11) x (11/12) = 1/2.
Pertanto tutto il percorso in termini frazionari è:
AB = 1 + 11/12 + 1/ 2 = 29/12.
Sapendo che tutto il percorso è di 290 km possiamo calcolare la lunghezza di AB così:
AB = 290 x 12/29 = 10 ´ 12 = 120 km.
