In questa pagina propongo alcuni esercizi sulla scomposizione dei polinomi.
I polinomi assegnati dall’esempio 6.1 sono da considerarsi esercizi di riepilogo e quindi adatti a tutti coloro che hanno già studiato i casi elementari. I casi elementari, o di base, sono presentati negli esempi precedenti 1-5.
Per scomporre un polinomio si può utilizzare la seguente applicazione:
Esempio 1.1.- Raccoglimento totale- Scomporre i seguenti polinomi \[x^{3}y^{5}-\frac{1}{2}x^{2}y^{6}z+2x^{8}y^{3}z^{2}\]
\[-a^{2}b^{3}-\frac{3}{5}ax^{6}b^{6}+3a^{5}b^{3}c^{3}\]
Esempio 2.1.- Raccoglimento parziale- Scomporre il seguente polinomio \[t^{2}+tx+ty+yx\]
Risoluzione
\[t^{2}+tx+ty+yx=t\left ( t+x \right )+y(t+x)=(t+x)(t+y)\]
Esempio 2.2.- Scomporre il polinomio \[6a^{2}b-4a^{2}b^{2}-6ab^{3}+9ab^{2}\]
Risoluzione
\[6a^{2}b-4a^{2}b^{2}-6ab^{3}+9ab^{2}=ab\left ( 6a-4ab-6b^{2}+9b \right )\]
da cui
\[ab\left [ 2a\left ( 3-2b \right )+3b(3-2b) \right]\]
\[ab\left [ \left ( 3-2b \right )\left ( 2a+3b \right ) \right ]=ab(3-2b)\left ( 2a+3b \right )\]
In pratica abbiamo prima raccolto a fattor comune ab e poi nella parentesi tonda applicato il raccoglimento parziale.
Esempio 3.1.- Differenza di due quadrati e metodi basati sui prodotti notevoli.- Scomporre i seguenti polinomi
\[4x^{2}-16,\, \, \, 8x^{3}-27,\, \, \, -x^{2}+2x-1,\, \, x^{2}-7x+10\]
Non sai scomporlo? Allora vedi il mio video sul mio canale Youtube
Nota.- Il quarto polinomio non si può scomporre con il metodo dei prodotti notevoli ma come trinomio speciale, vedi esempio 4,1
Esempio 3.2.- Scomponi il polinomio \[4y^{2}-x^{2}+2x-1\]
Non sai scomporlo? Allora vedi il mio video sul mio canale Youtube
Esempio 4.1.– Trinomio particolare di secondo grado.- Scomponi i polinomi \[x^{2}-5x+6,\, \, x^{2}-7x+12,\, \, x^{2}-13x+36,\, \, x^{2}+x-20\]
\[6x^{2}-x-1\]
\[3x^{2}-5x+2,\, \, 5x^{2}-7x+2,\, \, 12x^{2}-13x+1\]
Non sai scomporlo? Allora vedi il mio video sul mio canale Youtube
NOTA.- Per gli studenti del secono anno superiore.- Il trinomio speciale si può scomporre anche con un altro metodo che si studia al ° Anno della Scuola Superiore. Vedi un video qui
Esempio 5.1– Scomposizione mediante il teorema di Ruffini e la Regola di Ruffini. Scomponi i polinomi \[x^{3}+2x-3\] \[2x^{3}+5x+7\] \[2x^{4}+5x^{2}-3x-46\]
Il primo polinomio si può scomporre con un’applicazione della Regola di Ruffini, infatti ammette come zero x = 1. Si ha: … continua da solo…
Anche il secondo polinomio si può scomporre con la Regola di Ruffini, infatti ammette come zero x = -1. Si ha: \[2x^{3}+5x+7=(x+1)\left ( 2x^{2}-2x+7 \right )\]
Esempio 6.1.- Applicazione di due o più metodi.- Scomporre in fattori i seguenti polinomi \[x^{3}-x,\, \, 4x^{2}-4x+1,\, \, x^{4}+4y^{2}+9z^{6}-4x^{2}y+6x^{2}z^{3}-12yz^{3}\]
\[x^{3}-6x^{2}+12x-8,\, \, x^{2}-x-20,\, \, 4m^{4}x^{2}-4n^{4}x^{2}+3m^{4}y^{2}-3n^{4}y^{2}\]
Se non sai scomporli prova a vedere il mio video su Youtube
Esempio 7.1- Scomposizioni più complicate.- Scomporre i seguenti polinomi \[x^{2}-4y^{2}-x+2y\]
\[a^{2}+4ab+4b^{2}-a-2b\]
\[c^{2}-a^{2}+6ab-9b^{2}+c-a+3b\]
\[a^{2}-y^{2}-4xy-4x^{2}+a+2x+y\]
Se non sai scomporli prova a vedere il mio video su Youtube
Esempio 7.2.- Scomporre i seguenti polinomi: \[x^{2}-4y^{2}-x^{3}-8y^{3}\]
\[x^{5}-xy^{4}-x^{4}y+y^{5}\]
\[x^{4}-y^{4}+2x^{3}y-2xy^{3}\]
\[z^{6}+z^{4}-2z^{5}-z^{2}+2z-1\]
Se non sai scomporli prova a vedere il mio video su Youtube
Esempio 7.3.- Scomporre i polinomi \[a^{3}-b^{3}-9a+9b+a^{2}b-ab^{2}\]
\[ax^{2}+ax-2a-bx^{2}-bx+2b\]
\[x^{6}+y^{6}-x^{4}-2x^{2}y^{2}-y^{4}\]
\[a^{2}-5ab+4b^{2}+a^{3}-a^{2}b\]
Se non sai scomporli prova a vedere il mio video su Youtube
Esempio 7.4.- Scomporre il polinomio \[x^{2}-14x+6+x^{3}\] utilizzando la Regola di Ruffini
Risoluzione
Noi qui utilizziamo una procedura diversa dalla Regola di Ruffini.
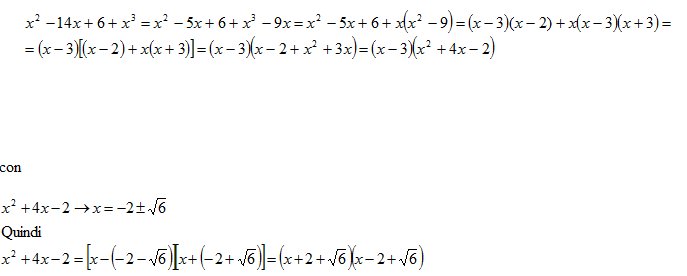
Esempio 7.5.- Scomporre il polinomio \[x^{8}+x^{4}+1\]
