- Dominio D della funzione;
- Simmetrie e periodicità della funzione;
- Positività della funzione;
- Intersezioni con gli assi;
- Limiti ed asintoti;
- Derivata prima per determinare i punti di massimo e di minimo relativi e i flessi a tangente orizzontale;
- Derivata seconda per determinare i flessi della funzione e la convessità;
- Eventualmente si possono determinare alcuni punti della funzione.
Di fondamentale importanza sono i punti 1), 5) e 6), grazie ai quali spesso si può già accennare il grafico della funzione.
Esempio 1.1.- Funzioni razionali intere. Studiare la funzione e disegnarne il grafico \[y=x^{3}-7x^{2}-4x+10\]
Se non la sai studiare consulta il mio video su Youtube
Esempio 1.2.- Studiare la seguente funzione e disegnare il grafico \[y=3x^{2}-x^{3}\]
Se non sai fare l’esercizio prova a vedere il mio video su Youtube
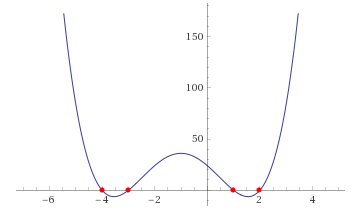
Esempio 1.3.- Studiare la funzione \[y=x^{4}+4x^{3}-7x^{2}-22x+24\] Il grafico è indicato nella seguente figura.
Esempio 1.4.- Studiare la funzione e disegnarne il grafico \[f(x)=\left\{\begin{matrix} x+3 &\, \, \, se\, \, \, \, x\geq 2 \\ x^{2} &\, \, \, se-2<x<2 \\ -4 & se\, \, x\leq -2 \end{matrix}\right.\]
Se non sai studiare tale funzione vedi il mio video su Youtube
Esempio 2.1.- Funzioni razionali fratte. Studiare la funzione e disegnarne il grafico \[y=\frac{x^{3}}{x^{2}-4}\]
Se non la sai studiare prova a vedere il mio video su Youtube
Esempio 2.2 .- Studiare la funzione e disegnarne il grafico \[y=\frac{x^{2}}{x+1}\]
Esempio 6.- Studiare le funzioni e disegnarne il grafico \[y=ln\left ( x^{2}+5x-6 \right )\]
y =ln |3 -2lnx|
\[y=\frac{x^{2}}{16}\left(4ln^{2}\frac{x}{4}-10ln\frac{x}{4}+5\right)\]
Esempio 7.- Studiare la funzione e disegnarne il grafico\[y=\frac{e^{x}-2}{x}\]
Non sai studiare queste tre (5, 6, 7) funzioni? Allora prova a vedere come ho fatto io. (completamente svolte)…
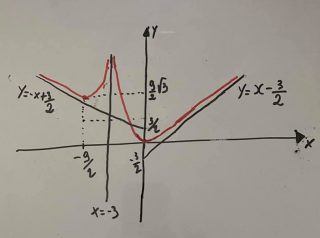
Esempio 8.1.- Studiare la seguente funzione e accennare il grafico \[f(x)=\sqrt{\frac{x^{3}}{x+3}}\]
Per determinare il dominio D della funzione occorre richiedere che il radicando sia maggiore o uguale di zero, ossia \[\frac{x^{3}}{x+3}\geq 0\]
Si ha \[x^{3}\geq 0\Rightarrow x\geq 0,\, \, \, \, x+3>0\Rightarrow x>-3\] e dunque il dominio è \[D=(-\infty ,-3)\cup [0,+\infty )\]
La funzione è sempre positiva e si annulla in x =0; inoltre ammette un asintoto verticale x = -3 e un asintoto obliquo y = x – 3/2 a più infinito e uno a meno infinito d’equazione y = – x + 3/2.
La derivata prima è \[f'(x)=\frac{1}{2\sqrt{\frac{x^{3}}{x+3}}}\frac{3x^{2}(x+3)-x^{3}}{\left ( x+3 \right )^{2}}=\frac{x^{2}\left ( 2x+9 \right )}{2\left ( x+3 \right )^{2}\sqrt{\frac{x^{3}}{x+3}} }\] e la funzione ammette due minimi in x = 0 e x = – 9/2. Il grafico della funzione è riportato nella figura
Esempio 8.2.- Studiare le seguenti due funzioni \[y=\sqrt{x^{2}-10x},\, \, y=\sqrt{x-x^{2}}-x,\: \: y=\frac{x+1}{\sqrt{2x^{2}+x-1}}\]
Esempio 9. Studiare la seguente funzione e tracciare il grafico \[y=\frac{e^{x}}{x^{2}-2}\]
Se non la sai studiare provare a vedere il mio video su Youtube
Esempio 10. Studiare la seguente funzione e tracciare il grafico \[y=\left ( x+1 \right )e^{1-x}\]
Se non la sai studiare provare a vedere il mio video su Youtube
Esempio 11. Studiare la seguente funzione e tracciare il grafico \[y=\frac{\sqrt{x+1}}{e^{x}}\]
Se non la sai studiare prova a vedere il mio video su Youtube
Esempio 12.- Studiare la seguente funzione e tracciare il grafico \[y=e^{x^{2}}+1\]
Se non sai cosa fare prova a vedere il mio video su Youtube
Esempio 13.- Studiare la seguente funzione e accennare il grafico \[y=log\left ( \pi +e^{-x^{2}} \right )\]
Se non lo sai fare prova a vedere il mio video su Youtube
Studiare inoltre le funzioni \[y=ln\frac{\left ( x-2 \right )^{2}}{x}, y=ln\frac{\sqrt{x}}{x-\sqrt{x}}\]
\[y=ln\frac{x+5}{2x}\]
Quest’ultima funzione ha per dominio \[\left ( -\infty ,-5 \right )\cup \left ( 0+\infty \right )\], la funzione è positiva per 0<x<5 e negativa per x <-5, x>5, interseca l’asse x nel punto (5,0). Inoltre, ammette due asintoti verticali x = 0, x = -5 e un asintoto orizzontale di equazione y = – ln2. La derivata prima è \[y’=\frac{-5}{ x^{2}+5x }\]
Non ti resta che disegnare il grafico…
Esempio 14.- Studiare la seguente funzione e accennare il grafico\[f(x)=\sqrt{x^{3}-4x^{2}}\]
Per determinare il dominio D della funzione occorre richiedere che il radicando sia maggiore o uguale di zero, ossia \[x^{3}-4x^{2}\geq 0\] ed è definita in \[D=\left \{ 0 \right \}\cup [4,+\infty )\] e positiva o nulla nel dominio, si annulla in x = 0 e x = 4. La derivata prima è \[f'(x)=\frac{x\left ( 3x-8 \right )}{2\sqrt{x^{3}-4x^{2}}}\] e la funzione ammette un minimo assoluto nel punto x = 4.
Esempio 15.- Studiare le seguenti funzioni e accennare il grafico\[f(x)=\frac{e^{x}+1}{e^{x}-1}\]
\[y=\frac{2^{x}-4}{2-2^{x}}\]
Esempio 16.- Studiare la seguente funzione e accennare il grafico\[f(x)=1+\sqrt{\frac{x}{e^{x}}}\]
Non sai studiare la funzione? Allora vedi il mio video su Youtube
Esempio 17.- Studiare la seguente funzione e accennare il grafico\[f(x)=(x+1)e^{\frac{x}{x-1}}\]
Esempio 18.- Studiare la seguente funzioni e accennare il grafico\[f(x)=120x^{2}e^{-\left | x \right |}-1\]
Esempio 18.1.- Studiare la seguente funzioni e accennare il grafico
\[ y=sen(2x)cosx,\, x\in \left [ 0,2\pi \right ]\] \[ y=\frac{2senx-1}{cos^{2}x-1}\]
\[ y=senx+\sqrt{3}cosx-2,\, \, x\in \left [ -\pi ,\pi \right ]\]
Esempio 18.2.- Studiare la seguente funzioni e accennare il grafico
\[y=e^{sen\, x},\, \, in\, \, \left [ 0,2\pi \right ]\] \[y=e^{cos\, x},\, \, in\, \, \left [ 0,2\pi \right ]\]
Esempio 19.- Studiare le seguenti funzioni e accennare il grafico \[y=ln\left ( 1-sen\, x \right ),\, \, y=ln\left ( 1-cos\, x \right )\]
\[y=ln\left ( 1-tan\, x \right ),\, \, y=ln\left ( 1-cot\, x \right )\]
Se non sai studiare queste funzioni prova a vedere il mio video su Youtube
Esempio 20.- Studiare la seguente funzione e accennare il grafico\[f(x)=2x-arcsenx\]
\[y=ln\left ( \frac{\pi }{3}-arcsen\, x \right )\] \[y=ln\left ( \frac{\pi }{4}-arc\,cos\, x \right )\]
\[y=ln\left ( \frac{\pi }{6}-arctan\, x \right )\]
Esempio 21.- Studiare la seguente funzione e accennare il grafico\[f(x)=ln(1+2sen^{2}x)\]
Esempio 22.- Studiare la seguente funzione e accennare il grafico\[f(x)=ln\left ( \sqrt{5}+e^{-x^{2}} \right )\]
Esempio 23.- Studiare la seguente funzione e accennare il grafico\[f(x)=(x^{2}+2x)e^{x}\]
Esempio 24.- Studiare la seguente funzione e accennare il grafico \[f(x)=4+e^{\sqrt{x}}-\sqrt{x}\]
Esempio 25.- Studiare la seguente funzione e accennare il grafico\[f(x)=-ln(senx)\]
Esempio 26.- Studiare la seguente funzione e accennare il grafico\[f(x)=6xe^{\frac{1}{x}}\]
Esempio 27.- Studiare la seguente funzione e accennare il grafico\[f(x)=\sqrt{x+1}-\sqrt{x}\]
Esempio 28.- Studiare le seguenti funzioni e accennare \[y=ln\left | 3-2lnx \right |\]
\[y=log_{\frac{1}{2}}\left | 1-2^{x} \right |\]
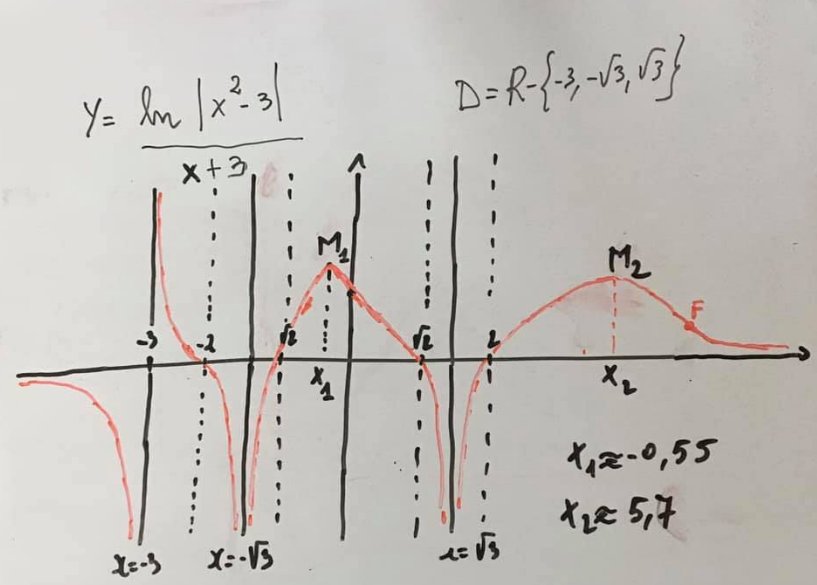
Esempio 29.- Studiare la seguente funzione e accennare \[y=\frac{ln\left | x^{2}-3 \right |}{x+3}\]
La derivata prima non si può studiare elementarmente e quindi il grafico sarà un grafico probabile, ma che somiglia moto a quello reale tracciato in figura. Se vuoi vedere tutto lo svolgimento, e farci un piccolo regalo, clicca qui.